Число степеней свободы.

Понятие идеального газа.

Идеальным называется газ, взаимодействие, между молекулами которого пренебрежимо мало и состояние которого описывается уравнением Клапейрона-Менделеева.

Модель идеального газа.

1. Собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда.

2. Между молекулами газа отсутствует силы взаимодействия.

3. Столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Взаимодействие между молекулами всякого газа становится пренебрежимо слабым при малых плотностях газа, при большом разрежении. Такие газы как воздух, азот, кислород, даже при обычных условиях, т.е. при комнатной температуре и атмосферном давлении мало отличаются от идеального газа. Особенно близки к идеальному газу гелий и водород.

Не следует думать, что взаимодействие между молекулами идеального газа вовсе отсутствует. Напротив, его молекулы сталкиваются друг с другом и эти столкновения существенны для установления определённых тепловых свойств газа. Но столкновения проходят настолько редко, что большую часть времени молекулы движутся как свободные частицы.

Именно столкновения между молекулами позволяют ввести такой параметр как температура. Температура тела характеризует энергию, с которой движутся его молекулы. Для идеального газа в равновесных условиях абсолютная температура пропорциональна средней энергии поступательного движения молекул.

Определение. Макроскопической называется система, образованная огромным числом частиц (молекул, атомов). Параметры, характеризующие поведение системы (например, газа), как целого, называется макропараметрами. Например, давление Р, объём V и температура Т газа – макропараметры.

Параметры, характеризующие поведение отдельных молекул (скорость, масса и т.п.) называется микропараметрами.

Число степеней свободы.

Определение. Числом степеней свободы механической системы называется количество независимых величин, с помощью которых может быть задано положение системы в пространстве.

а) Так, положение в пространстве материальной точки полностью определяется заданием трёх её координат (например, декартовых x, y, z или сферических , т.е. число степеней свободы i=3).

б) Система из 2-х жёстко связанных материальных точек (отрезок, их соединяющий, фиксирован 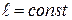). Координаты этих 2-х точек связаны соотношением 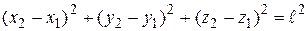, при этом достаточно задать 5 координат, а шестую можно найти из приведённого соотношения, т.е. i=5. Если точки не связаны между собой жёстко, то число степеней свободы i=6. Изменение даёт ещё одну степень свободы, которая называется колебательной.

Положение системы, состоящей из 2-х жёстко связанных материальных точек (или, например, стержня) можно задать следующим образом: задать 3 координаты центра инерции системы С и 2 угла 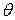и 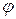, которыми определяется направление в пространстве оси системы (Рис. 7.1).

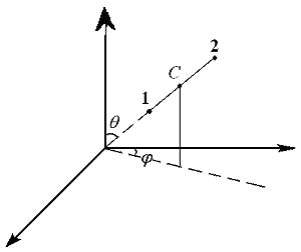
	Первые три степени свободы называется поступательными, а две другие – вращательными. Вращательные степени свободы соответствуют вращению вокруг 2-х взаимно перпендикулярных осей (всего i =5). в) Положение абсолютно твёрдого тела можно определить, задав 3 координаты центра инерции (поступательные степени свободы) и 3 угла (вращательные степени свободы). Т.е.i=6
Рис. 7.1

Закон равнораспределения энергии

В классической статической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: на каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия, равная 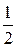кТ. Необходимо отметить, что поступательное и вращательное движения связаны только с кинетической энергией, в то время как колебательное движение связано с наличием и кинетической и потенциальной энергий, причём среднее значение потенциальной и кинетической энергии оказывается одинаковым. Поэтому на каждую колебательную степень свободы приходится в среднем две половинки кТ. Средняя энергия молекулы должна равняться:

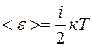
где 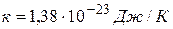(постоянная Больцмана); здесь i – сумма числа поступательных, числа вращательных и удвоенного числа колебательных степеней свободы молекул:

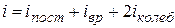
Для молекул с жёсткой связью между атомами i совпадает с числом степеней свободы молекулы.