Внутренняя энергия идеального газа. Число степеней свободы молекулы. Закон равномерного распределения энергии по степеням свободы
Важной характеристикой термодинамической системы является ее внутренняя энергия U – энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц.
К внутренней энергии не относятся кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.
В курсе физики уже встречалось понятие числа степеней свободы i: это число независимых координат, полностью определяющих положение тела (материальной точки, системы материальных точек) в пространстве. Так, например, положение материальной точки определяется тремя координатами (x, y, z), следовательно, i=3. Тонкий стержень имеет 5 степеней свободы (x, y, z, a, b), т.е. 3 поступательные и 2 вращательные, твердое тело имеет 6 степеней свободы (x, y, z, a, b, g), т.е. 3 поступательные и 3 вращательные.
С учетом этого для одноатомных молекул газа (He, Ne, Ar …) i=3, для двухатомных молекул газа (H2, O2, N2 …) с жесткой связью атомов i=5, для трех- и более атомных молекул газа с жесткой связью атомов (CO2, NH3 …) i=6.
Естественно, что жесткой связи между атомами не существует – атомы могут совершать колебания. С учетом этого полное число степеней свободы iå=i+2iколеб. В классической теории рассматривают молекулы с жесткой связью атомов, для них iколеб.=0.
Итак, независимо от числа степеней свободы молекул, три степени свободы всегда поступательные. Ни одна из них не имеет преимущества перед другими, поэтому на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <Wk> [см.(16) в лекции 1,2], т.е.
<Wk>/3 = kT/2.
Важнейший закон классической статистической физики – закон равномерного распределения энергии по степеням свободы – утверждает: на каждую степень свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная kТ/2.
Следовательно, средняя кинетическая энергия молекулы, имеющей i степеней свободы, <Wk> = 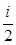 kT . (1)
kT . (1)
Так как в идеальном газе взаимная потенциальная энергия молекул равна нулю (т.е. молекулы между собой не взаимодействуют), то внутренняя энергия U представляет собой кинетическую энергию его молекул.
Для одного моля
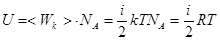 , (2)
, (2)
для произвольной массы m газа
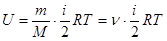 , (3)
, (3)
где М – масса моля, n=m/M – число молей.
Таким образом, внутренняя энергия идеального газа пропорциональна температуре газа и зависит от числа степеней свободы его молекул.
Работа и теплота
Рассмотрим термодинамическую систему, для которой механическая энергия не изменяется, а изменяется лишь ее внутренняя энергия. Внутренняя энергия закрытой системы (т.е. системы, которая не обменивается веществом с внешней средой; в 4,5 лекциях мы изучаем только закрытые системы) может изменяться качественно различными способами:
1. Путем совершения работы внешними телами над системой, например, при сжатии газа температура его повышается и, следовательно, изменяется (увеличивается) его внутренняя энергия.
2. Путем теплообмена, т.е. процесса обмена внутренними энергиями при контакте тел с различными температурами. Энергию, передаваемую от одних тел к другим в процессе теплообмена, называют теплотой.
Таким образом, можно говорить о двух формах передачи энергии от одних тел к другим: работе и теплоте. Энергия механического движения может превращаться в энергию теплового движения и наоборот. При этих превращениях соблюдается закон сохранения и превращения энергии. Применительно к термодинамическим процессам этим законом и является первое начало термодинамики, установленное в результате обобщения многовековых опытных данных.
Дата добавления: 2016-07-27; просмотров: 1989;











