Короткое замыкание цепи с резистором и индуктивностью.

Рассмотрим теперь цепь, питаемую от источника постоянного тока (рис 5.3), в которой после коммутации (замыкания ключа) индуктивность с током [i(0-)№0] оказывается замкнутой на резистор r2.

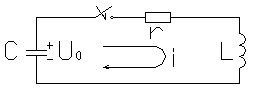Рис 5.3

В образовавшемся при этом контуре благодаря энергии, запасенной в магнитном поле индуктивности, ток исчезает мгновенно: ЭДС самоиндукции, обусловленная убыванием магнитного потока, стремиться поддержать ток в контуре за счет энергии исчезающего магнитного поля. Принужденный ток в данном случае равен нулю, переходной ток в контуре являться свободным, постепенно приближающимся к нулю. Свободный ток удовлетворяет однородному дифференциальному уравнению:

,

общее решение которого

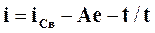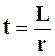, (5.10)

A - постоянная интегрирования, вычисляемая из начальных условий:

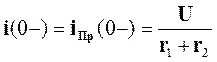(5.11)

где i_Пр(0-) - ток индуктивности в момент, непосредственно предшествующей короткому замыканию. При t=0 из (5.10) имеем:

, т.е. (5.12)

На рис 5.2 изображены графики спада тока и напряжения на индуктивности

(5.13)

С энергетической точки зрения процесс короткого замыкания цепи r, L характеризуется тем, что вся запасенная в индуктивности до коммутации энергия ее магнитного поля

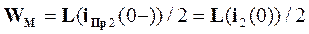
в течении переходного процесса выделяется в резисторе r в виде тепла.