Включение цепи r, L к источнику постоянного напряжения.

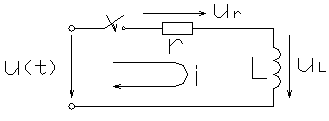Рис 5.1

Рассмотрим включение источника постоянного напряжения u(t)=U в цепь последовательно соединенных r, L элементов (рис 5.1). Для послекоммутационного периода (t>0 и t=0), применив закон Кирхгофа, получим:

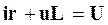(5.4)

а затем составим дифференциальные уравнения рассматриваемой цепи

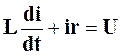(5.5)

полагая uL=L(di/dt)

Решение этого уравнения, согласно (5.3) можно считать известным

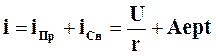(5.6)

Первое слагаемое i_Пр есть частное решение уравнения (5.6) и выражает принужденное (установившееся) значение равное U/r. Второе слагаемое i_Св=Aept представляет собой решение однородного уравнения, т.е. уравнения (5.5) при равенстве нулю правой части. Здесь p и A - соответственно корень характеристического уравнения и постоянная интегрирования. Для рассматриваемой цепи p= -r/L, а постоянная А определяется по начальному току в индуктивности i(0+). Так как ток в индуктивности до момента коммутации отсутствовал (нулевые начальные условия), то при t=0 для полного решения (5.6) имеет место

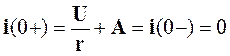(5.7)

Именно здесь проявилось действие закон коммутации (5.1), распространено на полное решение. Окончательно из (5.6) находим, что

,

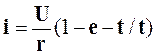где 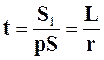- постоянная времени (5.8)

Переходное напряжение на индуктивности можно найти из формулы

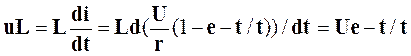
Графики переходного тока и напряжения построенные по формулам (5.8) и (5.9) приведены на рис 5.2.

Чтобы оценить влияние параметров цепи на переходные процесс, свободную составляющую тока i_Св для различных моментов времени, выраженных через t.

Тогда

,

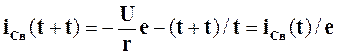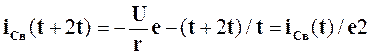
и.т.д.

Следовательно постоянная времени t равна промежутку времени в течении которого свободная составляющая тока убывает в е раз. Практически можно считать, что переходный процесс заканчивается спустя t=(4..5)t.