а) Неплотный индекс

Пусть основной файл F упорядочен по полю ключа К. Построим дополнительный файл FD по следующему правилу:

1) записи файла FD имеют формат FD(K, Р), где К – поле,принимающее значение ключа первой записи блока основного файла F; Р – указатель на этот блок;

2) записи файла FD упорядочены по полю К.

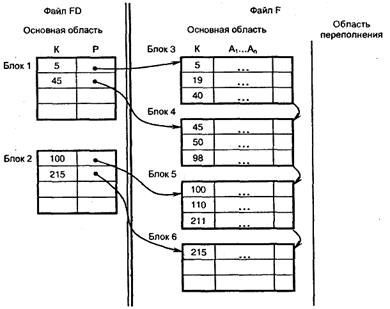
Полученный файл FD называется неплотным индексом. Количество записей файла FD равно количеству блоков основного файла F. Для организации файла FD требуется дополнительная внешняя память.

Поиск вначале выполняется в индексе для нахождения адреса блока основного файла, а за тем этот блок считывает в оперативную память и в нем, например, с помощью последовательного поиска, определяется требуемая запись.

В-дерево. Так как неплотный индекс упорядочен по ключевому полю, то над ним можно построить еще один неплотный индекс (неплотный индекс неплотного индекса) и т.д., пока на самом последнем, верхнем уровне не останется всего один блок.

Полученная структура называется В-деревом порядка т, где т – количество записей в блоке индекса. Такое дерево должно иметь в каждом узле не менее т/2зависимых узлов и все листья должны располагаться на одном уровне.

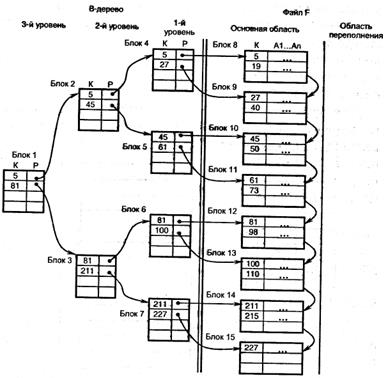
Для осуществления последовательного поиска блоки первого уровня могут быть связаны в цепь по возрастанию значения ключа. Поиск в В-дереве выполняется так же, как и в неплотном индексе. Удачный и неудачный поиск записи в В-дереве требует h обменов, где h – число уровней В-дерева.

При поиске по интервалу значений а ≤ К ≤ b вначале выполняется поиск по К = а в В-дереве, а затем – последовательный поиск по условию К ≤ b в блоках 1-го уровня В-дерева.

Б) Плотный индекс

Пусть по каким-либо причинам невозможно упорядочить основной файл F по ключу К. Построим дополнительный файл FD по правилу:

1) записи файла FD имеют формат FD(K, Р), где К – поле, принимающее значение ключа записи основного файла F; Р – указатель на эту запись;

2) записи файла FD упорядочены по полю К.

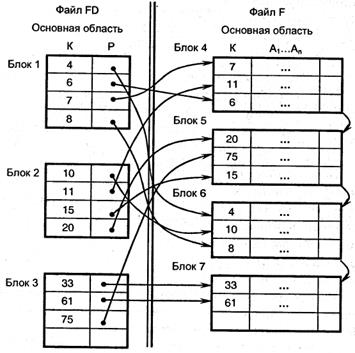
Полученный файл называется плотным индексом. Он строится почти так же, как и неплотный индекс. Различие заключается в том, что для каждого значения ключа К в файле FD имеется отдельная запись, а в неполном индексе - только для значения ключа первой записи блока.

Над плотным индексом можно также построить В-дерево.

Хешированный поиск

Этот метод называется еще методом перемешанных таблиц. Он представляет собой расширение метода прямого доступа на случай отсутствия взаимно однозначного соответствия между ключом и адресом записи. Существует адресная функция (хеш-функция), которая по ключу формирует адрес, однако, не исключено, что один и тот же адрес выделится разным ключам.

Быстродействие обеспечивается заменой переборных и поисковых процедур на прямое вычисление местоположения искомой записи по искомому значению ключа. Вычисление содержит три основных шага:

1) преобразование значения ключа в числовое значение (при нечисловом ключе),

2) хэширование, заключающееся в пересчете числового эквивалента ключа в значение рандомизированной переменной с предположительно равномерным законом распределения. Для пересчета используется выбранная хэш-функция, дающая желаемый эффект рандомизации,

3) масштабирование рандомизированной переменной для приведения получаемых значений к выделенному диапазону адресов памяти (определение адресов в памяти).

Проблемой хэшированного поиска является наличие коллизий, выражающееся получением одинаковых значений адреса хранения записи для различающихся значений ключа. Для решения проблемы коллизий приходится принимать дополнительные меры, такие так выделение дополнительных областей памяти для размещения цепочек перекрывающихся записей.

Этот алгоритм прост, но неэффективен по времени при заполнении таблицы более чем наполовину. Кроме того, при неравномерном распределении ключей этот алгоритм приводит к локальным сгущениям записей и увеличению числа коллизий при относительно свободной таблице.