Закон ослабление рентгеновского излучения

В результате множества процессов, происходящих при взаимодействия рентгеновского излучения с веществом поток излучения ослабляется. Это ослабление можно описать законом Бугера : Ф = Ф_ое^-μd, где Ф - поток излучения, прошедшее через вещество, Ф_о - поток излучения, падающее на вещество, μ – линейный коэффициент ослабления, d – толщина слоя вещества.

Одним из показателей ослабления рентгеновского излучения с веществом является толщина слоя половинного поглощения, которое можно определить из условия, что прошедший через вещество поток излучения равен половине падающего: Ф = Ф_о/2. Если подставить сюда математическое выражение закон Бугера получится: Ф_о/2 =Ф_ое^-μd ½ = е^-μd

ln1 – ln2 = -μd_1/2 d_1/2 = ln2/μ = 0,693/ μ, т.е. толщина слоя половинного поглощения величина обратная линейному коэффициенту ослабления.

Линейный коэффициент ослабления μ можно представить как сумму коэффициентов ослабления первичных действии: когерентного μ_кр и некогерентного μ_нр рассеянии и фотоэффекта μ_{ф :} μ = μ_кр + μ_нр + μ_ф.

Поток рентгеновского излучения ослабляется пропорционально числу атомов вещества, через которое этот поток проходит. Чем больше атомов в единице длины вещества, соответственно в единице объема, тем сильнее ослабляется поток рентгеновского излучения. Отсюда следует, что линейный коэффициент ослабления зависит от плотности вещества ρ μ = ρμ_m, где μ_m – массовый коэффициент ослабления, который зависит от природы вещества и от длины волны излучения..

Используя массовый коэффициент ослабления, закон Бугера можно представить в виде .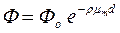

Одним из показателей ослабления рентгеновского излучения с веществом является толщина слоя половинного поглощения, которое можно определить из условия, что прошедший через вещество поток излучения равен половине падающего: Ф = Ф_о/2. Если подставить сюда математическое выражение закон Бугера получится: Ф_о/2 =Ф_ое^-μd ½ = е^-μd

ln1 – ln2 = -μd_1/2 d_1/2 = ln2/μ = 0,693/ μ, т.е. толщина слоя половинного поглощения величина обратная линейному коэффициенту ослабления.