Уравнение Бернулли для сжимаемого газа
Рассмотрим полную энергию секундного массового расхода газа.
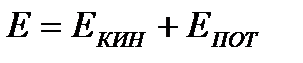 =
= 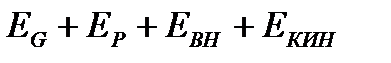 ,
,
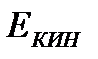 =
= 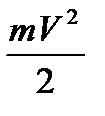 ;
; 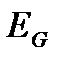 = const;
= const; 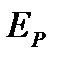 =
= 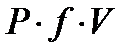
Для сжимаемого газа плотность в разных сечениях струйки будет разной, следовательно, будет разной и температура согласно уравнению состояния газа
(P= 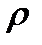 RT). Поэтому по сравнению с несжимаемым газом для сжимаемого газа необходимо учитывать изменение внутренней энергии вдоль струйки, т.к. внутренняя энергия является функцией температуры.
RT). Поэтому по сравнению с несжимаемым газом для сжимаемого газа необходимо учитывать изменение внутренней энергии вдоль струйки, т.к. внутренняя энергия является функцией температуры.
Из термодинамики известно, что внутренняя энергия 1 кг газа при нагревании его до температуры Т определяется по формуле:
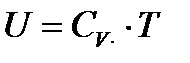 ,
,
Тогда Евн массы газа m равна:
Евн=U  m=C
m=C 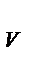 T
T  m;
m;
Из уравнения состояния газа (P= 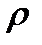 RT)
RT)
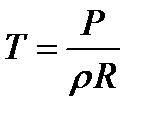 ,
,
Евн = Cv 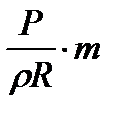 =
= 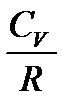
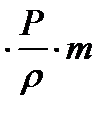 =
= 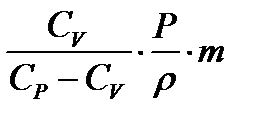 =
= 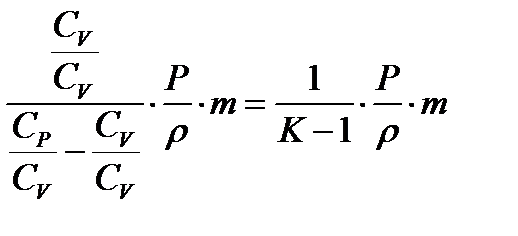 ;
;
Подставим в уравнение постоянства энергии формулы для определения всех видов энергии:
Екин + 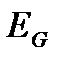 + Е
+ Е 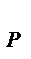 + Е
+ Е 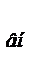 = const;
= const;
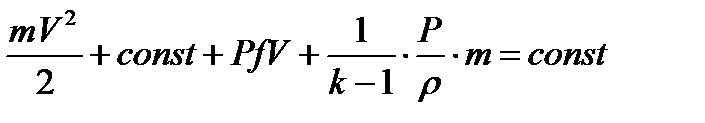 ,
,
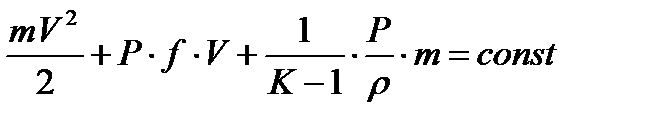 ;
;
Разделим все части уравнения на m:
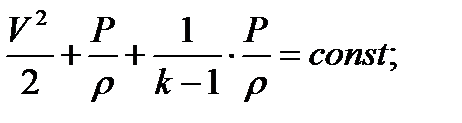
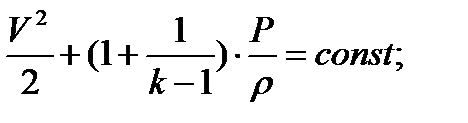
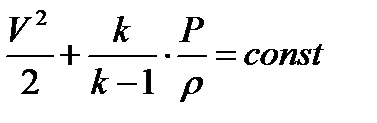 .
.
Уравнение Бернулли для сжимаемого газа формулируется так:
полная энергия единицы массы газа величина постоянная.
Преобразуем это уравнение в температурную форму, воспользовавшись уравнением состояния газа:
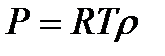 , откуда
, откуда 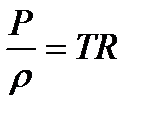 .
.
После подстановки уравнение примет вид:
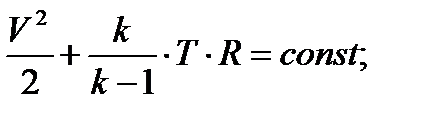
т.к. для воздуха к=1.41, R=287,14 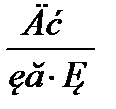 , то применительно к воздуху уравнение принимает вид :
, то применительно к воздуху уравнение принимает вид :
V 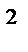 +2000T=const.
+2000T=const.
Следствие: Чем больше скорость потока, тем меньше температура в этом потоке.
Дата добавления: 2016-12-27; просмотров: 6005;











