Уравнение Бернулли для несжимаемого газа

Это уравнение было опубликовано Даниилом Бернулли в 1738г. Оно представляет собой приложение закона о сохранении энергии к элементарной струйке. Рассмотрим полную энергию секундного массового расхода газа (1.5)

,

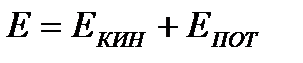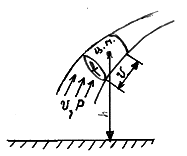
Рис. 1.5. К выводу уравнения Бернулли для несжимаемого газа

,

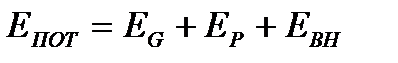где 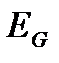— энергия положения, зависящая от высоты h;

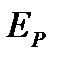— энергия давления;

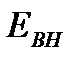— внутренняя энергия газа.

,

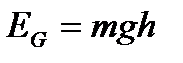Для задач аэродинамики 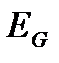=const, т. к. струйки, обтекающие самолёт в полете, находятся на одном энергетическом уровне (h=const).

Энергия давления равна произведению работы силы давления 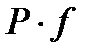, выполненной за 1 сек массой газа m (см. рис.1.5)

.

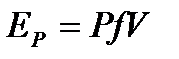Внутренняя энергия меняется при изменении температуры газа: у несжимаемого газа во всех сечениях струйки плотность 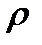=const , следовательно, и температура Т=const , т.е.

E_вн=const.

Кинетическая энергия секундного массового расход m определится по формуле:

Е_кин = ;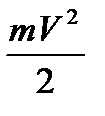

Просуммируем все виды энергии:

const + PfV + const + 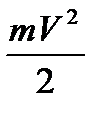= const,

PfV + 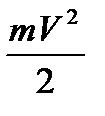= const.

Для несжимаемого газа согласно уравнению неразрывности струйки fV=const. Разделим все части уравнения на эту константу:

;

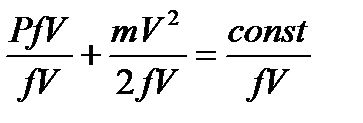т.к. 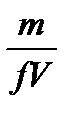= 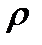, (масса газа, деленная на его объем),

то уравнение принимает вид:

P+ 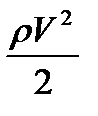= const.

где Р — статическое давление;

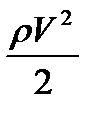— скоростной напор (динамическое давление).

Читается уравнение так:

сумма статического и динамического давления вдоль струйки — величина постоянная.

Уравнение устанавливает обратную зависимость между скоростью потока и давлением в нём.

Следствие: чем больше скорость потока, тем меньше давление в нём.

Физический смысл членов уравнения.

Р — потенциальная энергия давления единицы объёма газа.

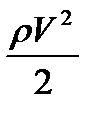— кинетическая энергия единицы объёма газа.