Входной поток требований.

С каждым отрезком времени [a,a+T], свяжем случайную величину Х, равную числу требований, поступивших в систему за время Т.

Поток требований называется стационарным, если закон распределения не зависит от начальной точки промежутка а, а зависит только от длины данного промежутка Т.

Например, поток заявок на телефонную станцию в течение суток (Т=24 часа) нельзя считать стационарным, а вот с 13 до 14 часов (Т=60 минут) – можно.

Поток называется без последействия, если предыстория потока не влияет на поступления требований в будущем, т.е. требования не зависят друг от друга.

Поток называется ординарным, если за очень короткий промежуток времени в систему может поступить не более одного требования.

Например, поток в парикмахерскую – ординарный, а в ЗАГС – нет. Но, если в качестве случайной величины Х рассматривать пары заявок, поступающих в ЗАГС, то такой поток будет ординарным (т.е. иногда неординарный поток можно свести к ординарному).

Поток называется простейшим, если он стационарный, без последействия и ординарный.

Основная теорема. Если поток – простейший, то с.в. Х_[a.a+T] распределена по закону Пуассона, т.е. .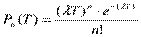

Следствие 1. Простейший поток также называется пуассоновским.

Следствие 2. M(X)=M(Х[a,a+T])=lT, т.е. за время Т в систему в среднем поступает lT заявок. Следовательно, за одну единицу времени в систему поступает в среднем l заявок. Эта величина и называется интенсивностью входного потока.

ПРИМЕР.

В ателье поступает в среднем 3 заявки в день. Считая поток простейшим, найти вероятность того, что в течение двух ближайших дней число заявок будет не менее 5.

Решение.

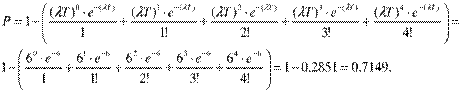По условию задачи, l=3, Т=2 дня, входной поток пуассоновский, n³5. при решении удобно ввести противоположное событие, состоящее в том, что за время Тпоступит меньше 5 заявок. Следовательно, по формуле Пуассона, получим