Асимптотические оценки переменных. Наблюдатель состояния

Определение. Асимптотической оценкой некоторой переменной 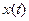называется другая физическая величина 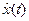такая, что выполняются условия

а) , ,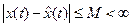

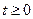б) 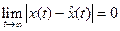. ■ (3.27)

Смысл этого определения поясняется рис. 3.5,а. Как видно, в начале работы системы значение оценки 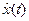значительно отличается от значения переменной 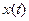. Однако с течением времени значение оценки приближается к значениям переменной и в дальнейшем их значения практически совпадают.

Обычно величину 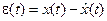называют ошибкой оценивания, а время 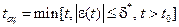– временем оценивания (рис. 3.5,а). Здесь 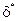– некоторая (малая)

величина.

Устройство, которое формирует асимптотические оценки переменных состояния, называется наблюдателем состояния или просто наблюдателем, а задача получения асим-

птотических оценок называется задачей оценивания.

Отметим, что оценки переменных состояния используются в системах управления для замены в управлении 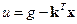тех переменных 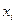, которые недоступны измерению.

Наблюдатель состояния.Если уравнения объекта имеют вид

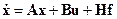, (3.28)

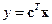, (3.29)

причём y и f– измеряемые величины, то уравнение наблюдателя полного порядка (наблюдателя Калмана) берётся в следующей форме:

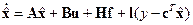, (3.30)

где l – варьируемый вектор параметров наблюдателя; – вектор состояния наблюдателя.

Схема наблюдателя состояния (3.30) при f= 0 показана на рис. 3.5,б. Из выражения (3.30) следует, что для построения наблюдателя необходимо, чтобы возмущающие воздействия, приложенные к объекту (3.28), (3.29), были доступны измерению.

При этом для решения задачи оценивания его вектора состояния x = x(t) достаточно выбрать в уравнении наблюдателя (3.30) вектор lтак, чтобы выполнялось условие

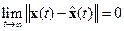. (3.31)

Найдем условия выбора вектора l, при котором выполняется условие (3.31). С этой целью определим производную по времени от ошибки оценивания 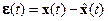. Дифференцируя по t это равенство и учитывая уравнения объекта (3.28), (3.29) и наблюдателя (3.30), получим

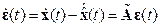, (3.32)

где

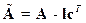. (3.33)

С учётом обозначения 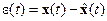условие (3.31) имеет вид