Критерий управляемости

Для оценки управляемости объектов или систем, уравнения которых представлены в форме (3.1), (3.2), используется критерий Калмана, в основе которого лежит матрица управляемости

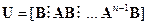. (3.3)

Здесь n = dimx – порядок объекта или системы (3.1), (3.2). В общем случае матрица U является прямоугольной с размерами 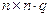, где q = dimu – размерность вектора управлений u.

Критерий управляемости. Объект (3.1), (3.2) является полностью управляемым, если

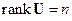, (3.4)

где n = dimx; rank–ранг матрицы. В противном случае объект является не полностью (не вполне) управляемым. ■

Если объект имеет одно управление, т. е. 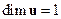, то B = b, а 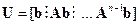– 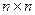-матрица. При этом условие управляемости принимает вид

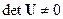. (3.5)

В соответствии с критерием управляемости Калмана матрицы выходов Си Dне влияют на свойство управляемости, поэтому часто говорят об управляемости пары А,В.

Пример 3.1.Оценить управляемость объекта

.

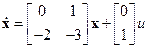Решение. Здесь n = 2, следовательно, равенство (3.3) принимает вид 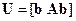. Подставляя численные значения, найдем

.

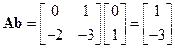Поэтому матрица управляемости

.

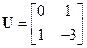В данном случае 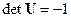, следовательно, по условию (3.5) рассматриваемый объект является полностью управляемым. ■

Уравнения объекта в рассмотренном примере имеют каноническую управляемую форму (КУФ). В связи с этим отметим, что если уравнения объекта (системы) записаны в КУФ, то объект (система) являются вполне управляемыми, т. е. проверять их управляемость в этом случае не нужно.

Пример 3.2.Объект описывается уравнением

.

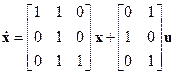Оценить его управляемость.

Решение. Здесь n = 3, поэтому из равенства (3.3) находим 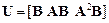. В нашем случае

, .

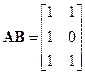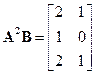Следовательно, матрица управляемости

.

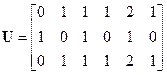Ранг этой матрицы Uравен двум, поэтому, в соответствии с критерием управляемости, этот объект не вполне управляемый, так как n = 3. ■

Доказательство критерия управляемости.Для доказательства критерия управляемости (3.4) найдём условия, при которых можно определить управление u, переводящее объект из произвольного состояния x₀ ¹ 0 при t = 0 в состояние x(t₁) = 0 при t = t₁. Вектор состояния x(t) объекта (3.1), (3.2), как известно, определяется формулой Коши:

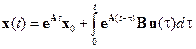. (3.6)

Предположим, u(t) – это управление, которое переводит систему (3.1), (3.2) из состояниях₀ в состояние x(t₁) = 0 при 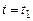. Тогда при 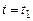из (3.6) получим

.

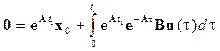Умножая это выражение на exp(–At₁) слева, получим

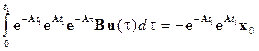
или

.

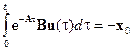Как известно, матрица exp(–At) может быть представлена в виде суммы

,

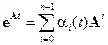где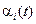 – некоторые функции времени. Заменим здесь t на 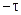и подставим в предыдущее равенство. В результате получим

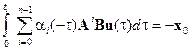
или, раскрывая сумму,

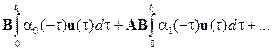
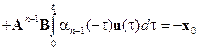(3.7)

Обозначим

,

,

.

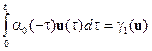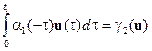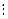
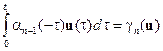Тогда равенство (3.7) можно записать следующим образом:

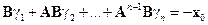. (3.8)

Если ввести вектор-столбец 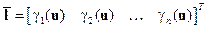, то равенство (3.8) с учетом обозначения (3.3) примет вид

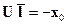. (3.9)

Рассмотрим два случая. Пусть управление u скалярное, т.е. B = b, тогда в системе (3.9) 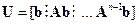– квадратная 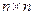-матрица. Чтобы в этом случае найти искомое управление u, которое переводит состояние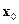в состояние x(t₁) = 0 при 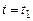, прежде всего, необходимо разрешить систему линейных алгебраических уравнений (3.9) относительно вектора 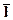. Как известно, эта система имеет решение только тогда, когда определитель ее матрицы равен n, что соответствует условию (3.5) критерия управляемости.

Если управление u векторное, то матрица системы (3.9) является прямоугольной, причем число её столбцов больше числа её строк. В этом случае система (3.9) будет иметь решение, если среди столбцов матрицы U найдется n линейно независимых, из которых можно составить квадратную 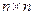матрицу, определитель которой не будет равен нулю. Это требование, очевидно, эквивалентно условию (3.4) критерия управляемости. ■

Таким образом, если уравнения динамической системы или объекта управления представлены в виде (3.1), (3.2), то их управляемость можно проверить с помощью критерия Калмана. Отметим, что уравнения системы в указанном виде должны быть найдены с учетом требования её полного и однозначного описания, вытекающего из законов природы, описывающих процессы в исследуемой системе.

Если же уравнения (3.1), (3.2) получены, например, из уравнений «вход-выход» или из передаточных функций, найденных путем эквивалентных преобразований структурной схемы системы, без соблюдения соответствующих условий (см. пример 2.9), то применение критерия управляемости не имеет смысла, так как эти уравнения могут не содержать информации о свойстве управляемости исследуемой системы.

Свойство управляемости, как будет показано ниже, играет определяющую роль при построении модального и оптимального управлений.