Определение и критерий наблюдаемости

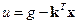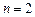На рис. 1.10 приведена схема системы с управлением по состоянию, а на рис. 3.3 схема формирования комбинированного управления при . Здесь Д₁,Д₂– датчики, измеряющие переменные состояния x₁ и x₂; K₁и K₂ – усилители, с помощью которых осуществляется умножение x₁ на K₁ и x₂ на K₂.

Как видно, для построения управления по состоянию необходимо, чтобы все переменные состояния объекта управления (см. рис. 1.10) были доступны измерению. Однако очень часто это невозможно. Обычно измеряются некоторые другие величины, например, управляемая переменная, отклонение и т.д. Причем число измеряемых величин, как правило, меньше числа переменных состояния.

Возникает задача: по измеряемым переменным определить значения неизмеряемых переменных состояния. Это и есть задача наблюдения. Объекты управления или системы, которые допускают решение этой задачи, называются наблюдаемыми. Объекты или системы, которые не допускают решения этой задачи, называются не вполне(не полностью) наблюдаемыми.

Математически задача наблюдаемости формулируется следующим образом. Пусть уравнения объекта (или системы) имеют вид

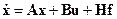, (3.11)

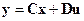, (3.12)

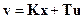. (3.13)

Здесь v– вектор измеряемых (наблюдаемых) переменных; y– вектор управляемых величин; u и f– векторы управлений и возмущений.

Среди измеряемых переменных 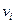могут быть: переменные состояния 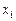, регулируемые величины 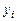, отклонения 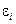, возмущающие воздействия 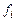и другие переменные. Мы в дальнейшем будем полагать, что вектор 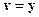. Кроме того, будем предполагать, что матрицы A,B,C, D,H известны.

Определение. Объект (или система) (3.11) – (3.13) называется наблюдаемым(наблюдаемой), если по результатам измерения векторов 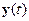, 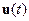и 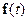на интервале 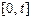можно определить значение вектора при .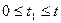

В противном случае объект (или система) называется не вполне наблюдаемым(не вполненаблюдаемой). ■

Для исследования свойства наблюдаемости объектов управления (или систем) применяют критерий наблюдаемости.

В соответствии с формулой Коши для определения 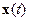системы (3.11) – (3.13) при 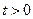достаточно найти значение 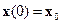, так как

.

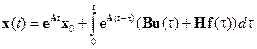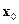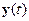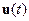Следовательно, для исследования свойства наблюдаемости достаточно оценить возможность определения по , и 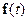.В соответствии с критерием наблюдаемости Калмана для этой цели используется матрица наблюдаемости, которая имеет следующий вид:

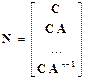, (3.14)

где, как и ранее, .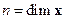

Критерий наблюдаемости. Объект (или система) (3.11), (3.12) является наблюдаемым (наблюдаемой), если

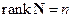, (3.15)

где 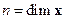. В противном случае объект (или система) является не вполне (не полностью) наблюдаемым (наблюдаемой). ■

Если 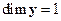, т. е. 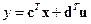, то

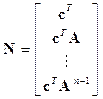(3.16)

квадратная матрица. В этом частном случае условие наблюдаемости имеет вид

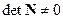. (3.17)

Как видно, матрицы B и H из (3.11) не влияют на свойство наблюдаемости.

Пример 3.3.Предположим, объект описывается уравнениями

, .

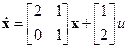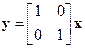Оценить его наблюдаемость.

Решение. Так как 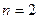, то согласно (3.14), матрица

.

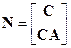Вычислим сначала матрицу

,

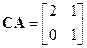и составим по (3.14) матрицу наблюдаемости

.

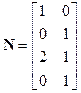Очевидно, 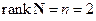. Следовательно, данный объект является вполне наблюдаемым. ■

Пример 3.4.Оценить наблюдаемость объекта, который описывается уравнениями

, .

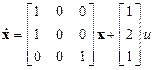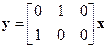Решение. Здесь 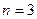. Поэтому, согласно (3.14), матрица наблюдаемости

.

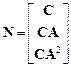Вычисляем последовательно

, .

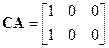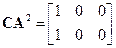Следовательно, матрица наблюдаемости

.

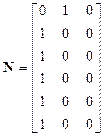Полученная матрица имеет 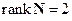, т.е. данный объект не полностью наблюдаемый, так как . ■

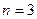Замечание.Если уравнения объекта или системы записаны в канонической наблюдаемой форме (КНФ), то они являются вполне наблюдаемыми, т.е. проверять наблюдае-

мость в этом случае не нужно.

Доказательство критерия наблюдаемости. Имея в виду уравнения объекта (3.11) и (3.12) при 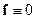, найдём последовательно производные по времени вектора y (как вектора измеряемых переменных). Дифференцируя (3.12) по t и учитывая (3.11), будем иметь

,

,

.

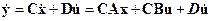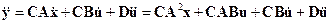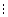
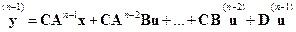Здесь используется общепринятое обозначение: 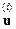– i-я производная переменной u по времени t.

Образуем векторы-столбцы из векторов y, u и их производных по времени до 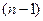-й включительно:

, .

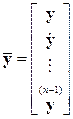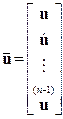С помощью этих обозначений предыдущие равенства можно записать в виде единой системы уравнений

,

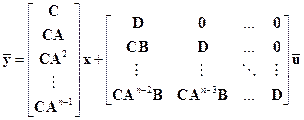которую с учетом обозначения матрицы наблюдаемости (3.14) можно представить в виде

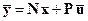, (3.18)

где матрица P очевидным образом определяется из предыдущего равенства.

Если измеряется скалярная величина, т.е. С является вектором c^T, то матрица наблюдаемости N – квадратная. В этом случае при известных переменной 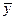и векторе 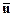вектор состояния x можно найти из уравнения (3.18), если только 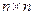-матрица N имеет обратную. Известно, однако, что матрица имеет обратную матрицу, если только её определитель не равен нулю. Отсюда следует, что в скалярном случае вектор состояния x можно найти из уравнения (3.18), если только 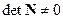. Это условие, очевидно, соответствует условию (3.17), причём, если оно выполняется, то

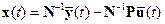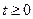, . (3.19)

В общем случае, если 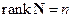, то в уравнении (3.18) всегда можно выбрать n линейно независимых строк матрицы Nи записать для них уравнение, аналогичное уравнению (3.19), которое определяет вектор 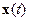при любом . ■

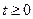Таким образом, условия критерия наблюдаемости являются необходимыми и достаточными для определения вектора состояния по результатам измерения доступных переменных. Практически, критерий наблюдаемости, как будет показано ниже, определяет условия, при которых можно найти значения не самих переменных состояния, а значения их оценок.