Полнота объектов и систем управления

Это свойство характеризует связь входных и выходных величин объектов или систем с их переменными состояния в интегральном смысле. По этому свойству объекты или системы могут быть либо полными, либо неполными.

Определение. Объект называется полным, если он является полностью управляемым и полностью наблюдаемым, в противном случае объект является неполным.

Согласно рис. 3.4,б, у полного объекта 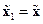, т.е. составляющие 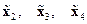вектора 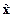отсутствуют. В то же время, если объект неполный, то в его представлении, аналогичном приведённому на рис. 3.4,б, имеется, по крайней мере, один ненулевой вектор 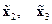или .

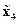Аналогично определяется полнота систем управления по отношению к входным воздействиям (чаще всего задающим) и выходным измеряемым переменным.

В зависимости от формы уравнений заданной модели объекта или системы можно использовать различные критерии полноты.

Если объект или система заданы уравнениями в переменных состояния типа (3.11), (3.12), то в качестве критерия полноты, в соответствии с определением, можно использовать критерии управляемости и наблюдаемости, т.е. для оценки полноты достаточно найти матрицыU (3.3), N (3.14) и ранги этих матриц.

Критерий полноты 1.Если уравнения объекта или системы имеют вид (3.11), (3.12), и если 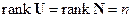, где 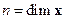, то объект или система являются полными. В противном случае – неполными. ■

Если же уравнения объекта или системы заданы в форме вход-выход

,

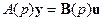где 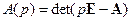, , 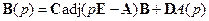то здесь могут встретиться два случая.

Если 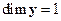и , то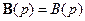 –полином. Тогда аналитическое условие полноты имеет вид

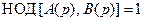.(3.21)

Критерий полноты 2. Одномерный объект или система являются полными, если полиномы 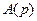и 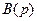в их уравнениях «вход-выход»не имеют общих множителей или, что то же самое, общих корней. В противном случае объект или система являются неполными. ■

В равенстве (3.21) НОД – наибольший общий делитель.

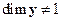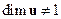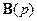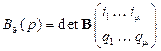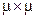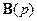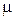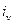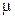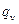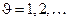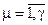Если же или (и) , то будет матрицей. Поэтому для проверки полноты сначала необходимо найти полиномы , как всевозможные миноры размером , составленные из элементов матрицы , стоящих на пересечении любых её строк и столбцов . Причем , а , где

.

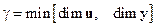Затем находится полином

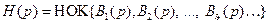, (3.22)

где НОК – наименьшее общее кратное.

Критерий полноты 3. Многомерный объект или система являются полными, если 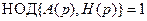, иначе – неполными.

Из приведенных формулировок критериев полноты следует, что если объект или система являются многомерными, то исследование их полноты удобнее проводить, пользуясь критерием полноты 1. Если же объект или система одномерные, то удобнее пользоваться критерием полноты 1 или критерием полноты 2.

При этом очень важно иметь в виду, что фигурирующий в выражении (3.21) и других равенствах полином 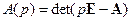, где A – матрица из уравнений в переменных состояния данного объекта или системы, полученных с учетом полноты их описания.

Пример 3.5.Оценить полноту объекта, если его уравнение «вход-выход» имеет вид

,

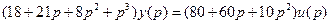причем полином

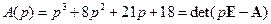. (3.23)

Решение. Так как задано уравнение «вход-выход», то воспользуемся критерием полноты 2. С этой целью найдем сначала корни полинома 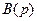, для чего решим уравнение

.

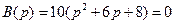Отсюда 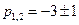, т. е. 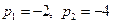. Следовательно,

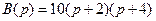.(3.24)

Так как степень полинома 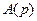равна трем, то его можно представить в виде

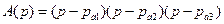.(3.25)

Полагая в (3.23) 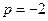, получим 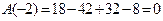. Следовательно, число 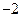является одним из корней полинома 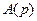и, согласно (3.25), можно записать .

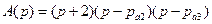Таким образом, в рассматриваемом случае полиномы 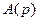и 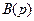имеют общий множитель 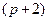. Поэтому в соответствии с критерием 2 исследуемый объект является неполным. ■

Представим передаточную функцию рассматриваемого объекта с учетом равенств (3.24) и (3.25) следующим образом:

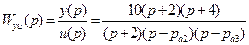
или

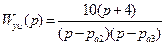. (3.26)

Множитель 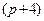здесь не сокращается, так как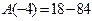 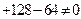,т.е. число – 4 не является нулем полинома .

Таким образом, передаточная функция (3.26) рассматриваемого объекта описывает лишь его полную часть, и после сокращения общих множителей в числителе и в знаменателе она не содержит информации о его неполной части. Фактически, сокращающийся в этих случаях множитель является характеристическим полиномом неполной части системы.

В некоторых случаях неполноту объекта или системы можно установить непосредственно по структурной схеме. Например, объект является неполным, если он включает:

- параллельное соединение звеньев, знаменатели передаточных функций которых имеют одинаковые полюсы;

- последовательное соединение таких звеньев, что у одного звена имеются полюсы или нули, равные нулям или полюсам другого звена.

В этих случаях образуются сокращающиеся нули и полюсы и, как следствие, возникает неполнота объекта или системы. В частности, к первому из указанных случаев относится система ( см. рис. 2.36), рассмотренная в примере 2.9. Второй случай всегда имеет место при синтезе САУ, например, методом желаемых частотных характеристик, когда допускается компенсация нулей объекта полюсами корректирующего звена и (или) наоборот.

Однако указанные здесь случаи не охватывают всех возможных случаев неполноты динамических систем, поэтому в сомнительных случаях необходимо применять какой-либо из указанных выше критериев полноты.

Таким образом, мы снова приходим указанному в § 2.7 выводу: при преобразовании моделей «вход-выход» динамических систем информация о неполных частях систем может быть потеряна из-за сокращения общих множителей. Поэтому целесообразно иметь в виду следующее.

Замечание. Характеристический полином системы можно определять как знаменатель передаточной функции только тогда, когда есть уверенность, что рассматриваемая система является полной. В противном случае характеристический полином указанным способом может быть определён неверно. ■

К ошибкам аналогичного типа могут приводить практически все методы преобразования моделей систем в форме передаточных или переходных функций, а также частотных характеристик. Очень часто этих ошибок можно избежать, если в процессе преобразований моделей «вход-выход» соблюдать правило порядков.

Правило порядков. Порядок системы равен сумме порядков всех её элементов и связей между ними. ■

Следовательно, при корректном преобразовании модели системы всегда выполняется условие: порядок модели после преобразования равен порядку модели до преобразования.

В качестве иллюстрации к приведенным утверждениям укажем, что если характеристический полином системы, схема которой приведена на рис. 2.36, определять по её передаточной функции (2.39), как полином знаменателя, или по уравнению вход-выход (2.40), то получаемый результат не будет соответствовать действительности. То же самое относится и к задаче определения порядка этой системы по её передаточной функции (2.39) или по уравнению вход-выход (2.40).

Этот же вывод относится и к случаю определения по передаточной функции (3.26) порядка или характеристического полинома системы, которая рассматривается в примере 3.5.