Определение моделей систем управления

В соответствии с изложенным выше, для получения характеристик и исследования свойств САУ необходимо иметь её математическую модель, т.е. передаточные функции, уравнения вход-выход или уравнения в переменных состояния.

Рассмотрим порядок определения моделей систем. Обычно, исходя из описания САУ, можно составить её функциональную, а затем и структурную схему. Уравнения или передаточные функции элементов структурной схемы или определяются, исходя из принципов их работы, или записываются, исходя из типа звена: пропорциональное, инерционное и т.п.

По структурной схеме системы может быть найдена та или иная модель системы либо методом последовательных преобразований, либо по формуле Мэйсона [3], либо методом преобразований уравнений в переменных состояния звеньев системы. Покажем это на примере.

Пример 2.9. Предположим, система имеет структурную схему, приведённую на рис. 2.36, а передаточные функции её звеньев определяются выражениями:

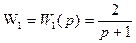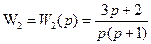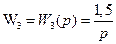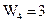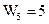, , , , (2.38)

Найти передаточную функцию, и записать уравнение «вход-выход» системы.

Решение. В данном случае схема проста, поэтому воспользуемся методом последовательных преобразований.

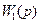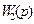Звенья с передаточными функциями и соединены параллельно, поэтому

.

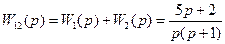Звенья с передаточными функциям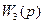и и 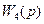образуют соединение с отрицательной обратной связью, поэтому

.

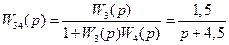Звенья с передаточными функциям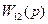и и 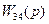соединены последовательно, поэтому

.

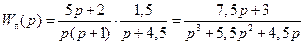Полученная функция является передаточной функцией прямой связи системы. Поэтому обозначена .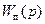

Звено с передаточной функцией 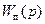охвачено отрицательной обратной связью с передаточной функцией 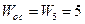, поэтому передаточная функция 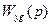системы, показанной на рис. 2.36, будет равна

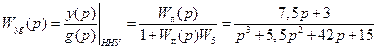. (2.39)

Аналогичный результат можно получить с помощью формулы Мэйсона.

Для вывода операторного уравнения «вход-выход» системы второй и четвёртый члены этого равенства рассматриваются как пропорция. Раскрывая её, получим уравнение «вход-выход» системы

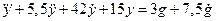. (2.40)

Однако полученные модели (2.39) и (2.40) рассматриваемой системы являются некорректными. Действительно, в соответствии с ними порядок системы равен трём. В то же время, по правилу порядков (с. 78) рассматриваемая система имеет четвёртый порядок, поскольку первое и третье звенья имеют первый порядок, второе звено – второй, а третье и четвёртое звенья – нулевой порядок, т.е. сумма порядков звеньев системы равна 4.

Как будет показано ниже, полученное противоречие означает, что система, схема которой приведена на рис. 2.36, является неполной. Поэтому её корректную модель можно получить лишь на основе уравнений в переменных состояния.

С этой целью на структурной схеме (рис. 2.36) обозначим входы g_i и выходы y_i динамических звеньев i = 1, 2 и 3. Входы и выходы четвертого и пятого звеньев не обозначаем, так как эти звенья являются безынерционными.

Применяя к передаточным функциям звеньев (2.38) формулы перехода от передаточных функций к уравнениям в переменных состояния, например, соответствующие канонической управляемой форме, получим:

1-е звено: , ;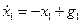

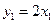2-е звено: , ;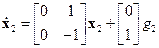

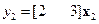3-е звено: , .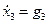

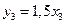В соответствии со структурной схемой системы (рис. 2.36) запишем уравнения связей между её звеньями:

g₁ = g₂ = g – 5y₃; y₁₂ = y₁ + y₂; g₃ = y₁₂ – 3y₃; y = y₃. (2.41)

Здесь через y₁₂ обозначен выход сумматора, который суммирует переменные y₁ и y₂.

Далее из уравнений связи и уравнений в переменных состояния исключаем все промежуточные переменные g_i,, y_i и y₁₂:

g₁ = g₂ = g – 7,5 x₃; y₁₂ = 2 x₁ + [2 3] x₂;

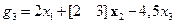; y = 1,5x₃;

; ,

.

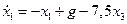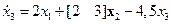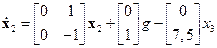Наконец, объединяя переменные состояния x₁, x₂₁, x₂₂ и x₃ в один вектор 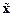, получим уравнения состояния и выхода рассматриваемой системы в векторно-матричной форме:

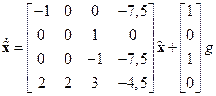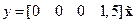, . (2.42)

Как видно, полученные уравнения по форме совпадают с общей формой моделей линейных систем (2.9), (2.10) (при 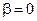) и, действительно, соответствуют системе четвёртого порядка.

Для сравнения с результатами, полученными выше, найдём характеристический полином А(р) и передаточную функцию W_yg(p) системы по известным формулам:

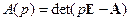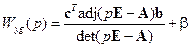, . (2.43)

Здесь 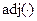– присоединённая матрица. В случае уравнений (2.42) имеем

,

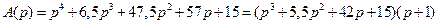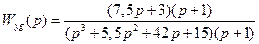. (2.44)

В среде MATLAB искомую передаточную функцию можно получить, введя следующие команды:

% создаём lti-модели каждого звена:

W1 = tf(2, [1 1]); W2 = tf([3 2],[1 1 0]);

W3 = tf(1.5, [1 0]); W4 = tf(3, 1); W5 = tf(5, 1);

Wyg = feedback((W1+W2)*feedback(W3, W4), W5)

Wyg.Variable = 'p'

- результат (transfer function W_yg(p)):

7.5p^2 + 10.5p + 3

-------------------------------- (2.45)

p^4 + 6.5p^3 + 47.5p^2 + 57p + 15

Эта функция, очевидно, эквивалентна функции (2.44) и отличается от полученной выше передаточной функции (2.39) множителем (р + 1) и в числителе, и в знаменателе. Как будет показано ниже, наличие такого множителя свидетельствует, что рассматриваемая система является неполной.

Отметим, что корректность передаточной функции (2.45) обусловлена тем, что lti-модели MATLAB фактически представляют собою модели в переменных состояния (вход-состояние-выход).

Г л а в а 3