Нули и полюсы передаточных функций

Так как передаточная функция динамического объекта или системы обычно является отношением двух полиномов, то её всегда можно представить следующим образом:

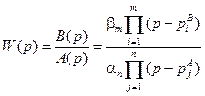, (2.26)

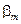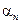где и – коэффициенты пр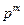и и 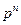соответственно полиномов 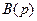и , , , , , .

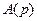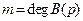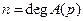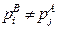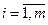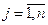Комплексные (в общем случае) числа 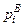называются нулями передаточной функции, т. е. корни уравнения 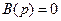– это нули W(p) (2.26). Числа 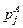называются полюсами передаточной функции, т.е. корни уравнения 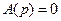–это полюсы W(p) (2.26).

Полюсы и нули передаточной функции (2.26) могут быть как вещественными, так и комплексными. Поэтому передаточную функцию произвольного вида всегда можно представить множителями с вещественными коэффициентами следующим образом:

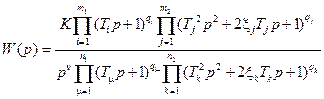. (2.27)

Здесь K – коэффициент передачи (коэффициент усиления, если К >1) рассматриваемого объекта или системы; 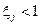, 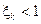– коэффициенты демпфирования; Т_i, T_j, T_m, T_k – постоянные времени; 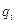, , 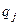, 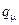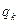– постоянные числа.

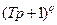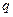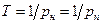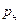Множители вида соответствуют вещественным нулям или полюсам кратности , причем , где и 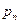– вещественные нули или полюсы.

Множители вида 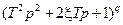, где 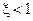, соответствуют паре комплексных нулей или полюсов кратности q, а множитель 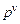соответствует тем нулям и полюсам данной передаточной функции, которые равны нулю, причем .

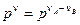Представление передаточной функции в виде (2.27) применяется при исследовании различных свойств линейных динамических систем. В частности, оно позволяет достаточно быстро построить вручную логарифмические асимптотические частотные характеристики системы по заданной передаточной функции вида (2.26).

Переходя к изложению соответствующего алгоритма, рассмотрим сначала некоторые свойства логарифмических асимптотических характеристик. Например, множителям вида 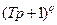, находящимся в числителе (2.27), соответствуют логарифмические амплитудная и фазовая характеристики, показанные на рис. 2.26. Как видно, в интервале частот 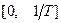наклон асимптотической ЛАЧХ равен нулю, а в интервале частот 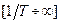он равен 20q дБ/дек. Фазовая характеристика положительна и изменяется от нуля до πq/2.

Если же этот множитель находится в знаменателе W(p) (2.27), то соответствующая ему логарифмическая амплитудно-частотная характеристика имеет тот же вид, но наклон в интервале частот 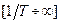равен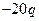дБ/дек, а фазовая характеристика находится в интервале .

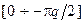Множителям вида 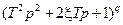, находящимся в числителе передаточной функции (2.27), соответствуют асимптотические характеристики, показанные на рис. 2.27.

Их вид аналогичен предыдущему случаю (рис. 2.26), но в интервале частот 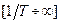наклон амплитудной характеристики равен 40q дБ/дек, а фазовая характеристика изменяется от нуля до πq.

Если же этот множитель находится в знаменателе W(p) (2.27), то соответствующая ему логарифмическая амплитудная характеристика имеет вид, аналогичный предыдущему случаю, но в интервале частот 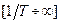наклон амплитудной характеристики равен –40q дБ/дек, а фазовая характеристика изменяется от нуля до –p q.

Однако в случае множителя второго порядка необходимо иметь в виду следующее. Если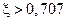, то можно ограничиться построением лишь асимптотических характеристик. Если же 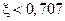, то, как отмечалось выше, к асимптотической амплитудной характеристике в обязательном порядке необходимо добавлять поправки, увеличенные в q раз и взятые из специальных номограмм.

Аналогично множителю 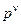в знаменателе (2.27) соответствуют логарифмические амплитудные характеристики, показанные на рис. 2.28. Они также имеют наклон 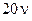дБ/декили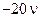дБ/дек в зависимости от знака числа ν, но во всем интервале частот от 0 до ∞. При этом на частоте ω = 1 эти характеристики всегда проходят через точку 20lgK.

Фазочастотные характеристики, соответствующие множителю 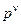в знаменателе (2.27), равны 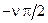и являются постоянными во всем интервале частот от 0 до ∞.

Из изложенных свойств нулей и полюсов передаточных функций (2.26) вытекает следующий алгоритм построения соответствующих логарифмических асимптотических частотных характеристик (ЛАЧХ) вручную:

- представить заданную передаточную функцию в виде (2.27);

- найти 20 log K;

- найти частоты сопряжения , ;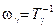

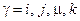- перенумеровать частоты 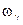и коэффициенты 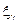в порядке

возрастания численных значений 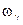, т.е. ;

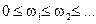- построить ось абсцисс в логарифмическом масштабе; из точки 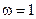восстановить перпендикуляр и отложить на нём 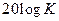(это значение может быть и отрицательным). Через полученную точку провести характеристику, соответствующую множителю ;

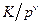- искомая ЛАЧХ будет совпадать с линией, полученной в предыдущем пункте, от начала оси абсцисс, вплоть до частоты 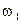. В точке 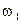наклон ЛАЧХ изменится на 20 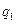дБ/дек, если 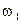соответствует множителю 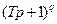в числителе, и на –20 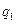дБ/дек, если 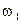соответствует этому же звену, но оно находится в знаменателе (2.27). Если же частота 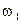соответствует множителю второго порядка, то наклон изменится на 40 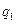дБ/дек, если этот множитель в числителе, и на – 40 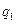дБ/дек, если он находится в знаменателе. Полученная характеристика продолжается до частоты 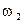, на которой наклон изменяется аналогично. Далее описанный процесс продолжается до последней частоты сопряжения 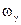в (2.27).

При необходимости в точках излома линейных участков могут быть внесены указанные выше поправки. Для построения фазовой характеристики строятся характеристики всех множителей (2.27), после чего производится их суммирование вдоль оси ординат.

Пример 2.7. Динамическое звено описывается передаточной функцией

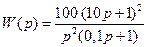. (2.28)

Построить логарифмические асимптотические частотные характеристики.

Решение. Находим 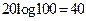дБ. В данном случае n = 2, частота 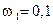; частота , , , , .

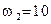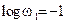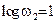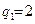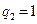Асимптотическая логарифмическая АЧХ, построенная по этим данным с помощью изложенного выше алгоритма, приведена на рис. 2.29.

Построение фазовой характеристики. Множителю p² в знаменателе передаточной функции (2.28) соответствует фазовая характеристика 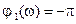(рис. 2.30). Множителю 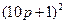, находящемуся в числителе W(p),соответствует фазовая характеристика 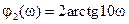, также показанная на рис. 2.30. Наконец множителю 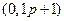, находящемуся в знаменателе, соответствует фазовая характеристика .

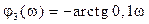Суммируя эти три характеристики вдоль оси ординат, получим фазочастотную характеристику 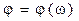заданного звена, показанную на рис. 2.30 жирной линией.

Итак, графики на рис. 2.29 и на рис. 2.30 представляют искомые частотные амплитудную и фазовую характеристики системы с передаточной функцией (2.28). ■

Отметим еще раз, что в настоящее время временные и частотные характеристики, в том числе и логарифмические, целесообразнее строить с помощью ЭЦВМ или ПЭВМ, используя специальные подпрограммы, пакеты и т.д. Покажем это на примере.

Пример 2.8. Построить годограф АФЧХ и ЛЧХ системы с передаточной функцией (2.28) с помощью ПЭВМ, используя программный пакет MATLAB.

Решение. Предварительно представим функцию (2.28) в виде отношения двух полиномов, а затем введём в командном окне MATLAB следующие команды:

sys = tf([10000 2000 100], [0.1 1 0 0]);

nyquist(sys)

В результате на экране монитора появится годограф АФЧХ заданной системы.

Для построения в среде MATLAB логарифмических частотных характеристик, после приведенной выше команды sys = tf(•) или после команды nyquist(sys) вводим команду:

bode (sys)

После этого на экране монитора появятся графики амплитудной и фазовой логарифмических характеристик этой же системы, близкие к приведенным на рис. 2.29 и на рис. 2.30. ■

Подчеркнём также, что изложенные выше свойства временных и частотных характеристик необходимы для проверки правильности полученных с помощью ЭВМ данных.

Особые звенья САУ

Наряду с обычными, рассмотренными ранее динамическими звеньями, которые описываются обыкновенными дифференциальными уравнениями, в САУ встречаются звенья другого типа, которые описываются более сложными уравнениями. Это либо уравнения с запаздыванием, либо уравнения в частных производных, либо уравнения с иррациональными или трансцендентными выражениями. Такие звенья называются особыми. К особым звеньям иногда относят и обычные звенья с особенностями (неустойчивые, неминимально-фазовые).

Звено чистого запаздывания.К звеньям с запаздыванием относятся звенья, реакция которых появляется с некоторой задержкой по отношению к моменту возникновения входного воздействия.

В качестве простейшего примера объекта с запаздыванием рассмотрим транспортёр (рис. 2.31,а), используемый для перемещения сыпучих материалов на некоторое расстояние l.

Входным воздействием 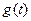транспортёра является количество вещества, высыпающегося из бункера на транспортёр в единицу времени; выходной переменной 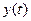является также количество вещества, но ссыпающегося с транспортёра в единицу времени.

Если при пустом работающем транспортёре заслонку бункера открыть в момент времени 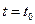, то вещество на выходе транспортера появится, очевидно, лишь по истечении времени 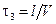, где V – скорость движения ленты транспортера, а l – длина транспортера.

Величина 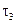называется временем запаздывания или просто запаздыванием.

В тех случаях, когда запаздывание обусловлено транспортировкой вещества на некоторое расстояние, его ещё называют транспортным запаздыванием или чистым запаздыванием. Уравнение звена с чистым запаздыванием имеет вид

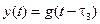
или в изображениях по Лапласу

.

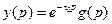Отсюда следует передаточная функция звена чистого запаздывания

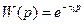. (2.29)

Порядок звена с чистым запаздыванием (2.29) равен бесконечности, поэтому его уравнение в переменных состояния обычно не записывают. Запаздывание же включают в аргумент входного воздействия или выходной переменной инерционных звеньев, соединенных со звеном чистого запаздывания.

Например, обычное инерционное звено, как известно, описывается уравнениями

, .

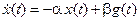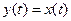Поэтому, если это звено в системе расположено перед или после звена с чистым запаздыванием, то уравнения этого соединения будут иметь вид

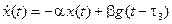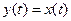, . (2.30)

Такое соединение называется инерционным звеном с запаздыванием. Его передаточная функция

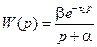. (2.31)

Отметим, что порядок инерционного звена с запаздыванием, как и звена (2.29), равен бесконечности. Проявляется это, в частности, в том, что для определения выходной переменной звена (2.30), (2.31) необходимо задать значения этой переменной в бесконечном множестве точек – на интервале времени .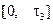

Запаздыванием обладают также трубопроводы, длинные линии электросвязи, протяженные объекты других типов.

Иррациональные звенья.Объекты или системы, распределённые в пространстве (такие как: нагревательные печи, ректификационные колонны, большие химические реакторы и т.д.), описываются уравнениями в частных производных. Однако анализ таких уравнений достаточно сложен, поэтому с приемлемой для практики точностью их стремятся заменить обыкновенными дифференциальными уравнениями. В результате применения преобразования Фурье к последним и последующей замены 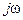на p получаются передаточные функции указанных объектов, но с иррациональными выражениями. Обычно эти функции имеют вид

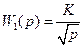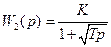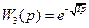, , . (2.32)

Динамические звенья с передаточными функциями данного типа называются иррациональными звеньями. Отличительная особенность этих передаточных функций в том, что они не являются полиномами от р. Поэтому анализ систем с иррациональными звеньями требует применения специальных методов. Чаще всего для этих целей применяются частотные методы и рассмотренные выше частотные характеристики.

Неустойчивые звенья.Рассмотрим звено, описываемое дифференциальным уравнением

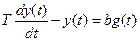. (2.33)

Корень соответствующего ему характеристического уравнения 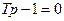равен 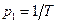, т.е. больше нуля. Поэтому свободная составляющая решения уравнения (2.33) описывается возрастающей экспонентой

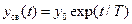. (2.34)

График ее изменения показан на рис. 2.32. Как видно, свободная составляющая выходной переменной y_св данного звена монотонно возрастает с ростом t, пока не достигнет насыщения. Из-за возрастания переменных такие звенья называются неустойчивыми.

Причиной возрастания 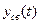(2.34) являются, в общем случае, корни характеристического уравнения, имеющие положительную вещественную часть (говорят, «правые» корни). Именно этот факт является основной особенностью неустойчивых звеньев.

Определение. Если хотя бы один из корней характеристического уравнения динамического звена имеет положительную вещественную часть, то такое звено называется неустойчивым.■

Примером неустойчивого звена может служить асинхронный двигатель. Его механическая характеристика (зависимость вращающего момента М от угловой скорости ω) приведена на рис. 2.33.

При угловой скорости близкой к ω₂ и M = M_c2 характеристика M(ω) имеет положительную производную по скорости ω, что свидетельствует о неустойчивости данного режима работы асинхронного двигателя. При малейшем отклонении скорости вращения от величины ω₂ двигатель либо останавливается, либо его скорость начинает увеличиваться, а затем уменьшаться, пока не достигнет устойчивого значения, соответствующего какой-либо точке на верхней части графика M(ω).

Неминимально-фазовые звенья.Как отмечалось выше, если динамическое звено имеет передаточную функцию

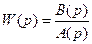, (2.35)

где 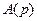, 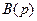– некоторые полиномы с вещественными коэффициентами, то корни уравнения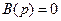, т.е. числа 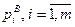называются нулями передаточной функции (2.35). Отметим, что корни уравнения 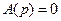, т.е. числа 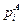, , 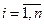называются полюсами этой функции.

Определение. Если вещественные части всех нулей передаточной функции некоторого динамического звена (2.35) являются отрицательными, т.е.

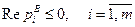, (2.36)

то соответствующее звено называется минимально-фазовым. Если же существует хотя бы один нуль с положительной вещественной частью (правый), т.е.

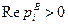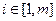, , (2.37)

то соответствующее звено называется неминимально-фазовым. ■

Наличие правых нулей (с положительной вещественной частью) и является основной особенностью неминимально-фазовых звеньев. Отметим здесь, что корни или нули с отрицательными вещественными частями часто называются «левыми».

Если в передаточной функции 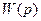заменить p на 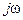, то как известно, выражение 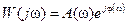является комплексным коэффициентом передачи соответствующего звена. Предположим звено с 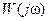– минимально-фазовое, и его фазовая характеристика 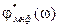имеет вид, показанный на рис. 2.34.

Если некоторая передаточная функция 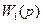отличается от 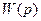только знаком вещественной части одного из нулей, то соответствующая фазовая характеристика 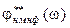будет аналогична по форме 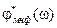, но больше её по величине, как показано на рис. 2.34. Именно поэтому звенья с 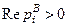и называют неминимально-фазовыми.

Переходные функции h₁ – минимально-фазового и h₂ – неминимально-фазового звеньев показаны на рис. 2.35,а.На этом рисунке 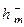– это отрицательное перерегулирование. Отрицательное перерегулирование является ещё одной особенностью неминимально-фазовых звеньев.

Примером неминимально-фазового звена является паровой котёл. При увеличении отбора пара из него уровень воды в нём, вообще говоря, должен понижаться. На самом деле он сначала повышается, а затем уже понижается.

К неминимально-фазовым звеньям может относиться и мостовая RC-цепочка, показанная на рис. 2.35,б. Её передаточная функция имеет следующий вид:

,

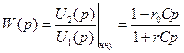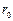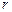причём величины и определяются выражениями

, .

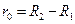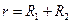Как видно, при 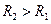мостовая RC-цепочка (рис. 2.35,б) является неминимально-фазовым звеном.

Подчеркнем, что если объект является неминимально-фазовым, то построить для него минимально-фазовую, устойчивую систему управления можно только в том случае, когда число управляющих воздействий у объекта больше числа управляемых переменных. Причем это условие является лишь необходимым условием возможности решения указанной задачи синтеза. Другими словами, скомпенсировать неминимально-фазовость объекта в системе управления можно лишь с помощью дополнительных (сверх числа управляемых переменных) управлений.