Энергия упругих колебаний

При распространении плоской продольной волны элемент массы среды Δm₀ = ρ₀ΔV совершает движение вдоль направления распространения волны. При этом его кинематическая энергия

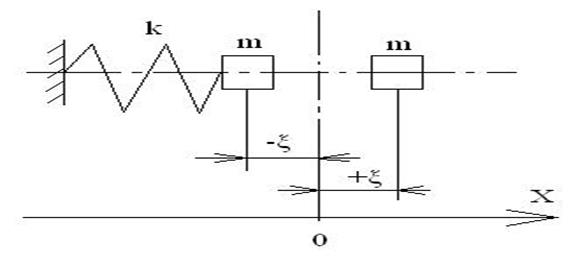
Рисунок 2.4 - К выводу энергии упругих колебаний.

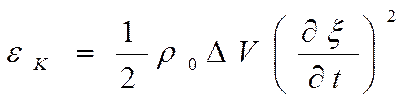, (2.12)

где ξ – смещение от положения равновесия.

На единичный объем приходится кинетическая энергия

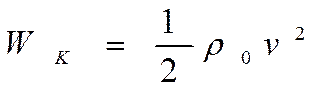(2.13)

Потенциальная энергия волнового процесса численно равна работе, совершаемой упругими силами, действующими на выделенный объем

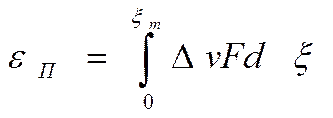(2.14)

Используя для случая твердого тела выражение для силы F и смещения ξ через деформацию ε, приведем уравнение к виду:

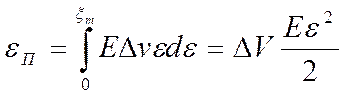. (2.15)

Отсюда плотность потенциальной энергии

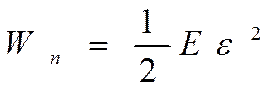, (2.16)

а общая плотность энергии бегущей волны

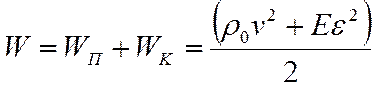(2.17)

Таким образом, плотность энергии в бегущей волне в каждый момент времени равна нулю в местах с наибольшим смещением и максимальна в места, наибольшей по модулю деформации.

По закону сохранения энергии изменения энергии в объеме во времени равно энергии, перешедшей через поверхность, которую можно выразить через работу сил. В этом случае величина Ф = Sσv является потоком энергии, прошедшем через площадки S. Ее удельное значение I = -σv = ρv, называют плотностью потока энергии, или интенсивностью волны (вектор Умова). Для гармонической бегущей волны

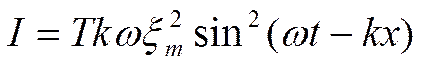(2.18)

Из последнего соотношения следует, что плотность потока энергии равна нулю при наибольшем смещении и максимальна при наибольших значениях скорости и деформации, причем достигаем максимума дважды за период. Направление потока энергии всегда совпадает с направлением распространения волны.

Таким образом, в линейном приближении для волнового процесса характерным является перенос энергии в отсутствии переноса массы. Энергия, передаваемая за большое число периодов может быть определена из среднего значения

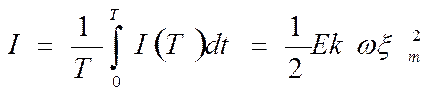(2.19)

Последнее выражение приводится к виду

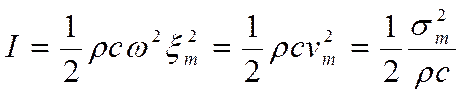, (2.20)

В отличие от бегущей волны в стоячей волне переноса энергии нет. Это обусловлено тем, что в любой момент времени в узлах деформаций и скоростей поток энергии равен нулю. Таким образом, каждый участок длиной в четверть длины волны λ/4, заключенным между двумя ближайшими узлами, не обменивается энергией с соседними участками. Его энергия постоянна. В каждом таком участие дважды за период происходит превращение кинетической энергии, сосредоточенный в основном в местах пучности скоростей в потенциальную, сосредоточенную в пучности деформаций. Следовательно, при скорости равной нулю, энергия целиком потенциальная, а при деформации равной нулю, энергия целиком кинетическая. Энергия ξ на участке 0 ≤ х ≤ λ/4 равна потенциальной энергии в момент v = 0; и cosωt = l; значит

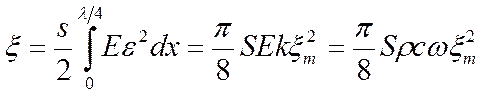. (2.21)