Механической системы
Главным моментом количеств движения механической (кинетическим моментом) называется геометрическая сумма моментов количеств движения материальных точек данной системы:
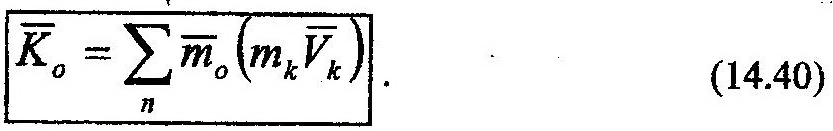
Аналогично (14.40) определяются кинетические моменты системы относительно координатных осей:
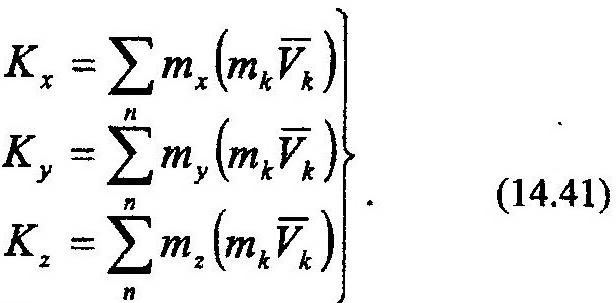
Если количество движения системы, Q, характеризует поступательную составляющую движения механической системы, то кинетический момент, К, - ее угловое перемещение. Очевидно, что выражения (14.40) и (14.41) неудобны для вычисления кинетических моментов, поскольку они подразумевают длительный процесс суммирования. При вращательном движении тела можно предложить удобную форму вычисления данной характеристики.
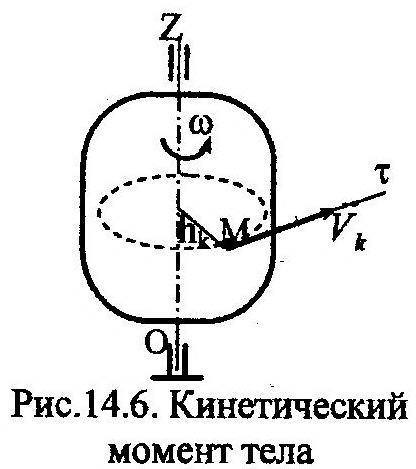
На рис. 14.6 представлено тело, совершающее вращательное движение относительно неподвижной оси z. Найдем Kz для данного случая, для чего запишем момент количества движения произвольной точки М относительно оси z. Получим:
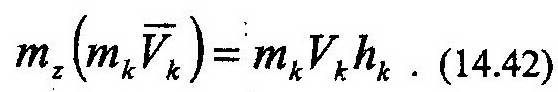
Для достижения цели воспользуемся выражением (14.41). Подставив в него (14.42),
получим:
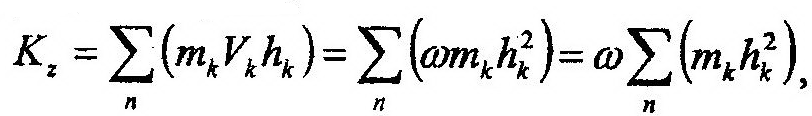 или Kz=Izω (14.43)
или Kz=Izω (14.43)
| 
| ||
| где | 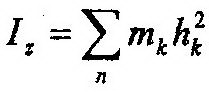
| – осевой момент инерции тела, являющийся | |
| мерой инертности тела при вращательном движении. Нетрудно проследить прямую аналогию между выражениями (14.43) и | |||
(14.18). Действительно, кинетический момент и количество движения являются динамическими характеристиками механической системы. Они определяются как произведение меры инертности на скорость. В случае расчета величины количества движения, характеризующей поступательную составляющую движения системы, используется масса и линейная скорость, а при определении кинетического момента – момент инерции и угловая скорость. Структура этих выражений следующая:

Дата добавления: 2016-12-16; просмотров: 1446;











