Расчёт закрытой конической зубчатой передачи

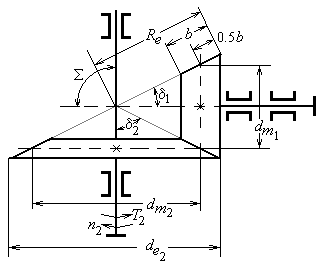Рис. 2.4

Наибольшее применение в редукторостроении получили прямозубые конические колёса, у которых оси валов пересекаются под углом = 90 (рис. 2.4), так называемые ортогональные передачи.

Проектный расчёт.Основной габаритный размер передачи − делительный диаметр колеса по внешнему торцу − рассчитывают по формуле [1]:

,

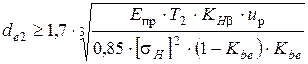где Епр− приведённый модуль упругости, для стальных колёс Епр= Естали=
= 2,1105МПа;

T2− вращающий момент на валу колеса, Нмм (см.п.2.3, с. 26);

KH− коэффициент неравномерности распределения нагрузки по длине зуба, определяют по графикам на рис. 2.5.

Здесь Кbe− коэффициент ширины зубчатого венца относительно внешнего конусного расстояния, Кbe= bw/ Re. Рекомендуют принять Кbe 0,3. Меньшие значения назначают для неприрабатываемых зубчатых колёс, когда H1и H2> 350 HB или V > 15 м/с .

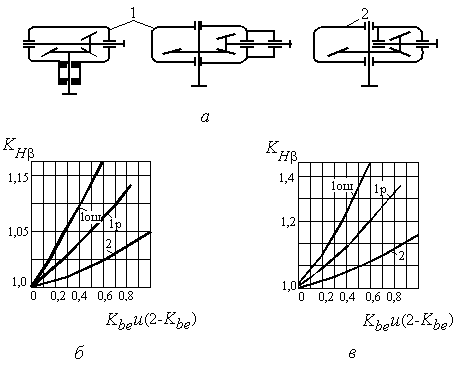
Рис. 2.5

Наиболее распространено в редукторостроении значение Кbe= 0,285, тогда предыдущее выражение для определения делительного диаметра по внешнему торцу колеса принимает вид

,

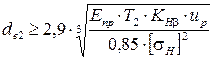где u_p– расчетное передаточное число конической передачи, u_p = tgδ₂ или
u_p = z₂ / z₁.

Геометрический расчёт.Определяют делительный диаметр шестерни по внешнему торцу .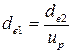

Число зубьев шестерни 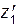назначают по рекомендациям, представленным на рис. 2.6.

По значению 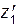определяют число зубьев шестерни:

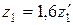при Н1 и Н2 350 HB ,

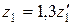при Н1 45 HRC и Н2 350 HB ,

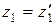при Н1 и Н2 45 HRC .

Вычисленное значение z1 округляют до целого числа.

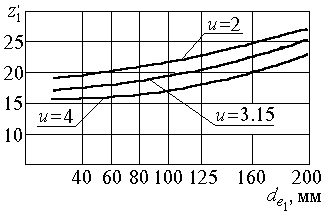
Рис. 2.6

Определяют число зубьев колеса .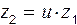

Вычисленное значение 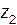округляют до целого числа. После этого необходимо уточнить:

- передаточное число передачи ,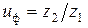

- угол делительного конуса колеса ,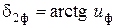

- угол делительного конуса шестерни ,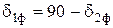

- внешний окружной модуль .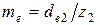

Рекомендуется округлить m_e до стандартного значения m_eф по ряду модулей: 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10. После этого уточняют величины диаметров 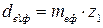и .

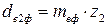Рассчитывают величину внешнего конусного расстояния передачи
(рис. 2.4) .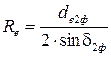

Рабочая ширина зубчатого венца колеса определяют как .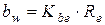

Полученное значение 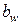округляют до ближайшего из ряда нормальных линейных размеров (табл. 2.5).

Определяют расчётный модуль зацепления в среднем сечении зуба

.

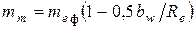При этом найденное значение m_m не округляют!

Рассчитывают внешнюю высоту головки зуба .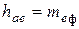

Внешнюю высоту ножки зуба определяют как .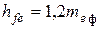

Внешний диаметр вершин зубьев колёс рассчитывают по формуле

.

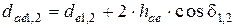Угол ножки зуба рассчитывают по формуле .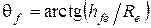

Проверочный расчёт.При расчёте на выносливость зубьев колёс по контактным напряжениям проверяют выполнение условия

,

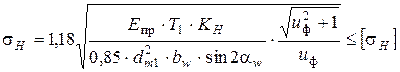где Eпр− приведённый модуль упругости, для стальных колёс Eпр= Eстали=
= 2,1105МПа ;

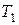− вращающий момент на шестерне, Нмм, ;

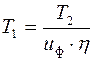здесь 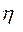− КПД передачи.

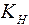− коэффициент расчётной нагрузки, 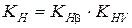; коэффициент концентрации нагрузки 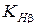найден ранее по графикам рис. 2.5.

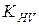− коэффициент динамической нагрузки, находят по табл. 2.7 с понижением на одну степень точности против фактической, назначенной по окружной скорости 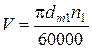в соответствии с рекомендациями (табл. 2.6);

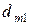− делительный диаметр шестерни в среднем сечении зуба,

;

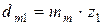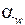− угол зацепления, 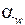=20 .

Далее проверяют зубья колёс на выносливость по напряжениям изгиба по формулам [1]:

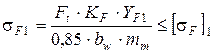и ,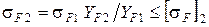

где 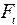− окружное усилие в зацеплении, Н, ;

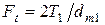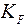− коэффициент расчётной нагрузки, K_F = K_Fb ∙ K_FV. Здесь
K_Fb = 1 + 1,5 ∙ (K_Hb − 1), а 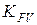определяют по табл. 2.7 с понижением точности на одну степень против фактической.

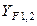− коэффициент формы зуба соответственно шестерни и колеса, находят по табл. 2.9 в зависимости от эквивалентного числа зубьев колёс

.

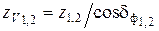2.8. Проектный расчёт открытой конической прямозубой
передачи

Модуль зацепления в среднем сечении зуба конического колеса рассчитывают по формуле

,

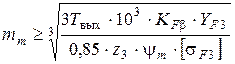где, кроме рассмотренных выше величин (см. п. 2.6), рекомендуют назначить
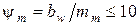и 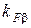=1,1…1,2.

Далее рассчитывают основные геометрические параметры зубчатых колёс открытой передачи:

− ширину зубчатого венца 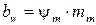(с округлением до целого числа по ряду нормальных линейных размеров);

− делительный диаметр в среднем сечении зуба шестерни ;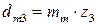

− по заданному (или принятому) передаточному числу uотк находим угол при вершине делительного конуса ;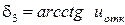

− среднее конусное расстояние ;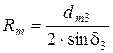

− внешнее конусное расстояние ;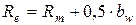

− модуль зацепления на внешнем торце ;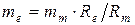

− внешний делительный диаметр шестерни .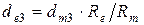

Проверочный расчет такой передачи на выносливость по контактным напряжениям выполняют в соответствии с п. 2.7 («Расчет закрытой конической зубчатой передачи»).

3. ПРОЕКТНЫЙ РАСЧЕТ ВАЛОВ И ОПОРНЫХ
КОНСТРУКЦИЙ

В различных узлах машин (в том числе в механических передачах) содержится ряд деталей, предназначенных для поддерживания вращающихся элементов зубчатых и червячных колёс, шкивов, звёздочек и т.д. Такие детали называются валами и осями. По конструкции оси и прямые валы мало отличаются друг от друга, но характер их работы существенно различен: оси являются поддерживающими деталями и воспринимают только изгибающие нагрузки; валы представляют собой звенья механизмов, передающие крутящие моменты и, помимо изгиба, испытывают кручение.

Нагрузки, воспринимаемые валами и осями, передаются на корпуса, рамы и станины через опорные устройства подшипники.

Части валов и осей, непосредственно соприкасающиеся с подшипниками, носят общее наименование «цапфы». Цапфу, расположенную на конце вала, называют шипом, а цапфу на средней части вала шейкой. Цапфы, передающие на опоры осевые нагрузки, называют пятами.

Оси могут быть неподвижными или вращаться вместе с насаженными на них деталями. Валы при работе механизма всегда вращаются.

Признаками для классификации валов служат их назначение, форма геометрической оси, конструктивные особенности.

Основными критериями работоспособности проектируемых редукторных валов являются прочность и выносливость. Они испытывают сложную деформацию совместное действие кручения, изгиба и растяжения (сжатия). Но так как напряжения в валах от растяжения небольшие, то их обычно не учитывают.

Расчёт редукторных валов производится в два этапа:

1-й проектный (приближённый) расчёт валов на чистое кручение;

2-й проверочный (уточнённый) расчёт валов на выносливость по напряжениям изгиба и кручения.