Поверхностная энергия и поверхностное натяжение.

Поверхностный слой, возникающий на границе различных фаз, следует рассматривать как самостоятельную фазу толщиной в несколько молекул. В отдельных случаях поверхностный слой имеет толщину, равную диаметру молекулы, и его называют мономо­лекулярным.Поэтому поверхностный слой нужно рассматривать как микрогетерогенную систему.

Поверхностный слой резко отличается по своим свойствам от свойств фаз, которые он разделяет. Молекулы, атомы, ионы, нахо­дящиеся на границе раздела фаз, не равноценны тем же частицам, находящимся в объеме фазы.

Силы, действующие на молекулы, находящиеся внутри жид­кости, одинаковы со всех сторон, и их равнодействующая F равна нулю. Силы, действующие на молекулы повехностного слоя грани­цы раздела жидкости с ее паром, не одинаковы со стороны раствора (снизу и с боков) и газообразной фазы (сверху). Молекулярные взаимодействия сверху отсутствуют, равнодействущая сил F не равна нулю и направлена внутрь жидкой фазы (рис. 22). Для вы­хода молекул на поверхность требуется выполнить работу Ws про­тив этой силы. В итоге формируется поверхностный слой с избы­точной поверхностной энергией Гиббса G_s.

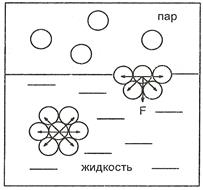
Рис. 22.Взаимодействие между молекулами в объеме жидкости и в поверхностном слое.

Все возможные поверхности раздела в зависимости от агрегат­ного состояния граничащих фаз делят на подвижные поверхности раздела между жидкостью и газом (ж-г), двумя несмешивающимися жидкостями (ж-ж) и неподвижные поверхности раздела между твердым телом и газом (т-г), твердым телом и жидкостью (т-ж), твердым телом и твердым телом (т-т).

При измельчении какой-либо твердой или жидкой фазы суммар­ный объем и масса остаются теми же самыми, тогда как суммарная площадь поверхности раздела возрастает.

Чтобы учесть влияние поверхности на свойства системы, вво­дят понятие удельной поверхности(S_ya) фазы - величины, измеряемой суммарной площадью граничной поверхности фазы (S_cyM), отнесенной к ее объему (V):

Sуд = Sсум/V

Влияние поверхности раздела фаз на свойства системы воз­растает с увеличением удельной поверхности.

Энергия Гиббса G системы из двух фаз состоит из двух сла­гаемых - энергии Гиббса объемных фаз Gv и поверхностной энер­гии Гиббса G_S:

G = G_V + G_S.

Энергия Гиббса объемных фаз пропорциональна их массе, а, следовательно, объему, занимаемому системой:

G_V = kV.

Поверхностная энергия Гиббса системы пропорциональна меж­фазной поверхности:

G_V = σS,

где σ- коэффициент пропорциональности, называемый поверх­ностным натяжением. Его величину измеряют в кДж/м² (Н/метр) или в Дж/см².

Поверхностное натяжение σ есть величина, измеряемая энергией Гиббса, приходящейся на единицу площади поверхностно­го слоя. Оно численно равно работе, которую необходимо совер­шить в данной системе для образования в ней единицы поверхности раздела фаз при постоянной температуре.

С учетом предыдущего получим уравнение:

G = kV + σ S

G/V= k + σ S_уд.

Следовательно, энергия Гиббса, приходящаяся на единицу объ­ема системы, линейно увеличивается с увеличением ее удельной поверхности. При малых значениях удельной поверхности S_yд. по­верхностной энергией Гиббса можно пренебречь. При больших зна­чениях S_уд. с ней необходимо считаться.

Если поверхность кожи человека составляет 1.5 м², то поверх­ность эритроцитов имеет величину уже 3000м². Трудно оценить величину суммарной поверхности, разделяющей все клетки орга­низма, если помнить, что их общее число составляет около 10¹⁴, а к ним еще следует добавить микроорганизмы кишечной флоры, ко­личество которых больше, чем общее количество клеток организма. Организм представляет собой совокупность систем с сильно развитыми поверхностями раздела (кожные покровы, стенки кровеносных сосудов, оболочки органов, клеточные мембраны, мембраны органелл, то есть клеточных структур и т. д.). В живых системах, следовательно, величина поверхностной энергии должна иметь большую величину.

Поверхностное натяжение различных жидкостей на границе жидкость - газ возрастает с увеличением взаимодей­ствия между молекулами жидкости, являясь максимальным для во­ды из числа веществ, представленных в табл. 23.

Таблица 23