Оценка систематической погрешности

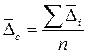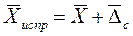, _, (2.9.)

Считая Х, sслучайными величинами, возникает вопрос о точности получения этих оценок, которые определяются следующим образом:

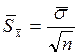- оценка погрешности получения (1.10.)

среднего значения результата измерения Х,

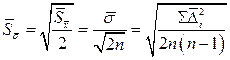
(1.11.)

- оценка погрешноти получения s ( ср.-квадратич. отклонения)

Таким образом, можно записать результат измерения по оценкам измерения ® _,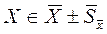

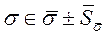
вторая оценка, которая применима, если измеряемая величина Х- неизвестна, n - мало(ограниченно).

В этом случае для надежной оценки результатов измерения используют доверительный интервал -- I_д=(x+e, x-e)и доверительную вероятность --Р_д (D, n),где

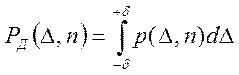
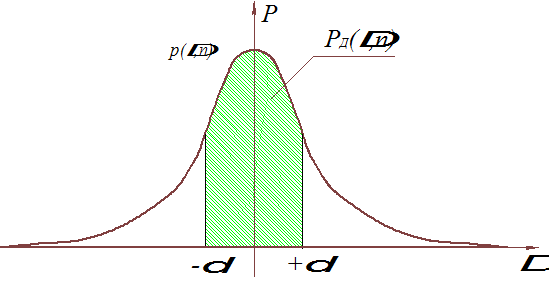
Рис 1.5. Здесь p(D,n)-- плотность вероятности, d- границы доверительного интервала.

Под доверительной вероятностью (Р_д)понимают вероятность появления погрешности, не выходящей за некоторые принятые границы ( 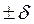), интервал этих границ называют доверительным интервалом (I_д)

Для этих оценок наиболее применимо известное в практике t_n-распределление (или распределение Стьюдента), введенное в 1908 году В.С. Госсетом, носившим псевдоним - Стьюдент. Это распределение приn®¥приближается к нормальному распределению. Для использования на практике t_n(n,P_д)-распределениесведены в таблицу , называемую коэффициентами t_n-распределения Стьюдента, в виде

Рд n-1	0,5	0,7	0,8	0,9	0,99
n
	1,0	1,963	3,078	6,314	66,657
	0,718	1,134	1,44	1,943	3,707
	0,7	1,093	1,372	1,812	3,169
	0,687	1,064	1,325	1,725	2,845
	0,683	1,055	1,31	1,697	2.75
¥	0,67449	1,03643	1,28155	1,64485	2,576

Используя коэфф.t_n(n,P_д)можно определить доверительный интервал

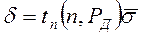(1.12)

для вероятностей ,полученных согласно распределению Стьюдента.

Например: , , .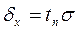

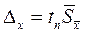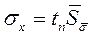Таким образом, результаты измерения следует записывать

х Î ( х_ср ± d_x , s_x , P_д , n )