Классификация измерений

Понятия об измерениях и измерительных средстствах

Измерением называют нахождение значения физической величины опытным путем с помощью технических средств. Измерить какую либо величину - значит сравнить ее с другой, выбранной за единицу измерения (меру, эталон и т.п.), т.е. количественно определить ее величину и погрешность измерения.

Качество измерений характеризуется точностью, достоверностью, сходимостью и воспроизводимостью измерений.

В процессе измерений участвуют объект измерения, измерительное средство, анализирующее устройство(с оператором и без) и внешняя среда, в которой находится объект измерения (Рис1.1.).

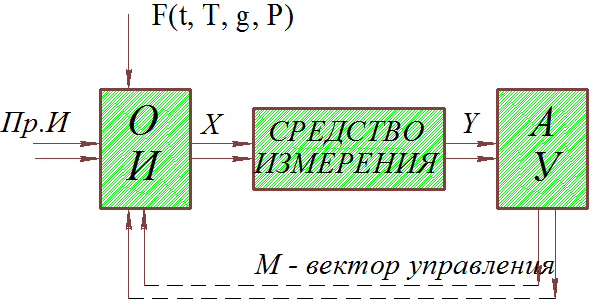
Рис.1.1 Обобщенная структура алгоритма измерения

Пр.И - программа измерений ,OИ - объект измерения,

АУ -анализирующее устройство , F(t, T, g, P) -вектор возмущения,X -вектор измеряемых параметров, Y -вектор измерительной информации,t-время ;g-ускорение,T -температура,P -давление среды, где находится ОИ.

Объектом измерения являются физические величины , характеризующие свойства реальных объектов , их состояний или протекающих в них процессов. Например: температурное поле какой - либо среды, технические параметры космического телескопа.

К средствам измерения принято относить : меру,измеритель -преобразователь(И-П), измерительный прибор(ИП), измерительную установку(ИУ), измерительную систему(ИС), измерительный информационный комплекс (ИИК)(Рис.2.2).

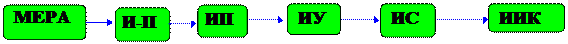Рис.1.2. Состав измерительных средств, где стрелками показано,что предыдущие средства измерения включаются в последующие.

Классификация измерений

Оптические измерения классифицируются следующим образом:

по виду и методам измерений,поспособу выражения результатов измерений,похарактеру измеряемой величины,повиду воздействия на объект измерения.

1.2.1. По виду измерений:

Прямыми измерениями называют, когда измеряемая величина находится в непосредственных единицах измерения. Например: измерение углов на гониометре в угл. мере, измерение размеров микрометром в мкм.

Косвенными измерениями - когда измеряется не сама величина, а другие , связанные с ней определенной функциональной зависимостью

y=¦(х_1,,х₂,...), например: радиус кривизны сферической поверхности определяется по формуле R=(r²+h²)/ 2h , где r - радиус измерительного кольца, h- высота сегмента сферы.

Рис 1.3

Совместные и совокупныеизмерения применяются для увеличения точности измерений, в этих случаях одну или несколько искомых величин измеряют несколько раз, при этом меняют или условия измерения (совместные измерения) или меняют сочетания измеряемых величин (совокупные измерения). В результате измерений составляется система уравнений, связывающая искомые и измеряемые величины, решая которую находим истинные величины.

Примеры . 1.совокупные измерения.Измерение погрешности изготовле ния трех плоских зеркал, которые накладываются друг на друга.

По интерференционной картине, которая образуется при этом составляются уравнения: N₁=Х₁+Х₂, N₂=Х₁+Х_{3 ,} N₃=Х ₂+Х₃,где N_i -число видимых интерференционных полос ,образованных парами плоских зеркал. Решая эти уравнения, получим Х_i- искомое число интерференционных полос.

2.Совместные измерения. Измерения плоскостности зеркал двумя и более методами или разными условиями измерения, где также составляются аналогичные уравнения: N₁=Х₁+Х₂, N₂=Х₁+Х₂.