ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ 6 глава
Кинетическая энергия вращающегося тела есть сумма кинетических энергий его точек, т.е.
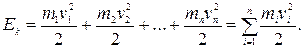
Учитывая связь между угловой и линейной скоростями, получим:
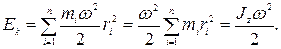 (4.9)
(4.9)
Сопоставление формулы (4.9) с выражением для кинетической энергии тела, движущегося поступательно со скоростью v, показывает, что момент инерции является мерой инертности тела во вращательном движении.
Если твердое тело движется поступательно со скоростью v и одновременно вращается с угловой скоростью ω вокруг оси, проходящей через его центр инерции, то его кинетическая энергия определяется как сумма двух составляющих:
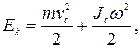 (4.10)
(4.10)
 где vc – скорость центра масс тела; Jc - момент инерции тела относительно оси, проходящей через его центр масс.
где vc – скорость центра масс тела; Jc - момент инерции тела относительно оси, проходящей через его центр масс.
Моментом силы относительно неподвижной осиz называется скалярная величина Mz, равная проекции на эту ось вектора 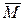 момента силы, определенного относительно произвольной точки 0 данной оси. Значение момента Mz не зависит от выбора положения точки 0 на оси z.
момента силы, определенного относительно произвольной точки 0 данной оси. Значение момента Mz не зависит от выбора положения точки 0 на оси z.
Если ось z совпадает с направлением вектора 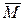 , то момент силы представляется в виде вектора, совпадающего с осью:
, то момент силы представляется в виде вектора, совпадающего с осью:
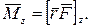
Найдем выражение для работы при вращении тела. Пусть сила 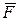 приложена к точке В, находящейся от оси вращения на расстоянии r (рис. 4.6); α – угол между направлением силы и радиусом-вектором
приложена к точке В, находящейся от оси вращения на расстоянии r (рис. 4.6); α – угол между направлением силы и радиусом-вектором 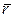 . Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.
. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.
 При повороте тела на бесконечно малый угол
При повороте тела на бесконечно малый угол 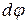 точка приложения В проходит путь
точка приложения В проходит путь 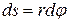 , и работа равна произведению проекции силы на направление смещения на величину смещения:
, и работа равна произведению проекции силы на направление смещения на величину смещения:
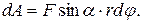
Учитывая, что 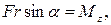 можно записать
можно записать 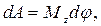 где Mz - момент силы относительно оси вращения. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
где Mz - момент силы относительно оси вращения. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
Работа при вращении тела идет на увеличение его кинетической энергии:
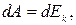
где 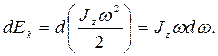 Тогда
Тогда 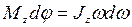 , или
, или 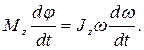 Учитывая, что
Учитывая, что 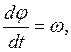 получим
получим
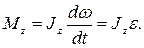 (4.11)
(4.11)
Уравнение (4.11) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
4.4. Закон сохранения момента импульса
Моментом импульса относительно неподвижной осиz называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса Lz не зависит от положения точки 0 на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса 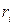 с некоторой скоростью
с некоторой скоростью 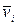 . Скорость
. Скорость 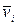 и импульс
и импульс 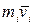 перпендикулярны этому радиусу, т.е. радиус является плечом вектора
перпендикулярны этому радиусу, т.е. радиус является плечом вектора 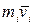 . Поэтому можно записать, что момент импульса отдельной точки относительно оси z равен
. Поэтому можно записать, что момент импульса отдельной точки относительно оси z равен
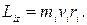
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его точек:
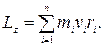
Учитывая связь между линейной и угловой скоростями ( 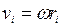 ), получим следующее выражение для момента импульса тела относительно неподвижной оси:
), получим следующее выражение для момента импульса тела относительно неподвижной оси:
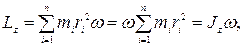 (4.12)
(4.12)
т.е. момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцировав выражение (4.12) по времени, получим:
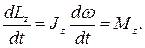 (4.13)
(4.13)
Это еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: скорость изменения момента импульса тела относительно неподвижной оси вращения равна результирующему моменту относительно этой оси всех внешних сил, действующих на тело.
Закон сохранения момента импульса вытекает из основного уравнения динамики вращательного движения тела, закрепленного в неподвижной точке (уравнение 4.8), и состоит в следующем:
если результирующий момент внешних сил относительно неподвижной точки тождественно равен нулю, то момент импульса тела относительно этой точки с течением времени не изменяется.
Действительно, если 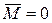 , то
, то 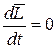 , откуда
, откуда
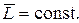 (4.14)
(4.14)
Другими словами, момент импульса замкнутой системы с течением времени не изменяется.
Из основного закона динамики тела, вращающегося вокруг неподвижной оси z (уравнение 4.13), следует закон сохранения момента импульса тела относительно оси:
если момент внешних сил относительно неподвижной оси вращения тела тождественно равен нулю, то момент импульса тела относительно этой оси не изменяется в процессе движения, т.е. если Mz=0, то 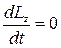 , откуда
, откуда
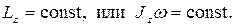 (4.15)
(4.15)
Закон сохранения момента импульса является фундаментальным законом природы. Справедливость этого закона обусловливается свойством симметрии пространства – его изотропностью, т.е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета.
Справедливость закона сохранения момента импульса относительно неподвижной оси вращения можно продемонстрировать на опыте со скамьей Жуковского. Скамьей Жуковского называется горизонтальная площадка, свободно вращающаяся без трения вокруг неподвижной вертикальной оси ОО1. Человек, стоящий или сидящий на скамье, держит в вытянутых руках гимнастические гантели и приводится во вращение вместе со скамьей вокруг оси ОО1 с угловой скоростью 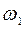 . Приближая гантели к себе, человек уменьшает момент инерции системы, а так как момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость ее вращения
. Приближая гантели к себе, человек уменьшает момент инерции системы, а так как момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость ее вращения 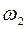 возрастает. Тогда по закону сохранения момента импульса относительно оси ОО1 можно записать:
возрастает. Тогда по закону сохранения момента импульса относительно оси ОО1 можно записать:
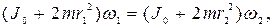 (4.16)
(4.16)
где 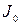 - момент инерции человека и скамьи;
- момент инерции человека и скамьи; 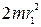 и
и 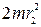 - моменты инерции гантелей в первом и втором положениях; m – масса одной гантели; r1, r2 – расстояния от гантелей до оси ОО1.
- моменты инерции гантелей в первом и втором положениях; m – масса одной гантели; r1, r2 – расстояния от гантелей до оси ОО1.
Изменение момента инерции системы связано с изменением ее кинетической энергии:
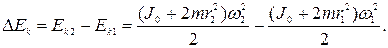
Используя выражение для 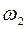 , полученное из (4.16)
, полученное из (4.16)
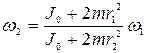 ,
,
после преобразований получим:
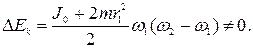
Это изменение кинетической энергии системы численно равно работе, совершенной человеком при перемещении гантелей.
В табл. 4.2 сопоставлены основные физические величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение.
Таблица 4.2
| Поступательное движение | Вращательное движение |
| Масса m | Момент инерции Jz |
Скорость 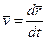
| Угловая скорость 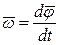
|
Ускорение 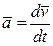
| Угловое ускорение 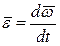
|
Сила 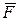
| Момент силы 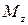
|
Импульс 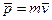
| Момент импульса 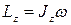
|
Основное уравнение динамики:
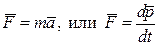
| Основное уравнение динамики:
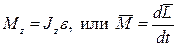
|
Работа 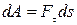
| Работа вращения 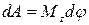
|
Кинетическая энергия 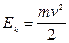
| Кинетическая энергия вращения
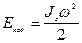
|
Краткие выводы
· Вращательным называется движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения.
· Момент инерции тела относительно оси вращения – это физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси:
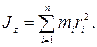
· Момент инерции тела Jz относительно любой оси вращения равен моменту его инерции Jc относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы m тела на квадрат расстояния а между осями:
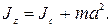
· При вращении абсолютно твердого тела вокруг неподвижной оси z его кинетическая энергия равна половине произведения момента инерции относительно оси вращения на квадрат угловой скорости:
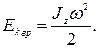
· Из сравнения формул 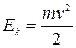 и
и 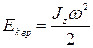 следует, что момент инерции – мера инертности тела при вращательном движении.
следует, что момент инерции – мера инертности тела при вращательном движении.
· Работа вращения тела идет на увеличение его кинетической энергии и определяется выражением 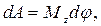 где Mz – момент сил относительно оси вращения z.
где Mz – момент сил относительно оси вращения z.
· Уравнение динамики вращательного движения твердого тела относительно неподвижной оси z (аналог второго закона Ньютона) имеет вид:
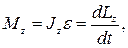
где Lz – момент импульса твердого тела относительно оси z.
· В замкнутой механической системе момент внешних сил относительно неподвижной оси Mz=0 и 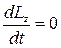 , откуда Lz=const – закон сохранения момента импульса. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.
, откуда Lz=const – закон сохранения момента импульса. Он является следствием изотропности пространства: инвариантность физических законов относительно выбора направления осей координат системы отсчета.
Вопросы для самоконтроля и повторения
1. Что называется моментом инерции тела? Какова роль момента инерции во вращательном движении?
2. Сформулируйте теорему Штейнера. От чего зависит момент инерции тела?
3. Что называется моментом силы относительно неподвижной точки? Относительно неподвижной оси? Как определяется направление момента силы?
4. Что такое момент импульса твердого тела? Как определяется направление момента импульса?
5. Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси? Как определяется работа при вращении тела?
6. Выведите и сформулируйте уравнение динамики вращательного движения твердого тела.
7. Сформулируйте закон сохранения момента импульса. В каких системах он выполняется?
8. Сопоставьте основные величины и уравнения динамики поступательного и вращательного движений.
Примеры решения задач
Задача 1. Шар радиусом 10 см и массой 5 кг вращается вокруг оси симметрии по закону 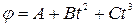 , где В=2 рад/с2, С=-0,5 рад/с3. Определить момент сил относительно оси вращения для момента времени t=3 c.
, где В=2 рад/с2, С=-0,5 рад/с3. Определить момент сил относительно оси вращения для момента времени t=3 c.
Дано: R=0,1 м; m=5 кг; 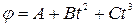 рад; В=2 рад/с2; С=-0,5 рад/с3; t=3 c.
рад; В=2 рад/с2; С=-0,5 рад/с3; t=3 c.
Найти: Mz.
Решение
Согласно уравнению динамики вращательного движения твердого тела относительно неподвижной оси
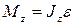 , где
, где 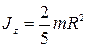 - момент инерции шара;
- момент инерции шара;
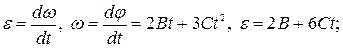
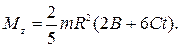
Для t=3 c 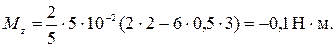
Ответ: Mz=-0,1 Н·м.
 Задача 2. На однородный сплошной цилиндрический вал радиусом 20 см, момент инерции которого 0,15 кг·м2, намотана легкая нить, к концу которой прикреплен груз массой 0,5 кг. До начала вращения барабана высота груза над полом составляла 2,3 м (рис. ). Определить: а) время опускания груза до пола; б) силу натяжения нити; в) кинетическую энергию груза в момент удара о пол.
Задача 2. На однородный сплошной цилиндрический вал радиусом 20 см, момент инерции которого 0,15 кг·м2, намотана легкая нить, к концу которой прикреплен груз массой 0,5 кг. До начала вращения барабана высота груза над полом составляла 2,3 м (рис. ). Определить: а) время опускания груза до пола; б) силу натяжения нити; в) кинетическую энергию груза в момент удара о пол.
Дано: R=0,2 м; Jz=0,15 кг·м2; m=0,5 кг; h=2,3 м.
Найти: t, T, Eк. 
Решение
По закону сохранения энергии

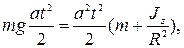 откуда
откуда 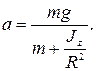
Время опускания груза до пола:

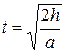 .
.
Уравнение динамики вращательного движения вала 
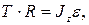 откуда сила натяжения нити
откуда сила натяжения нити
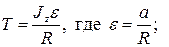 тогда
тогда 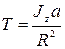 .
.
Кинетическая энергия груза в момент удара о пол:
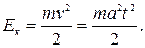
Ответ: t=2 с; Т=4,31 Н; Ек=1,32 Дж.
Задачи для самостоятельного решения
1. Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.
2. Полый тонкостенный цилиндр массой 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену 1,4 м/с, после удара 1 м/с. Определить выделившееся при ударе количество теплоты.
3. К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определить кинетическую энергию через 4 с после начала действия силы.
4. Вентилятор вращается с частотой 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав 50 оборотов, остановился. Работа сил торможения равна 31,4 Дж. Определить: а) момент сил торможения; б) момент инерции вентилятора.
5. К ободу однородного сплошного диска радиусом 0,5 м приложена постоянная касательная сила 100 Н. При вращении диска на него действует момент сил трения 2 Н·м. Определить массу диска, если известно, что его угловое ускорение постоянно и равно 16 рад/с2.
6. С наклонной плоскости, составляющей угол 300 с горизонтом, скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см.
7. На однородный сплошной цилиндрический вал радиусом 50 см намотана легкая нить, к концу которой прикреплен груз массой 6,4 кг. Груз, разматывая нить, опускается с ускорением 2 м/с2. Определить: а) момент инерции вала; б) массу вала.
8. Горизонтальная платформа массой 25 кг и радиусом 0,8 м вращается с частотой 18 об/мин. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от 3,5 кг·м2 до 1 кг·м2.
9. Человек массой 60 кг, стоящий на краю горизонтальной платформы массой 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10 об/мин, переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить, с какой частотой будет тогда вращаться платформа.
10. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.
ГЛАВА 5. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ
ОТНОСИТЕЛЬНОСТИ
5.1. Механический принцип относительности
и законы электродинамики
 Во второй половине XIX века Д. Максвеллом были сформулированы основные законы электродинамики. При этом возникли сомнения в справедливости механического принципа относительности Галилея применительно к электромагнитным явлениям. Вспомним суть механического принципа относительности.
Во второй половине XIX века Д. Максвеллом были сформулированы основные законы электродинамики. При этом возникли сомнения в справедливости механического принципа относительности Галилея применительно к электромагнитным явлениям. Вспомним суть механического принципа относительности.
Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму (инвариантны); в этом состоит суть механического принципа относительности или принципа относительности Галилея.
Для доказательства этого принципа рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), которую условно будем считать неподвижной и подвижную систему 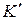 (с координатами
(с координатами 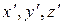 ), движущуюся относительно К равномерно и прямолинейно со скоростью
), движущуюся относительно К равномерно и прямолинейно со скоростью 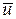 = const. Примем, что в начальный момент времени t = 0 начала О и
= const. Примем, что в начальный момент времени t = 0 начала О и 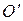 обеих систем координат совпадают. Расположение систем координат в произвольный момент времени t имеет вид, изображенный на рис. 5.1. Скорость
обеих систем координат совпадают. Расположение систем координат в произвольный момент времени t имеет вид, изображенный на рис. 5.1. Скорость 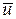 направлена вдоль прямой
направлена вдоль прямой 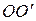 , а радиус-вектор, проведенный из точки О в точку
, а радиус-вектор, проведенный из точки О в точку 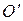 , равен
, равен 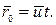
Координаты произвольной материальной точки А в неподвижной и подвижной системах отсчета определяются радиусами-векторами 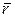 и
и 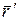 , причем
, причем
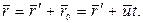 (5.1)
(5.1)
В проекциях на оси координат векторное уравнение (5.1) записывается в виде, называемом преобразованиями Галилея:
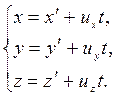 (5.2)
(5.2)
В частном случае, когда система 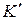 движется со скоростью
движется со скоростью 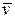 вдоль положительного направления оси х системы К, преобразования координат Галилея имеют следующий вид:
вдоль положительного направления оси х системы К, преобразования координат Галилея имеют следующий вид:
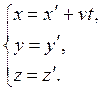
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета. Поэтому система уравнений (5.2) дополняется еще одним соотношением:
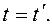 (5.3)
(5.3)
Соотношения (5.2) – (5.3) справедливы лишь в случае 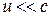 . При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.
. При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.
Продифференцируем уравнение (5.1) по времени и учитывая, что 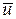 =const, найдем соотношения между скоростями и ускорениями точки А относительно обеих систем отсчета:
=const, найдем соотношения между скоростями и ускорениями точки А относительно обеих систем отсчета:
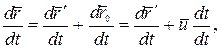
откуда
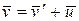 , (5.4)
, (5.4)
а также
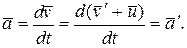 (5.5)
(5.5)
Если на точку А другие тела не действуют, то 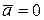 и согласно (5.5)
и согласно (5.5) 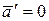 , т.е. подвижная система К΄ является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.
, т.е. подвижная система К΄ является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.
Из выражения (5.5) следует, что
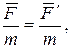 или
или 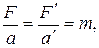
т.е. уравнения Ньютона (уравнения динамики) для материальной точки одинаковы во всех инерциальных системах отсчета или инвариантны по отношению к преобразованиям Галилея. Этот результат часто формулируют следующим образом: равномерное и прямолинейное движение системы как целого не влияет на ход протекающих в ней механических процессов.
Классическая механика Ньютона достоверно описывает движение макроскопических тел, движущихся со скоростями, намного меньшими скорости света. В конце XIX в. было установлено, что выводы классической механики противоречат некоторым опытным данным. В частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам Ньютона. Далее возникли затруднения при попытках применить классическую механику для объяснения распространения света. Согласно законам электродинамики скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и приблизительно равна с = 3·108 м/с. Но в соответствии с законами классической физики скорость света может равняться с только в одной избранной системе отсчета. В любой другой системе отсчета, движущейся относительно избранной системы со скоростью v, она должна уже равняться c-v, или c+v. Это означает, что если справедлив закон сложения скоростей классической механики (формула (5.4)), то при переходе от одной инерциальной системы к другой законы электродинамики должны меняться, так как должна меняться скорость света. Таким образом, обнаружились противоречия между электродинамикой и механикой Ньютона, законы которой согласуются с принципом относительности Галилея. Для преодоления возникших трудностей предлагались различные способы:
1. Принять несостоятельность принципа относительности применительно к электромагнитным явлениям. Еще со времен Фарадея электромагнитные явления рассматривались как процессы в особой, всепроникающей среде, заполняющей все пространство, - эфире. Согласно Х. Лоренцу инерциальная система отсчета, покоящаяся относительно эфира, - это особая система, в которой законы электродинамики Максвелла справедливы. Лишь в этой системе отсчета скорость света в вакууме одинакова по всем направлениям.
2. Считать ошибочными уравнения электродинамики Максвелла и попытаться изменить их таким образом, чтобы они при переходе от одной инерциальной системы к другой (в соответствии с классическими представлениями о пространстве и времени) не менялись. Такая попытка, в частности, была предпринята Г. Герцем, который считал, что эфир полностью увлекается движущимися телами, поэтому электромагнитные явления протекают одинаково, независимо от того, покоится тело или движется. Принцип относительности справедлив.
3. Отказаться от классических представлений о пространстве и времени, с тем, чтобы сохранить и принцип относительности, и законы Максвелла. С этой точки зрения оказываются неточными не уравнения электромагнитного поля, а законы механики Ньютона, согласующиеся со старыми представлениями о пространстве и времени. Таким образом, изменять нужно законы классической механики, а не законы электродинамики Максвелла.
Вспомним, как трактовались пространство и время в классической физике. Пространство рассматривалось как бесконечная пустая протяженность, вмещающая в себе все тела и не зависящая от материи. Время рассматривалось как абсолютный фактор равномерного потока длительности, в котором все возникает и исчезает. При этом время не зависит ни от каких процессов в мире.
Развитие естествознания опровергло эти представления. Никакого абсолютного пространства и времени не существует. Вселенная заполнена материей в форме вещества и поля, а пространство выступает как всеобщее свойство материи. Время всегда связано с движением и развитием материи. Таким образом, пространство – это форма бытия материи, которая выражает ее протяженность и структурность; время – это форма бытия материи, характеризующая длительность существования всех объектов, полей и последовательность смены событий.
Дата добавления: 2016-12-16; просмотров: 1888;











