Особенности программирования арифметических и математических функций в LAD и FBD
Арифметические функции представляются в программах блочными элементами. Пример арифметического блочного элемента для функции суммирования данных типа INT приведен на рисунке 2.23.
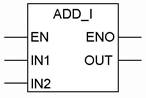
Рисунок 2.23 - Обозначение блочного элемента суммирования данных типа INT
В таблице 2.6 приведены обозначения арифметических функций в соответствии с типом данных.
Блочный элемент арифметической функции кроме входа разрешения EN (enable input) и выхода разрешения ENO (enable output) имеет два входа IN1 и IN2, а также выход OUT. Заголовок в блочном элементе идентифицирует арифметическое действие, которое выполняется.
Таблица 2.6 - Обозначение арифметических функций
| Арифметическая функция | Соответствие типа данных | ||
| INT | DINT | REAL | |
| Добавление | ADD_I | ADD_DI | ADD_R |
| Вычитание | SUB_I | SUB_DI | SUB_R |
| Умножение | MUL_I | MUL_DI | MUL_R |
| Деление (результат – частица) | DIV_I | DIV_DI | DIV_R |
| Деление с остатком | - | MOD_DI | - |
Значения, которые вычисляются, подаются на входы IN1 и IN2, результат вычисления выводится на выход OUT. Используемые переменные должны быть того самого типа данных, что и входы элемента.
Арифметическая функция выполняется, если на входе разрешения присутствует сигнал «1». Если во время вычисления возникает ошибка, то выход разрешения устанавливается в «0. Если выполнение функции не разрешено (EN = 0), то вычисление не выполняется. Если главное реле управления (MCR) активировано, то выход OUT устанавливается в нуль.
Во время выполнения арифметической функции могут возникнуть следующие ошибки:
• переполнение в вычислениях с типами INT и DINT;
• исчезновение значащих разрядов и переполнения в вычислениях с типом REAL;
• недопустимое число REAL в вычислениях с типом REAL.
Пример вычисления данных типа INT
На рисунке 2.24 значение слова в памяти меркеров MW 100 делится на 250, целочисленный результат хранится в меркере MW 102.
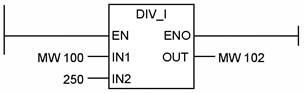
Рисунок 2.24 - Пример применения функции деления чисел INT
Арифметический блочный элемент может быть помещен в любом месте цепи. Прямое соединение с левой (питательной) направляющей позволяет подключить арифметические блочные элементы параллельно. При этом блочные элементы самой верхней цепи обрабатываются слева направо, потом слева направо обрабатываются элементы второй цепи и так далее. Для завершения цепи нужно установить катушку, которой можно назначить, например, бит временных локальных данных.
Если выход ENO предыдущего блочного элемента соединен с входом EN следующего, то последний срабатывает только тогда, когда предыдущий элемент был обработан без ошибок.
Математические функции
В LAD и FBD представлены следующие математические функции:
• синус, косинус, тангенс;
• арксинус, арккосинус, арктангенс;
• возведение в квадрат, извлечение квадратного корня;
• экспонентная функция по основанию е, натуральный логарифм.
Все математические функции работают с числами типа REAL.
Блочный элемент математической функции имеет вход IN и выход OUT, а также вход разрешения EN и выход разрешения ENO. Заголовок в блочном элементе идентифицирует выполняемую математическую функцию.
Пример обозначения блочного элемента математической функции синус приведен на рисунке 2.25.
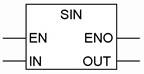
Рисунок 2.25 - Обозначение блочного элемента "синус"
Входное значение подается на вход IN, а результат математической функции выводится на выход OUT. Вход и выход относятся к типу данных REAL. Операнды, которые адресуются с использованием абсолютных адресов, должны иметь размер двойного слова.
Математическая функция выполняется, если на входе разрешения (EN) присутствует сигнал «1». Если при вычислении возникнет ошибка, то выход разрешения ENO устанавливается в «0». Если выполнение функции не разрешено (EN = 0), то вычисление не выполняется и ENO также становится равным «0».
Если главное реле управления (MCR) активно, то при выполнении математической функции (EN = 1) выход OUT устанавливается в нуль. При этом MCR не влияет на ENO.
В математической функции могут возникнуть следующие ошибки:
• выход за границы диапазона и переполнение;
• недопустимое число типа REAL как входное значение.
Пример
Вычисление функции синус показано на рисунке 2.26. Значение двойного слова памяти (меркеров) MD 110 содержит величину в радианах. От этого значения берется синус и сохраняется в двойном слове памяти MD 104.
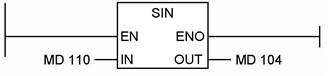
Рисунок 2.26 - Пример вычисления функции синус
Дата добавления: 2016-12-09; просмотров: 3394;











