Некоторые плоские кривые линии

Эллипс, парабола, гипербола - алгебраические кривые второго порядка определяются уравнением f (х ,у) = 0.

Эллипс

АВ = 2а - большая ось эллипса

CD = 2в - малая ось эллипса

О - центр эллипса

F₁; F₂ - фокусы эллипса

А,В,С,D - вершины эллипса

Точки M и N - любые точки эллипса

|MF₁| + |MF₂| = |NF₁| + |NF₂| = АВ - Const

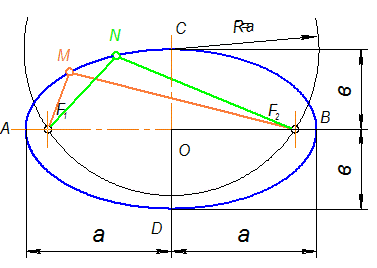
Рис. 1-53

Эллипс - это все множество точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная, равная 2а.

У эллипса все точки собственные. Кривая симметрична относительно обеих осей. Всегда можно подобрать такую пару диаметров эллипса, что: хорды, параллельные одному диаметру, делятся другим диаметром пополам, такие диаметры называются сопряженными.

Графически можно построить любую точку эллипса, если заданы его оси. Эллипс на рис. 1-54 построен равномерным сжатием окружности в направлении ОС ^ ОА

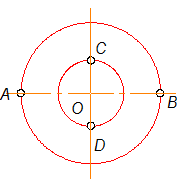
АВ - большая ось

СD - малая ось

Разделить окружности на 12 равных частей

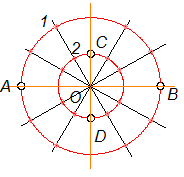
Из точек пересечения любого луча с окружностями провести прямые, параллельные осям эллипса:

из точки 1 || СD, из точки 2 || АВ.

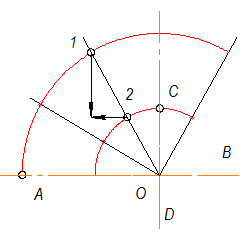
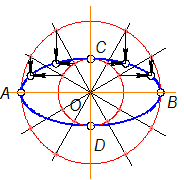
Рис. 1-54

Парабола

Парабола обладает одной осью и имеет две вершины: О - собственная точка и S ¥ - несобственная точка (парабола имеет одну несобственную точку), F - фокус и Р - параметр параболы

Парабола - это все множество точек, равноудаленных от прямой d (директрисы) и данной точки F (фокуса)

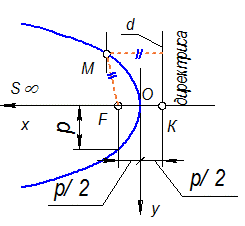
Рис. 1-55

Если требуется построить параболу по заданной вершине О, оси Х и точки М, то строится прямоугольный треугольник - ОАМ (рис. 1-56)

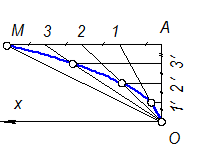
Рис. 1-56

Гипербола

Гипербола - разомкнутая кривая, состоящая из двух симметричных ветвей; она имеет две оси симметрии - действительную (ось - х) и мнимую (ось - у). Асимптоты - это прямые, к которым ветви гиперболы неограниченно приближаются при удалении в бесконечность (рис. 1-57).

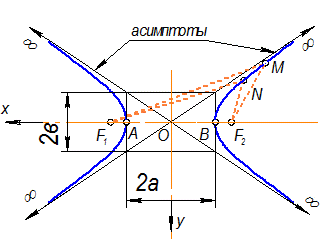
Рис. 1-57

Точки А и В - вершины гиперболы.

F₁ и F₂ - фокусы гиперболы

|MF₁| - |MF| = |NF₁| - |NF₂| = const = 2a

Расстояние между F₁ и F₂ равняется сумме (а² + в²)

Гипербола - это все множество точек, разность расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная, равная 2а.

Построение гиперболы, если заданы вершины А и В и фокусы F₁ и F₂.

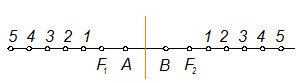
Рис. 1-58

Точки - 1, 2, 3, 4, 5 - ряд произвольно взятых точек. Из фокусов F₁ и F₂, как из центров, проводят дуги, радиусами которых служат расстояния от вершин А и В до точек 1, 2, 3, 4, 5 и т.д.. (рис. 1-59) R₂ = В1, В2, В3, В4, В5 R = А1, А2, А3, А4, А5

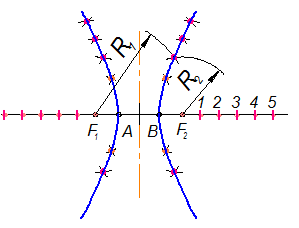
Рис. 1-59

Эвольвента

Эвольвента (развертка окружности)- эта лекальная кривая широко применяется в технике. Например, форма боковой поверхности зуба зубчатых передач, называемая профилем зуба, очерчивается по эвольвенте.

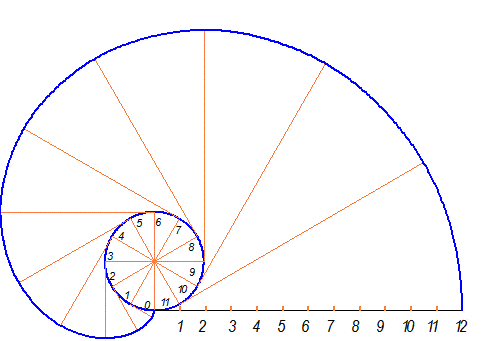
Рис. 1-60