Квантово-механическая модель атома водорода

В 1924 г. французский физик Луи де Бройль предположил, что электрон одновременно обладает и волновыми и корпускулярными свойствами. Сопоставляя уравнение Планка Е = hn и уравнение Эйнштейна Е = mc² Луи де Бройль получил простую зависимость, в которой между собой связаны как корпускулярные (Е, m, u), так и волновые (l, n) свойства:

mc² = hn, l = h/mc

Согласно де Бройлю, движущейся частице с массой mи скоростью u соответствует длина волны

,

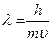где l - длина волны движущейся частицы.

Волны частиц материи де Бройль назвал материальными волнами. Они свойственны всем частицам или телам, но как следует из уравнения де Бройля, длина волны для макротела ничтожно мала, что не поддается экспериментальному измерению. Например, для тела массой 1000 кг, двигающегося со скоростью 30 м/с λ = 2,21∙10^-38м.

Однако для микрочастиц, например электрона, волновой характер движения был экспериментально подтвержден в 1927 г. Дэвиссоном и Джермером, обнаружившими дифракцию электронов, подобную дифракции света.

Согласно уравнению де Бройля, с движением электрона (масса 9,1∙10^{-28 г}) ассоциируется волна длиной:

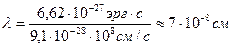
т.е. ее длина соизмерима с размером атомов. Поэтому при рассеянии электронов кристаллами наблюдается дифракция, причем кристаллы проявляют свойства дифракционной решетки.

Для микрочастиц справедливы законы квантовой механики, основу которой составили работы Луи де Бройля, Шредингера и Гейзенберга.

Принцип неопределенности. Кажущуюся двойственную природу микрочастиц объясняет установленной Вернером Гейзенбергом в 1927 г. принцип неопределенности: невозможно одновременно определить и скорость (или импульс p = mu) и положение микрочастицы (ее координаты). Математическое выражение принципа неопределенности имеет вид:

где D x – неопределенность положения электрона в пространстве; D u- неопределенность количества движения; h – постоянная Планка; m – масса электрона.

Произведение неопределенностей положения (D x) и скорости (D u) никогда не может быть меньше h/m, из этого соотношения следует, что чем точнее определены координаты частицы (чем меньше неопределенность D x), тем менее определенной становится величина ее скорости (больше D u) и наоборот. Так, если положение электрона определено с точностью до 10^-10см, то неопределенность в скорости составит 58000 км/с (при скорости электрона 2000 км/с). Двойственная природа электрона – корпускулярная и волновая – не совместима с понятиями классической механики, которая представляет электрон, как точечную частицу, описывающую вполне определенную траекторию со скоростью, известной в каждый момент времени.

Квантовая механика заменяет классическое понятие точного местонахождения частицы понятием статистической вероятности нахожденияэлектрона в данной точке пространства, или в элементе объема атома dV.

Волновое уравнение Шредингера.Вычисление вероятности нахождения электрона в данной точке и его энергия – сложная математическая проблема. В 1926 г. Эрвин Шредингер предложил уравнение, получившего название волнового

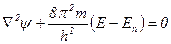
уравнения Шредингера, которое в квантовой механике имеет такое же значение, какое имеют законы Ньютона в классической механике. В этом уравнении в качестве параметров используются масса и потенциальная энергия электрона, а разрешается оно относительно волновой функции ψ,описывающей волновой характер движения электрона, где E, E_n – соответственно полная и потенциальная энергии электрона; m – масса движущегося электрона, Ñ (‘‘набла’’) – оператор Ла Пласса, показывающий, какое действие надо произвести; Ñ ²y = ¶ ²y /¶ x ² + ¶ ²y /¶ y² + ¶ ²y /¶ z ² – сумма вторых производных волновой функции yпо координатам x, y, z; m – масса электрона; h – постоянная Планка.

Различным функциям ψ₁ , ψ_{2 ,} ψ₃ ,…, ψ_n.,которыеявляются решением волнового уравнения, каждой соответствует свое значение энергии Е₁ , Е₂ , Е₃ ,…, Е_n

Уравнение Шредингера имеет бесконечное множество решений. Для того чтобы его решения имели смысл, т.е. чтобы оно описывало поведение электрона в атоме, должны удовлетворяться следующие требования: функция ψдолжна быть однозначной, непрерывной и конечной, а также нормированной. Эти условия, налагаемые на функцию ψ, эквивалентны квантовым условиям, сформулированным впервые Бором в виде постулатов.

Волновая функция.Волновая функция ψ при решении уравнения Шредингера может принимать различные значения, в частности быть величиной мнимой и отрицательной, но вероятность нахождения электрона в данном элементарном объеме атома должна быть величиной действительно положительной. Поэтому все наблюдаемые свойства электрона выражают через произведение yy* = |y| ², где y* - комплексносопряженная волновая функция. Борн предложил рассматривать квадрат модуля y - функции |y| ² как плотность вероятности обнаружения электрона в тех или иных точках объема. Если умножить |y| ² на элементарный объем dV, взятый в точке с координатами x,yи z: dV = dx×dy×dz, то получим |y| ²dV – вероятность того, что электрон будет обнаружен в пределах элементарного объема dV. Вероятность же нахождения электрона в объеме атома должна быть равна единице: ò|y| ² dV = 1. Та часть пространства атома, где плотность вероятности |y| ² велика, и будет местом наиболее вероятного пребывания электрона.

В качестве модели состояния электрона в атоме в квантовой механике принято представление об электронном облаке,

плотность соответствующих участков которого пропорциональна вероятности нахождения там электрона. Одна из возможных форм электронного облака в атоме показана на рис. 2.

Рис. 2. Одна из возможных форм электронного облака

Этот рисунок можно интерпретировать следующим образом. Допустим, что в какой-то момент времени удалось сфотографировать положение электрона в трехмерном пространстве вокруг ядра и на фотографии это отразится в виде точки. Если повторить такое определение тысячи раз, то новые фотографии, сделанные через малые промежутки времени обнаружат электрон в новых положениях. При наложении множества таких фотографий образуется картина, напоминающая облако. Очевидно, облако окажется наиболее плотным там, где наибольшее число точек, т.е. в областях наиболее вероятного нахождения электрона. Электронное облако часто изображают в виде граничной поверхности рис. 3 (охватывающий примерно 90 % электронного облака). При этом обозначение электронной плотности с помощью точек опускают.

Рис. 3. Электронное облако в виде граничной поверхности

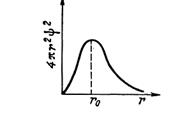Рис. 4. Радиальное распределение вероятности

для 1s - электрона

Электронное облако изображают также с помощью кривой радиального распределения вероятности (рис.4). Эта кри

вая показывает вероятность того, что электрон находится в тонком концентрическом шаровом слое радиуса r и толщины dr вокруг ядра. Объем этого слоя равен dV = 4πr²dr. Общая вероятность нахождения электрона в этом слое (4πr²)ψ².

Так как масса протона много больше массы электрона, то протон считают центром тяжести системы p⁺ –или началом координат. Уравнение Шредингера, содержащее сферические координаты r, U и j в качестве переменных величин, определяющих положение электрона, можно уже представить в виде произведения трех функций, каждая из которых содержит только одну переменную:

y (r, U,j) = R(r)×U(q)×F(j)

Функцию R(r) называют радиальной частью волновой функции, а U(q) и F(j) – её угловой частью (U и F - заглавные буквы “тэта” и “фи” греческого алфавита).

Подставляя это выражение волновой функции в уравнение Шредингера, определяют его через новые переменные, уравнения, каждое из которых содержит только одну переменную координату: y_n,l(r), y_{l, ml} (r), y _ml(j). Из решения этих уравнений находят целочисленные параметры n, l, m_l, получившие названия квантовых чисел. Таким образом, появление квантовых чисел автоматически вытекает из решения уравнения Шредингера для атома водорода.

Квантовые числа

Волновая функция, являющаяся решением уравнения Шредингера, называется орбиталью. Для решения этого уравнения вводятся три квантовых числа (n, l и m_l)

Главное квантовое число n. оно определяет энергию электрона и размеры электронных облаков. Энергия электрона главным образом зависит от расстояния электрона от ядра: чем ближе к ядру находится электрон, тем меньше его энергия. Поэтому можно сказать, что главное квантовое число n определя-

ет расположение электрона на том или ином энергетическом уровне. Главное квантовое число имеет значения ряда целых чисел от 1 до ∞. При значении главного квантового числа, равного 1 (n = 1), электрон находится на первом энергетическом уровне, расположенном на минимально возможном расстоянии от ядра. Общая энергия такого электрона наименьшая.

Электрон, находящийся на наиболее удаленном от ядра энергетическом уровне, обладает максимальной энергий. Поэтому при переходе электрона с более удаленного энергетического уровня на более близкий выделяется энергия. Энергетические уровни обозначают прописными буквами согласно схеме:

Значение n …. 1 2 3 4 5

Обозначение K L M N Q

Орбитальное квантовое число l.Согласно квантово-механическим расчетам электронные облака отличаются не только размерами, но и формой. Форму электронного облака характеризует орбитальное или побочное квантовое число. Различная форма электронных облаков обусловливает изменение энергии электрона в пределах одного энергетического уровня, т.е. ее расщепления на энергетические подуровни. Каждой форме электронного облака соответствует определенное значение механического момента движения электрона m, определяемого орбитальным квантовым числом:

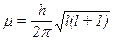
Определенной форме электронного облака соответствует вполне определенное значение орбитального момента количества движения электрона m. Так как m может принимать только дискретные значения, задаваемые квантовым числом l, то и формы электронных облаков не могут быть произвольными: каждому возможному значению l соответствует вполне определенная форма электронного облака.

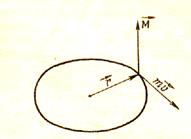Рис. 5. Графическая интерпретация момента движения электрона, где μ - орбитальный момент количества

движения электрона

Орбитальное квантовое число может иметь значения от 0 до n - 1, всего n – значений.

Энергетические подуровни обозначены буквами:

Значение l 0 1 2 3 4

Обозначение s p d f g

Магнитное квантовое число m_l. Из решения уравнения Шредингера следует, что электронные облака ориентированы определенным образом в пространстве. Пространственная ориентация электронных облаков характеризуется магнитным квантовым числом.

Магнитное квантовое число может принимать любые целочисленные значения как положительные, так и отрицательные в пределах от –l до +l, а всего это число может принимать (2l+1) значений для данного l, включая нулевое. Например, если l = 1, то возможны три значения m (–1,0,+1) орбитальный момент m, есть вектор, величина которого квантована и определяется значением l. Из уравнения Шредингера следует, что не только величина µ, но и направление этого вектора, характеризующее пространственную ориентацию электронного облака, квантовано. Каждому направлению вектора заданной

длины соответствует определенное значение его проекции на ось z, характеризующее некоторое направление внешнего магнитного поля. Значение этой проекции характеризует m_l.

Спин электрона.Изучение атомных спектров показало, что три квантовых числа n, l и m_l не являются полной характеристикой поведения электронов в атомах. С развитием спектральных методов исследований и повышением разрешающей способности спектральных приборов была обнаружена тонкая структура спектров. Оказалось, что линии спектров расщепляются. Для объяснения этого явления было введено четвертое квантовое число, связанное с поведением самого электрона. Это квантовое число было названо спином с обозначением m_s и принимающее всего два значения +½ и –½ в зависимости от одной из двух возможных ориентаций спина электрона в магнитном поле. Положительное и отрицательное значения спина связаны с его направлением. Поскольку спин величина векторная, то его условно обозначают стрелкой, направленной вверх или ↑ или вниз ↓ .Электроны, имеющие одинаковое направление спина называются параллельными, при противоположных значениях спинов – антипараллельныи.

Наличие спина у электрона было доказано экспериментально в 1921 г., В. Герлахом и О. Штерном, которые сумели разделить пучок атомов водорода на две части, соответствующие ориентации электронного спина. Схема их эксперимента показана на рис. 6. Когда атомы водорода пролетают через область сильного магнитного поля, электрон каждого атома взаимодействует с магнитным полем, и это заставляет атом отклоняться от исходной прямолинейной траектории, Направление, в котором отклоняется атом, зависит от ориентации спина его электрона. Спин у электрона не зависит от внешних условий и не может быть уничтожен или изменен.

Таким образом, было окончательно установлено, что полностью состояние электрона в атоме характеризуется четырьмя квантовыми числами n, l, m_l. и m_s,

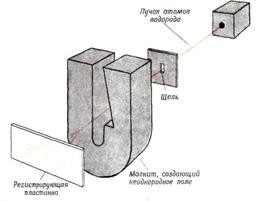
Рис. 6. Схема эксперимента Штерна - Герлаха

Атомные орбитали

Совокупность положений электрона в атоме, характеризуемых определенными значениями квантовых чисел n, l и m_l называются атомной орбиталью (АО).

Таким образом, атомная орбиталь – геометрический образ одноэлектронной волновой функции y, зависящей от трех квантовых чисел n, l и m_l, представляющей собой область наиболее вероятного пребывания электрона в атоме.

Атомные орбитали принято обозначать при помощи двух квантовых чисел n и l. Например, 3s – AO (n = 3, l = 0); 4d – AO (n = 4, l = 2); 3p – AO (n = 3, l = 1). Форма и размеры АО зависят от квантовых чисел n, l и m_l и, следовательно, изменяются от одного электрона в атоме к другому его состоянию. Главное квантовое число n определяет размеры АО; чем больше значение n, тем больше область наиболее вероятного пребывания электрона около ядра атома. Например, 2s – AO > 1s – AO, 5p – AO > 4p – AO.

Орбитальное квантовое число l определяет конфигурацию АО, которая от значения n не зависит. При l = 0 (при всех значениях n) AO будет иметь сферическую форму, при l = 1 – форму гантели, при l = 2 – более сложную пространственную форму (рис.7).

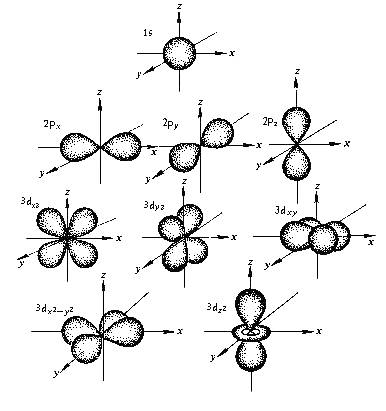Рис. 7. Формы и ориентация в пространстве электронных

облаков 1s-, 2p- и 3d- орбиталей

Магнитное квантовое число m_l связано с ориентацией АО в пространстве. Если ns – AO (l = 2, m_l = 0) сферически симметрично, то p – и d – AO имеют характерную направленность в трехмерном пространстве (рис. 7).

Условно АО изображают в виде квадрата, называемый квантовой или электронной ячейкой . Так как каждой АО отвечает только одно значение магнитного квантового числа m_е, то число АО или квантовых ячеек для данной величины орбитального квантового числа будет следующим:

np – AO , для которых m_l = -1,0,+1

^(n³2)

nd – AO , для которых m_l =

^(n³3) -2, -1, 0, +1, +2

nf – AO , для которых m_l =

^(n³4) -3, -2, 0, +1, +2, +3