Атом водорода в квантовой механике
Уравнение Шредингера для атома водорода
Самой простой задачей квантовой механики является задача о движении электрона в кулоновском поле ядра. Это задача об атоме водорода и водорода подобных ионов: однократно ионизированный гелий и однократно ионизированный литий.
Потенциальная энергия взаимодействия электрона с ядром:
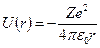 , ,
| (1) |
где 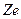 - заряд ядра (для атома водорода
- заряд ядра (для атома водорода 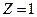 ),
), 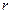 - расстояние между электроном и ядром.
- расстояние между электроном и ядром.
Графически функция 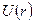 изображена на рис.1. С уменьшением
изображена на рис.1. С уменьшением 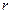 функция
функция 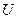 убывает (возрастает по модулю).
убывает (возрастает по модулю).
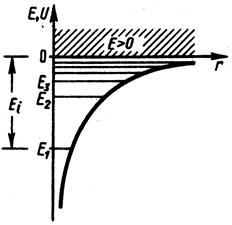 Рис.1.
Рис.1.
|
Состояние электрон в атоме водорода описывается волновой функцией 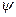 , удовлетворяющей стационарному уравнению Шредингера, учитывающему выражение (1):
, удовлетворяющей стационарному уравнению Шредингера, учитывающему выражение (1):
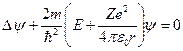 , ,
| (2) |
где 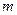 - масса электрона, а
- масса электрона, а 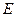 - полная энергия электрона в атоме.
- полная энергия электрона в атоме.
Уравнение (2) имеет решения, удовлетворяющие требования однозначности, конечности и непрерывности волновой функции только при следующих собственных значениях энергии:
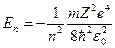 , ( , ( 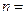 1, 2, 3,…). 1, 2, 3,…).
| (3) |
Таким образом, из решения уравнения Шредингера следует, что энергия электрона в атоме квантуется. Формула (3) дает набор дискретных значений энергии, совпадающими со значениями энергии, найденными из спектров. Возможные значения показаны на рис.1. в виде горизонтальных прямых. Самый низкий уровень энергии 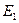 называется основным, все остальные – возбужденными. При
называется основным, все остальные – возбужденными. При 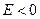 движение электрона является связанным: по мере роста главного квантового числа энергетические уровни располагаются теснее и при
движение электрона является связанным: по мере роста главного квантового числа энергетические уровни располагаются теснее и при 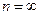
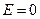 . При
. При 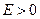 движение электрона является свободным. Область непрерывного спектра
движение электрона является свободным. Область непрерывного спектра 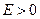 соответствует ионизированному атому. Энергия ионизации атома водорода равна:
соответствует ионизированному атому. Энергия ионизации атома водорода равна:
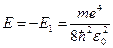 = 13,55 эВ = 13,55 эВ
|
Квантовые числа.
Собственные функции 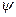 , являющиеся решениями уравнения Шредингера зависят от трех квантовых чисел:
, являющиеся решениями уравнения Шредингера зависят от трех квантовых чисел: 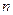 ,
, 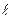 и
и 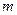 .
. 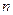 - главное квантовое число, определяет энергетические уровни электрона в атоме и принимает значения
- главное квантовое число, определяет энергетические уровни электрона в атоме и принимает значения 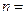 1, 2, 3,…
1, 2, 3,…
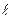 - орбитальное квантовое число, оно связано с квантованием момента импульса электрона (механического орбитального момента). То есть орбитальный момент не может быть произвольным, а принимает дискретные значения, определяемые формулой:
- орбитальное квантовое число, оно связано с квантованием момента импульса электрона (механического орбитального момента). То есть орбитальный момент не может быть произвольным, а принимает дискретные значения, определяемые формулой:
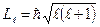
| (4) |
При данном значении 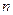
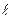 - принимает значения
- принимает значения
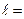 0,1, 2,…, 0,1, 2,…, 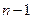 . .
|
Всего 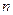 значений.
значений.
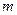 - магнитное квантовое число, связанное с квантованием проекции момента импульса на выбранное направление (обычно в направлении магнитного поля по оси
- магнитное квантовое число, связанное с квантованием проекции момента импульса на выбранное направление (обычно в направлении магнитного поля по оси 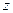 ):
):
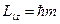
| (5) |
Магнитное квантовое число может принимать следующие значения:
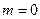 , , 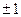 , , 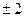 ,…, ,…, 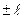
|
Всего 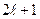 значений.
значений.
Таким образом, вектор момента импульса электрона может иметь такие ориентации в пространстве, при которых его проекция на выделенное направление (ось 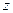 ) принимает квантованные значения согласно формуле (5). Это означает, что в магнитном поле уровень с орбитальным квантовым числом
) принимает квантованные значения согласно формуле (5). Это означает, что в магнитном поле уровень с орбитальным квантовым числом 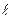 расщепляется на
расщепляется на 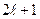 подуровней. Это было в 1896 году экспериментально обнаружено голландским физиком Зееманом.
подуровней. Это было в 1896 году экспериментально обнаружено голландским физиком Зееманом.
Из формулы (3) следует, что каждому значению 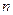 соответствует энергия
соответствует энергия 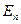 . Каждой энергии
. Каждой энергии 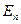 соответствует несколько волновых функций
соответствует несколько волновых функций 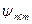 отличающихся значениями
отличающихся значениями 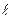 и
и 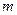 . То есть при одном и том же значении энергии атом водорода может быть в нескольких различных состояниях. Найдем число состояний с одинаковой энергией
. То есть при одном и том же значении энергии атом водорода может быть в нескольких различных состояниях. Найдем число состояний с одинаковой энергией 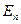 . Так как при данном
. Так как при данном 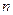 орбитальное квантовое число
орбитальное квантовое число 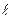 изменяется от
изменяется от 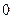 до
до 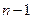 , а каждому
, а каждому 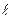 соответствует
соответствует 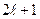 значений
значений 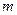 , то число различных состояний равно:
, то число различных состояний равно:
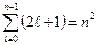
| (6) |
В квантовой механике состояния с различными 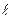 обозначают буквенными символами как и спектроскопии:
обозначают буквенными символами как и спектроскопии:
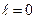 - s-состояние
- s-состояние
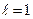 - p-состояние
- p-состояние
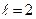 - d-состояние
- d-состояние
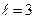 - f-состояние
- f-состояние
При записи квантового состояния сначала пишут численное значение 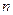 , а затем буквенное
, а затем буквенное 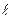 . Например, состояние
. Например, состояние 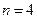 и
и 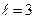 обозначают
обозначают 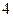 f.
f.
Квадрат модуля волновой функции 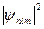 определяет вероятность обнаружения электрона в единице объема. Электрон при своем движении как бы «размазан», образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках атома.
определяет вероятность обнаружения электрона в единице объема. Электрон при своем движении как бы «размазан», образуя электронное облако, плотность которого характеризует вероятность нахождения электрона в различных точках атома.
Квантовые числа 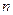 и
и 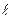 характеризуют размер и форму электронного облака, а квантовое число
характеризуют размер и форму электронного облака, а квантовое число 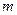 - его ориентацию в пространстве. На рис.2. для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при
- его ориентацию в пространстве. На рис.2. для примера приведено распределение электронной плотности (формы электронного облака) для состояний атома водорода при 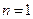 и
и 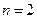 . Как видно из рисунка, оно зависит от
. Как видно из рисунка, оно зависит от 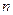 ,
, 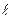 и
и 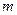 . При
. При 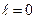 электронное облако имеет форму шара, при
электронное облако имеет форму шара, при 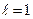 - форму гантели.
- форму гантели.
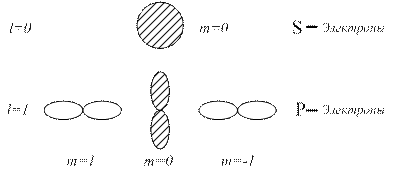 Рис.2.
Рис.2.
|
Радиус шара в 1s состоянии равен радиусу первой орбиты Бора. По теории Бора электрон может находиться только на орбите, в квантовой механике – в любом месте пространства, но с разной плотностью.
Спин электрона.
При изучении спектра атома водорода обнаружили, что они имеют дуплетную структуру (каждая спектральная линия расщеплена на две полоски). Чтобы объяснить это явление предположили, что электрон обладает собственным механическим моментом импульса – спином ( 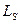 ). Первоначально спин связывали с вращением электрона вокруг своей оси. Впоследствии выяснилось, что это ошибочно. Спин – это внутреннее квантовое свойство электрона – у него нет классического аналога. Спин квантуется по закону:
). Первоначально спин связывали с вращением электрона вокруг своей оси. Впоследствии выяснилось, что это ошибочно. Спин – это внутреннее квантовое свойство электрона – у него нет классического аналога. Спин квантуется по закону:
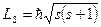 , ,
|
где 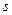 - спиновое квантовое число.
- спиновое квантовое число.
По аналогии с орбитальным моментом импульса, проекция 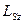 спина квантуется так, что вектор
спина квантуется так, что вектор 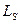 может принимать
может принимать 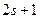 ориентаций. Так как спектральная линия расщепляется только на две части, то ориентаций
ориентаций. Так как спектральная линия расщепляется только на две части, то ориентаций 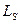 только две:
только две: 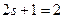 , отсюда
, отсюда 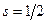 . Проекция спина на выделенное направление определяется выражением:
. Проекция спина на выделенное направление определяется выражением:
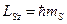 , ,
|
где 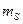 - магнитное квантовое число. Оно может иметь только два значения
- магнитное квантовое число. Оно может иметь только два значения 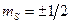 .
.
Таким образом, опытные данные привели к необходимости введения спина. Поэтому для полного описания состояния электрона в атоме необходимо наряду с главным, орбитальным и магнитным квантовыми числами задавать еще магнитное спиновое квантовое число.
Принцип Паули. Распределение электронов в атоме по состояниям.
Состояние каждого электрона в атоме характеризуется четырьмя квантовыми числами:
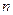 (
( 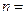 1, 2, 3,…) – квантует энергию
1, 2, 3,…) – квантует энергию 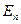 ,
,
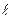 (
( 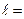 0, 1, 2,…,
0, 1, 2,…, 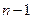 ) – квантует орбитальный механический момент
) – квантует орбитальный механический момент 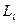 ,
,
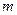 (
( 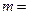 0,
0, 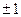 ,
, 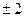 ,…,
,…, 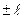 ) – квантует проекцию момента импульса на заданное направление
) – квантует проекцию момента импульса на заданное направление 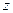
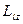 ,
,
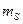 (
( 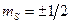 ) – квантует проекцию спина на заданное направление
) – квантует проекцию спина на заданное направление 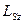 .
.
С возрастанием 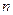 растет энергия. В нормальном состоянии атома электроны находятся на самых низких энергетических уровнях. Казалось бы, что все они должны быть в состоянии 1s. Но опыт показывает, что это не так.
растет энергия. В нормальном состоянии атома электроны находятся на самых низких энергетических уровнях. Казалось бы, что все они должны быть в состоянии 1s. Но опыт показывает, что это не так.
Швейцарский физик В.Паули сформулировал принцип: в одном и том же атоме не может быть двух электронов с одинаковыми квантовыми числами 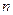 ,
, 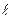 ,
, 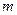 ,
, 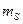 . То есть два электрона должны отличаться по крайней мере значениями одного квантового числа.
. То есть два электрона должны отличаться по крайней мере значениями одного квантового числа.
Значению 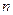 соответствует
соответствует 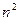 состояний, отличающихся значениями
состояний, отличающихся значениями 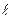 и
и 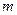 . Но еще
. Но еще 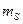 имеет два значения
имеет два значения 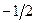 и
и 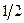 , значит всего
, значит всего 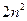 состояний. Поэтому в состояниях с заданным
состояний. Поэтому в состояниях с заданным 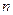 находиться
находиться 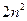 электронов. Совокупность электронов с одинаковым
электронов. Совокупность электронов с одинаковым 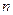 называется слоем, а с одинаковыми
называется слоем, а с одинаковыми 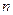 и
и 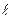 - оболочкой.
- оболочкой.
Поскольку орбитальное квантовое число 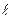 принимает значения от
принимает значения от 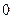 до
до 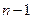 , число оболочек в слое равно
, число оболочек в слое равно 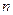 . Количество электронов в оболочке определяется магнитным и спиновым квантовыми числами: максимальное число электронов в оболочке с заданным
. Количество электронов в оболочке определяется магнитным и спиновым квантовыми числами: максимальное число электронов в оболочке с заданным 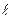 равно
равно 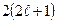 . Обозначение слоев и распределение электронов по слоям и оболочкам представлены в таблице 1.
. Обозначение слоев и распределение электронов по слоям и оболочкам представлены в таблице 1.
| Символ слоя | Максимальное число электронов в оболочках
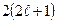
| Макс. число электронов в слое 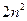
| ||||
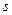 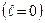
| 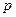 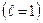
| 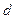 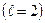
| 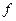 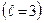
| 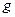 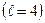
| |||
| K | |||||||
| L | |||||||
| M | |||||||
| N | |||||||
| O |
Пользуясь распределением электронов по состояниям можно объяснить периодический закон Менделеева. Каждый последующий атом имеет на один электрон больше, располагается он в состоянии с возможно меньшей энергией.
Периодическая система элементов начинается с простейшего атома водорода. Его единственный электрон находится в состоянии 1s, характеризуемом квантовыми числами 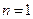 ,
, 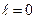 и
и 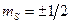 (ориентация спина произвольна).
(ориентация спина произвольна).
В атоме 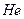 два электрона находятся в 1s состоянии с антипараллельными спинами. На атоме
два электрона находятся в 1s состоянии с антипараллельными спинами. На атоме 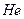 заканчивается заполнение K-слоя, что соответствует завершению 1 периода Периодической системы Менделеева.
заканчивается заполнение K-слоя, что соответствует завершению 1 периода Периодической системы Менделеева.
У атома 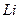 3 электрона. Согласно принципу Паули третий электрон уже не может разместиться в целиком заполненном слое К и занимает наинизшее энергетическое состояние с
3 электрона. Согласно принципу Паули третий электрон уже не может разместиться в целиком заполненном слое К и занимает наинизшее энергетическое состояние с 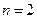 (L-слой), то есть 2s состояние. Электронная конфигурация для атома
(L-слой), то есть 2s состояние. Электронная конфигурация для атома 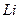 : 1
: 1 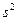 2
2 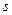 . Атомом
. Атомом 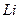 начинается 2 период Периодической системы Менделеева. Заканчивается 2 период инертным газом неоном. У атома неона полностью заполнена 2p оболочка и полностью заполнен слой L.
начинается 2 период Периодической системы Менделеева. Заканчивается 2 период инертным газом неоном. У атома неона полностью заполнена 2p оболочка и полностью заполнен слой L.
Одиннадцатый электрон 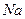 размещается в M слое (
размещается в M слое ( 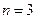 ), занимая наименьшее состояние 3s. Электронная конфигурация для
), занимая наименьшее состояние 3s. Электронная конфигурация для 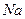 : 1
: 1 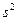 2
2 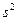 2
2 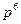 3
3 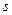 . Электрон 3s (как и 2s у лития) является валентным, поэтому свойства
. Электрон 3s (как и 2s у лития) является валентным, поэтому свойства 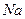 подобны свойствам
подобны свойствам 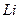 .
. 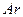 завершает 3 период. Его электронная конфигурация
завершает 3 период. Его электронная конфигурация 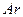 : 1
: 1 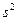 2
2 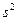 2
2 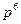 3
3 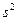 3
3 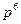 . Начиная с атома калия в застройке электронных оболочек происходит отклонение. Вместо заполнения 3d оболочки, заполняется сначала 4s (
. Начиная с атома калия в застройке электронных оболочек происходит отклонение. Вместо заполнения 3d оболочки, заполняется сначала 4s ( 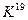 : 1
: 1 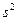 2
2 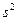 2
2 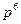 3
3 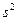 3
3 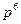 4
4 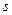 ). Это происходит потому, что оболочка 4s энергетически выгоднее, ближе расположена к ядру, чем 3d. После заполнения 4s заполняется 3d, а затем 4р оболочка, которая дальше от ядра, чем 3d.
). Это происходит потому, что оболочка 4s энергетически выгоднее, ближе расположена к ядру, чем 3d. После заполнения 4s заполняется 3d, а затем 4р оболочка, которая дальше от ядра, чем 3d.
С такими отклонениями приходится сталкиваться и дальше. Оболочка 4f, которая содержит 14 электронов, начинает заполняться после того, как заполняются 5s, 5p, 6s. В итоге у элементов 58-71 добавляющиеся электроны садятся в 4f состояния, а внешние электронные оболочки у этих элементов одинаковы. Поэтому их свойства близки. Эти элементы называют лантанидами. Аналогично близки по свойствам актиниды (90-103), где заполняется 5f оболочка при неизменном 7 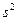 .
.
Таким образом, открытая Менделеевым периодичность в химических свойствах элементов объясняется повторяемостью в структуре внешних оболочек у атомов родственных элементов.
Валентность химического элемента равна числу электронов в s или р оболочке с максимальным n. Если s, p, d,… оболочки полностью заполнены, то их спины скомпенсированы. Такие элементы являются диамагнетиками. Если оболочки не полностью заполнены, то имеются не скомпенсированные спины. Это парамагнетики.
| <== предыдущая лекция | | | следующая лекция ==> |
| Элементы квантовой механики | | | Оптические квантовые генераторы |
Дата добавления: 2016-05-28; просмотров: 6589;











