Адиабатный процесс.

Адиабатным называется процесс, протекающий без теплообмена с внешней средой: dQ=0, Q=0

Чтобы процесс был адиабатным, необходимо, чтобы система была отделена от окружающих тел теплонепроницаемой перегородкой, либо процесс должен быть очень быстро протекающим, причем настолько быстро, чтобы не успел установиться теплообмен.

Из первого закона термодинамики: dA=-dU, то естьработа при адиабатическом процессе совершается за счет убыли внутренней энергии.

Для получения уравнений адиабатного процесса рассмотрим один моль газа, для которого:

dA=pdV, dU=C_VdT

следовательно,

pdV =C_VdT

Из уравнения Менделеева-Клапейрона для 1 моля газа

p=RT/V

тогда

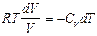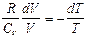, или . (8.5.1)

Из уравнения Майера: R=C_p – C_V, тогда

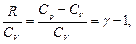
где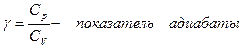

Следовательно, уравнение (8.5.1) примет вид

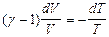
Пусть произошел адиабатный процесс из состояния с параметрами (V₁,T₁) в состояние с (V₂,T₂).

Проведем интегрирование с соответствующими пределами:

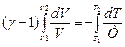, Þ ,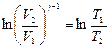

.

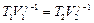Для адиабатного процесса уравнение состояния:

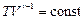(8.5.2)

Из уравнения Менделеева-Клапейрона: T=pV/R.

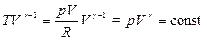; т.е. 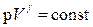(8.5.3)

Из уравнения Менделеева-Клапейрона: V=RT/p.

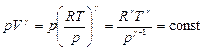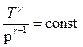; (8.5.4)

Уравнения (8.5.2), (8.5.3) и (8.5.4) – уравнения адиабатного процесса, названы уравнениями Пуассона.

Работа адиабатического расширения:

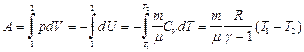
Здесь мы учли полученное нами из уравнения Майера соотношение: 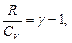откуда . Итак, работа по расширению при адиабатном процессе: .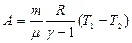

При сопоставлении адиабатного и изотермического процессов (рис. 8.4) видно, что адиабата проходит более круто, чем изотерма: для изотермы – pV=const, для адиабаты 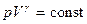, а показатель адиабаты g>1, то есть давление при адиабатическом процессе зависит сильнее.

Объясним этот факт с молекулярно-кинетической точи зрения. давление газа обусловлено ударами молекул о стенки сосуда. При изотермическом процессе изменяется число ударов молекул в единицу времени на единицу площади, а средняя сила ударов не изменяется. При адиабатном процессе изменяются, и среднее число ударов в единицу времени, и средняя сила ударов.

Политропным называется термодинамический процесс, в котором теплоемкость тела постоянна: С=const. Уравнения политропного процесса в идеальном газе:

pVⁿ=const, ТV^n-1=const,

где 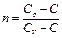– показатель политропы.