Недостижимость абсолютного нуля.

Второе начало термодинамики можно использовать для построения термодинамической шкалы температур. Так как КПД цикла Карно не зависит от рабочего тела, то для измерения температуры можно использовать обратимый цикл Карно. Некоторое стандартное тело в определенном состоянии (например, вода, кипящая при атмосферном давлении) выбирается в качестве нагревателя. Другое стандартное тело (например, лед. тающий при атмосферном давлении) выбирается в качестве холодильника. Разность температур Т_н и Т_х (сами температуры пока неизвестны) делится на произвольное число частей и устанавливается значение градуса (скажем, на сто частей). Осуществляется идеальный цикл Карно с каким-либо веществом. Измеряется количество теплоты Q₁, заимствованной от нагревателя, и количество теплоты Q₂, отданной холодильнику.

Согласно выражению для КПД тепловой машины:

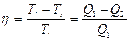
откуда

.

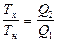Учитывая, кроме того, условие разности температур Т_н–Т_х=100^о, получаем два уравнения, определяющие температуры Т_н и Т_х. Если теперь взять некоторое вещество при неизвестной температуре Т и использовать его в качестве нагревателя при прежнем холодильнике (температура Т_х), то, проводя цикл Карно и измеряя Q₁^/ и Q₂^/, можно написать: 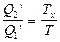. Отсюда находится искомая температура. Построенная таким образом шкала температур, как выяснилось, практически совпадает со шкалой, получаемой при измерениях с газовым термометром.

Из уравнения 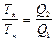следует, что нулем температуры является температура, при которой количество теплоты Q₂=0.

В этом случае КПД цикла Карно должен равняться единице. Так как большим он стать не может (по первому началу термодинамики), то эта температура наинизшая. Напомним, что абсолютный нуль температуры - это t=–273,15^°. Согласно второму началу термодинамики невозможно получить КПД тепловой машины, равный единице, поэтому можно дать еще одну формулировку второго начала термодинамики: абсолютный нуль температуры принципиально недостижим, хотя к нему можно приблизиться сколь угодно близко. В настоящее время уже получена температура, составляющая 0,0001 К.

Энтропия

Все формулировки второго начала термодинамики сводятся к тому, что самопроизвольные процессы необратимы, т.е. не могут протекать в обратном порядке без изменения состояния окружающих тел.

Необратимость тепловых процессов с молекулярно-кинетической точки зрения объясняется их вероятностным характером. Равновесное состояние осуществляется наибольшим числом способов реализации этого состояния. В качестве примера рассмотрим систему, состоящую из четырех частиц газа: a, b, c, d (рис. 8.9). Эти частицы находятся в объеме, разделенном мысленно на две равные ячейки, и могут свободно в них перемещаться.

Состояние системы, определяемое числом частиц в первой и второй ячейках, назовем макросостоянием; состояние системы, определяемое тем, какие конкретно частицы находятся в каждой из ячеек, - микросостоянием. Тогда (рис. 8.9.а) макросостояние – одна частица в первой ячейке и три частицы во второй – осуществляется четырьмя микросостояниями, а макросостояние, соответствующее размещению четырех частиц, равномерно по две в каждой ячейке, - шестью микросостояниями (рис. 8.9, б).

Термодинамической вероятностью W_тер называют число способов размещения частиц или микросостояний, реализующих данное макросостояние.

В приведенных выше примерах W_тер=4 в первом случае и W_тер=6 во втором. Очевидно, что равномерному распределению частиц по ячейкам (по две) соответствует большая термодинамическая вероятность. С другой стороны, равномерное распределение частиц отвечает равновесному состоянию. Из теории вероятности известно, что система, предоставленная самой себе, стремится прийти к макросостоянию, которое реализуется наибольшим количеством способов, наибольшим количеством микросостояний, т.е. к состоянию с наибольшей термодинамической вероятностью.

Таким образом, количественной характеристикой теплового состояния является термодинамическая вероятность. Однако принято вместо W_тер пользоваться величиной

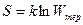(8.10.1)

называемой энтропией системы.

Соотношение (8.10.1), характеризующее связь энтропии и термодинамической вероятности называется формулой Больцмана. Отсюда определение энтропии: энтропия – скалярная физическая величина, характеризующая макросостояние термодинамической системы, и численно равная постоянной Больцмана, умноженной на 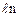термодинамической вероятности этого состояния.

Соответственно второе начало термодинамики может быть сформулировано так: все естественные процессы в изолированной термодинамической системе протекают так, что система переходит от состояний, менее вероятных, к состояниям, более вероятным.

Изменение термодинамической вероятности .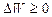

Понятие энтропии впервые было введено Р.Клаузиусом в 1862 году. Для выяснения физического содержания этого понятия рассматривают отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, называемое приведенным количеством теплоты:

dS = 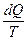, (8.10.2)

где dQ –бесконечно малое количество теплоты, сообщенное системе в элементарном обратимом процессе.

Для произвольного процесса приведенное количество теплоты равно:

ΔS =S₂ - S₁= 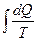, (8.10.3)

где dQ – количество теплоты, сообщенное системе на элементарном участке процесса теплоотдающим телом, температура которого Т; S₁ и S₂ – значения энтропии в состояниях 1 и 2, DS – изменение энтропии в течение обратимого процесса. Изменение энтропии в любом обратимом процессе, переводящем систему из состояния 1 в состояние 2, равно приведенному количеству теплоты, переданному системе в этом процессе.

Изменение энтропии системы, с учетом (8.10.1):

,

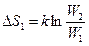где W₁ и W₂ - значения термодинамической вероятности в состоянии 1 и 2.

Каждому состоянию тела соответствует одно определенное значение энтропии. Поэтому энтропия является однозначной функцией состояния. Физический смысл имеет не сама энтропия, а лишь разность энтропий.

Р. Клаузиусом были получены следующие важные положения, которые сформулируем без доказательства:

1. Энтропия является аддитивной величиной: энтропия системы из нескольких тел является суммой энтропий всех тел.

2. Энтропия определяется только с точностью до произвольной постоянной.

3. Если в изолированной системе происходят обратимые процессы, то ее энтропия остается неизменной .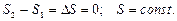

4. Энтропия изолированной системы при протекании необратимого процесса возрастает. Энтропия изолированной системы не может уменьшаться ни при каких процессах.

5. Энтропия системы, находящейся в равновесном состоянии, максимальна.

Математически эти положения можно записать в виде неравенства называемогонеравенством Клаузиуса:

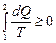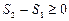или (8.10.4)

В природе все реальные процессы являются необратимыми. Поэтому можно утверждать, что все процессы в конечной изолированной системе ведут к увеличению энтропии. Это принцип возрастания энтропии. Основываясь на вышеизложенном, можно так сформулировать второе начало термодинамики: в изолированных системах возможны лишь такие процессы, при которых энтропия не убывает. Она постоянна, если процессы обратимы, и возрастает, если процессы необратимы.

Если система не изолирована, то ее энтропия может вести себя произвольным образом. Если система отдает тепло (DQ<0), то ее энтропия убывает. Если такая система совершает замкнутый цикл, то энтропия в конце цикла буде равна исходному значению, то есть ее изменение равно нулю. Однако на разных этапах энтропия может и убывать, и возрастать, но так, что сумма всех изменений энтропии равно нулю.

Энтропия является мерой беспорядка системы.

Так как энергия беспорядочного движения частиц газа пропорциональна температуре, то при нуле температуры беспорядочное движение должно прекратиться – частицы будут располагаться наиболее упорядоченным образом. Этой наибольшей упорядоченности расположения частиц должна отвечать наименьшая энтропия. В.Нернст (1864-1941), основываясь на ряде физико-химических наблюдений, высказал положение, часто называемое третьим началом термодинамики: энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина:

.

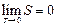Из теоремы Нернста следует, что теплоемкости С_р и С_V при 0 К равны нулю.