Правило эквивалентности прямой последовательности (правило Щедрина) и его применение в расчетах

Из предыдущих параграфов следует, что токи обратной и нулевой последовательностей и напряжения всех последовательностей пропорциональны току прямой последовательности в месте КЗ. Следовательно, задача расчета любого несимметричного КЗ прежде всего состоит в нахождении тока прямой последовательности в месте рассматриваемого вида КЗ.

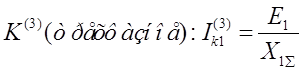
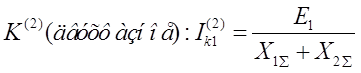
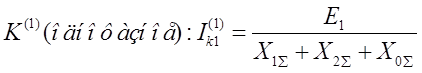
Двухфазное КЗ на землю:

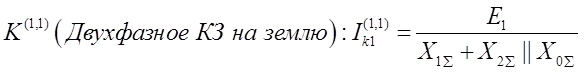
или

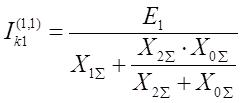
Общая формула для определения тока прямой последовательности может быть записана как:

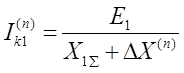, где

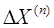-дополнительное сопротивление или сопротивление шунта;

n – вид несимметричного КЗ.

Такая обобщенная запись позволила Н.Н. Щедрину сформулировать следующее важное положение (правило):

Ток прямой последовательности при любом виде КЗ может быть определен как ток при симметричном трехфазном КЗ при условии, что действительная точка КЗ. удалена на дополнительную реактивность

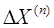, не зависящую от сопротивления схемы прямой последовательности, а определяемую видом повреждения и результирующим сопротивлением схемы обратной и нулевой последовательностей относительно рассматриваемой точки схемы.

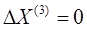
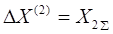
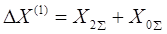
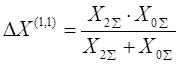
Схемная интерпретация этого положения для разных видов КЗ будет выглядеть следующим образом:

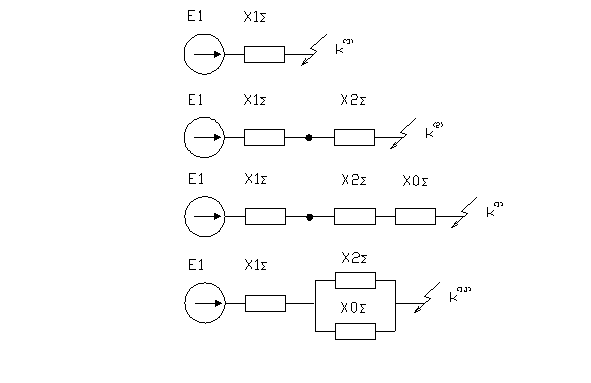
Это положение, которое называют правилом эквивалентности прямой последовательности, справедливо при условии, что рассматривается только основная гармоника тока несимметричного КЗ.

Полные токи для всех видов КЗ:

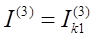
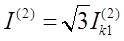
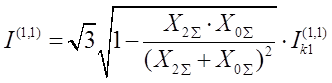
или в общем виде модуль фазного тока в месте любого (n) несимметричного КЗ:

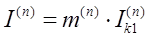
Где m– коэффициент несимметрии (пропорциональности);

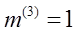
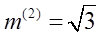
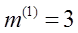
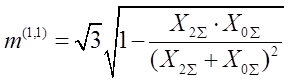
Отсюда вытекают формулы для определения напряжения прямой последовательности:

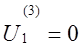
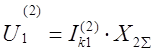
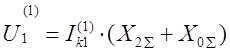
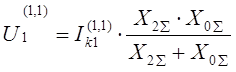
Обобщая все эти выражения можно записать общую формулу для определения напряжения прямой последовательности для любого вида КЗ :

.

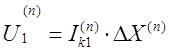Эта формула является следствием из правила эквивалентности прямой последовательности .

Другими словами напряжение прямой последовательности в месте несимметричного КЗ равно падения напряжения от протекания тока прямой последовательности по величине шунта.