Пример расчета рамы на ударную нагрузку

Условие задачи

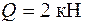На раму, показанную на рис. 7.5, падает груз Q с высоты . Вес груза , поперечное сечение рамы – двутавр № 20. Требуется найти максимальные нормальные напряжения в опасном сечении рамы и прогиб в точке удара от ударного действия нагрузки.

Решение

Чтобы определить динамический коэффициент по формуле (7.4), необходимо найти прогиб 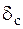точки С (точки приложения нагрузки Q) от статического действия нагрузки. Найдем этот прогиб, используя метод Максвелла – Мора и интегрируя формулу Максвелла – Мора с помощью правила Верещагина. Для этого построим эпюры изгибающих моментов от нагрузки Q (рис. 7.6, а) и от единичной силы, соответствующей искомому перемещению (рис. 7.6, б). Перемножим эти эпюры по правилу Верещагина:

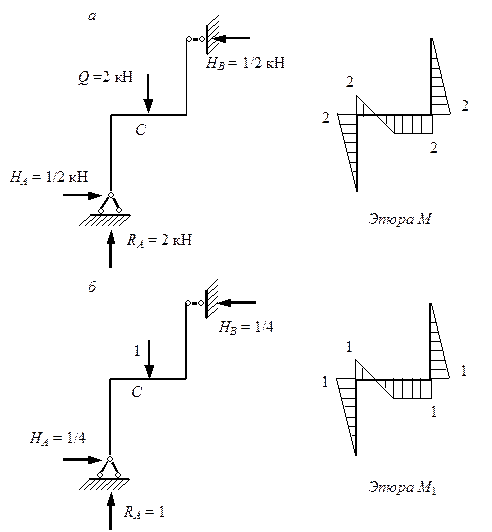Рис. 7.6. Эпюры изгибающих моментов: а – от веса груза Q; б – от единичной силы

.

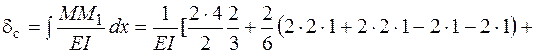
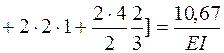Подставляя величину жесткости для двутавра № 20, сосчитаем прогиб в см:

.

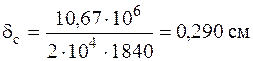Найдем динамический коэффициент по формуле (7.4):

.

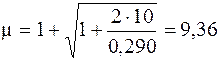Определим максимальные нормальные напряжения в опасном сечении от статического действия нагрузки. В рассматриваемом примере несколько равно опасных сечений с изгибающим моментом 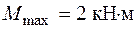. Максимальные статические напряжения

.

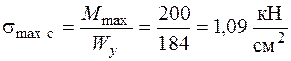Динамические напряжения от действия ударной нагрузки увеличатся согласно формуле (7.5) в 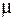раз:

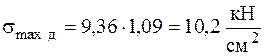.[23]

Во столько же раз увеличится и динамический прогиб:

.

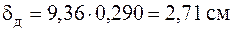СПИСОК ЛИТЕРАТУРЫ

Основная

1. Александров А. В., Потапов В. Д., Державин Б. П. Сопротивление материалов. М.: Высш. шк., 1995.

2. Гастев В. А. Краткий курс сопротивления материалов. М.: Физматгиз, 1977.

3. Дарков А. В., Шпиро Г. С. Сопротивление материалов. М.: Высш. шк., 1989.

4. Сопротивление материалов: Метод. указания и схемы заданий к расчетно-графическим работам для студентов всех специальностей / СПбГАСУ; Сост: И. А. Куприянов, Н. Б. Левченко, Шульман Г.С.. СПб., 2010.

5. Сопротивление материалов: Учебное пособие по выполнению расчетно-графических работ. Ч. 1. / Н. Б. Левченко, Л. М. Каган-Розенцвейг, И. А. Куприянов, О. Б. Халецкая; СПбГАСУ. СПб., 2011.

1. Сопротивление материалов: Учебное пособие по выполнению расчетно-графических работ. Ч. 2. / Н. Б. Левченко; СПбГАСУ. СПб., 2011.

1. Дополнительная

1. Феодосьев В. И. Сопротивление материалов. М.: Наука, 1970.

1. Строительная механика. Под ред. Даркова А. В. М.: Высш. шк., 1976.

1. Иванов Н. М. Детали машин. М.: Высш. шк., 1998.

1.

1. СОДЕРЖАНИЕ

1. Общие указания по выполнению расчетно-графических работ.....................

1. Используемые обозначения.......................................................................................

1. 5. СЛОЖНОЕ СОПРОТИВЛЕНИЕ.......................................................................

1. 5.1. Расчет балки, подверженной косому или пространственному изгибу................................................................................................................................

1. Пример расчета балки при пространственном изгибе (задача № 28)............................................................................................................

1. 5.2. Внецентренное растяжение-сжатие стержней большой жесткости..............................................................................................................................

1. 5.2.1. Определение моментов инерции сложных сечений относительно главных центральных осей (задачи № 29, 30, 31).................................................

1. Примеры решения задач ................................................................................

1. Пример 1. Определение моментов инерции сечения, имеющего одну ось симметрии..................................................................................................................

1. Пример 2. Определение моментов инерции несимметричного сечения.......

1. 5.2.2. Определение грузоподъемности жесткого стержня моносимметричного сечения при внецентренном растяжении-сжатии (задача № 29)...................

1. 5.2.3. Определение грузоподъемности внецентренно сжатых жестких стержней несимметричных сечений (задачи № 30, 31)..........................................

1. 5.3. Общий случай сложного сопротивления..................................................

1. Примеры решения задач......................................................................................

1. 5.3.1. Расчет стержня в общем случае сложного сопротивления (задача № 32)...............................................................................................................

1. 5.3.2. Расчет коленчатого вала на изгиб с кручением (задача № 33).............

1. Пример расчета коленчатого вала....................................................................

1. 6. УСТОЙЧИВОСТЬ................................................................................................

1. Примеры решения задач.............................................................................................

1. 6.1. Определение грузоподъемности центрально-сжатого стержня (задача № 34)..............................................................................................................

1. 6.2. Подбор сечения центрально-сжатого стержня (задача № 35).....................

1. Пример 1...............................................................................................................

1. Пример 2................................................................................................................

1. 6.3. Расчет гибкого сжато-изогнутого стержня (задача № 36)...........................

1. Пример расчета гибкого сжато-изогнутого стержня..........................................

1. 7. РАСЧЕТ НА ДИНАМИЧЕСКУЮ НАГРУЗКУ...............................................

1. 7.1. Вынужденные колебания систем с одной степенью свободы (задача № 37).............................................................................................................

1. Пример расчета системы с одной степенью свободы

1. 7.2. Расчет рамы (балки) на ударную нагрузку (задача № 38)...........................

1. Пример расчета рамы на ударную нагрузку........................................................

1. Список литературы...............................................................................................

1.

1.

1.

1.

1. Нина Борисовна Левченко

1.

1.

1.

1. СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

1.

1. Часть 3

1.

1.

1.

1.

1.

1. Редактор А.В. Афанасьева

1. Корректор К.И. Бойкова

1. Компьютерная верстка И.А. Яблоковой

1.

1.

1.

1.

1.

1.

1.

1.

1.

1.

1.

1. Подписано к печати 10.10.2002. Формат 60х84 1/16. Бум. офсетная.

1. Усл. печ. л. . Уч.-изд. л. . Тираж 500. Заказ . "С"

1. Санкт-Петербургский государственный архитектурно-строительный

1. университет. 198005, Санкт-Петербург, 2-я Красноармейская ул., д. 4.

1. Отпечатано на ризографе. 198005, Санкт-Петербург, 2-я Красноармейская ул., д. 5.

1.

6.

[1] Сечение может иметь произвольную форму, но должно быть однородным по материалу.

[2] Поскольку касательные напряжения от поперечных сил не учитываем, допустимо строить только эпюры изгибающих моментов.

[3] Эта часть задачи носит академический характер.

[4] Отметим, что для балки прямоугольного сечения отношение 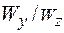является известной величиной и зависит от расположения сечения. Если в опасном сечении 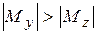, то при рациональном расположении сечения наибольшая сторона 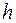должна быть перпендикулярна оси 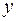, 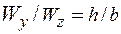и условие прочности 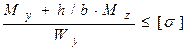, где 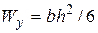. Если в опасном сечении 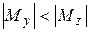, то сторону 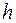выгодно разместить параллельно 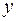, а условие прочности тогда записывается так: 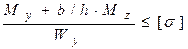, где .

[5] Эпюру М₁ от горизонтальной единичной силы, направленной вдоль оси y, можно не строить, так как она такая же, как от вертикальной единичной нагрузки.

[6] При составлении уравнения нейтральной линии не забывайте учитывать знаки изгибающих моментов в рассматриваемом сечении. В данной задаче оба момента положительны.

[7] При внецентренном растяжении-сжатии знак изгибающего момента можно определить и по-другому, а именно: 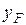и 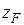следует считать координатами точки приложения силы и, следовательно, учитывать их знаки. С учетом знаков надо брать и величины сил, принимая, что растягивающие силы – положительны, а сжимающие – отрицательны. На рис. 5.9 обе координаты точки приложения силы 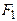положительны. У сжимающей силы 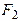на рис. 5.9 координата , .

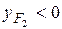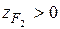[8] Не забывайте правильно подставлять единицы измерения. Множитель перед 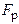в данном примере имеет размерность см^-2.

[9] Допускается координаты точки в главных осях не вычислять, а только измерять на рисунке.

[10] Вообще говоря, для проверки прочности стержней круглого и прямоугольного сечений нет необходимости в точном определении положения опасных точек, но в учебных целях для понимания используемых формул мы все же найдем положение этих точек.

[11] Касательные напряжения, вызванные действием поперечных сил, в круглом сечении из-за сложности их точного определения в опасных точках и малости их величины допускается не учитывать.

[12] На рис. 5.28, б показано направление оси х, важное для определения знаковпоперечных сил; его необходимо сохранять для всех участков.

[13] Задача предложена И.А. Куприяновым.

[14] Расчетным считаем правый кривошип, так как в нем крутящий момент не равен нулю.

[15] Поскольку при изучении курса сопротивления материалов для обеспечения прочности студенты используют расчет по допускаемым напряжениям, то нельзя брать значения коэффициентов продольного изгиба из таблиц, приведенных в современных СНиП, где используется другой подход к проверке прочности.

[16] Материалу сталь С235 соответствует в таблице сталь Ст.3, стали С275 – Ст.5.

[17] При выполнении расчетно-графической работы студенту предлагается условно принять площадь ослаблений, составляющую 15% от полной площади.

[18] Заметим, что, если в сортаменте выбрать уголок с более толстой полкой, но с примерно такой же площадью, например, уголок 160´12 (А_уг = 37,4 см²), минимальный радиус инерции сечения из двух таких уголков будет i_min = 6,23 см и гибкость стержня будет на 13% больше, чем для уголка 180´11.

[19] Для сечений из прокатных профилей добиться желаемой экономичности (подобрать сечение так, чтобы расчетное напряжение отличалось от допускаемого не больше, чем на 5 %) не всегда удается, т.к. размеры сечения имеют дискретные значения.

[20] Как обычно, пренебрегаем горизонтальным перемещением точек оси балки и, считая массу сосредоточенной, ее поворотом.

[21] Задача предложена И.А. Куприяновым.

[22] Попытки уменьшить динамические напряжения, увеличив размер сечения, не проносят нужного эффекта, так как при увеличении размера сечения увеличивается жесткость, статический прогиб уменьшается, а динамический коэффициент увеличивается.

[23] Видно, что динамические напряжения не превосходят предела пропорциональности s_пц =200 МПа, и материал работает упруго.