Пример расчета гибкого сжато-изогнутого стержня

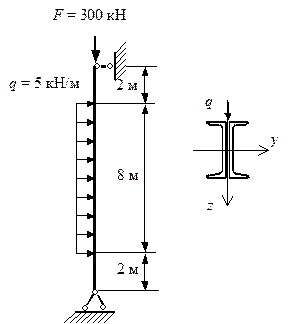Рис. 6.6. Сжато-изогнутый стержень

Условие задачи

Стержень, показанный на рис. 6.6, сжимается силой F = 300 кН и изгибается поперечной нагрузкой q = 5 кН/м. Сечение стержня состоит из двух швеллеров, выполненных из стали С235 с 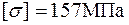. Требуется подобрать номер швеллера так, чтобы удовлетворялись условия прочности и жесткости по деформированному состоянию, а также условие устойчивости в плоскости наименьшей жесткости. Допускаемый прогиб примем равным .

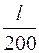Решение

Построим эпюру изгибающих моментов от поперечной нагрузки (рис. 6.7, а) и подберем сечение расчетом по недеформированному состоянию без учета продольной силы.

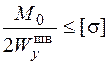, откуда .

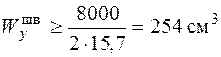Выберем из сортамента прокатной стали швеллер № 27, у которого 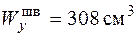, , 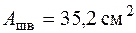и проверим прочность с учетом продольной силы:

.

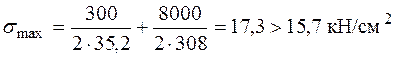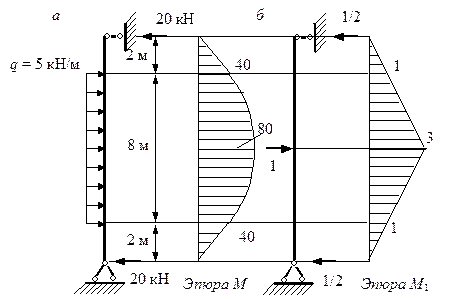Рис. 6.7. Эпюры изгибающих моментов: а – от поперечной нагрузки; б – от единичной силы, соответствующей прогибу в середине пролета

Увеличим размер швеллера. Для швеллера № 30 с такими характеристиками: 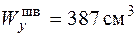, , 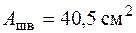, 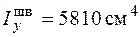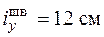– условие прочности по недеформированному состоянию выполняется:

.

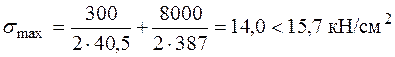Проверим прочность по деформированному состоянию. Найдем максимальный прогиб в середине пролета, перемножая эпюры М от поперечной нагрузки и М₁ от единичной силы (рис. 6.7, б):

.

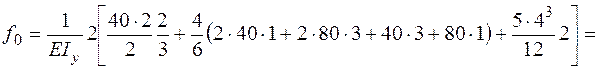
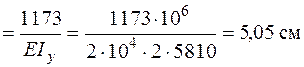Найдем критическую силу по формуле Эйлера (6.2). Момент инерции принимаем равным 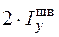, что соответствует изгибу в плоскости действия поперечной нагрузки (плоскости максимальной жесткости)

.

.

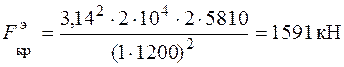Принимая коэффициент запаса прочности n = 1,5, проверим прочность по условию прочности по деформированному состоянию (6.11).

.

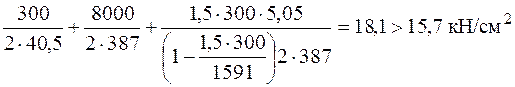Поскольку условие прочности по деформированному состоянию для швеллера № 30 не выполняется, проверим прочность по условию (6.11) для швеллера № 33, у которого 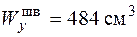, , 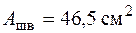, , 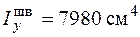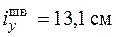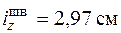. Прогиб

.

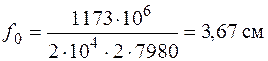Критическая сила

.

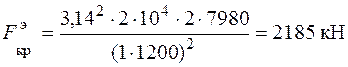Тогда условие прочности (6.11) выполняется:

.

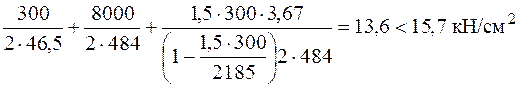Проверим жесткость стержня расчетом по деформированному состоянию по формуле (6.12). Примем 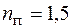и допускаемый прогиб 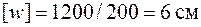. Тогда условие жесткости выполняется:

.

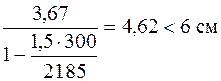Осталось удовлетворить третьему условию – условию устойчивости в плоскости наименьшей жесткости. Найдем минимальный радиус инерции сечения из двух швеллеров:

.

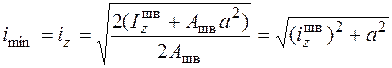Если швеллеры расположены вплотную друг к другу, то 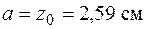. Тогда

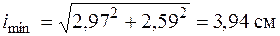
и

.

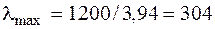Гибкость стержней больше, чем 200, не допускается. Для сечения из двух швеллеров можно уменьшить гибкость, не увеличивая размер швеллера. Для этого следует раздвинуть швеллеры. Величину а нужно подобрать так, чтобы гибкость стержня была меньше 200 и условие устойчивости (6.6) выполнялось. В рассматриваемом примере такой величиной будет 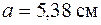, которой соответствует расстояние между стенками швеллеров 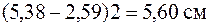. Для стержня с таким сечением

;

.

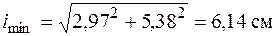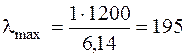Этой гибкости соответствует 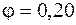, и условие устойчивости выполняется:

.

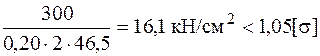Таким образом, всем условиям (прочности, жесткости и устойчивости) удовлетворяет сечение из двух швеллеров № 33, расстояние между стенками которых равно 5,60 см.