Сверхпроводник в магнитном поле
В 1933 г. В. Мейсснер и Р. Оксенфельд, изучая распределение магнитного потока вокруг оловянных и свинцовых образцов, охлажденных в магнитном поле до температуры их сверхпроводящих переходов, обнаружили, что магнитный поток выталкивается из образца при Т<ТС. Таким образом, сверхпроводник ведет себя, как идеальный диамагнетик, где магнитная индукция B à 0. Это же явление было зарегистрировано и для других сверхпроводников. Явление, заключающееся в том, что внутри сверхпроводника магнитная индукция равна нулю, получило название эффекта Мейсснера-Оксенфельда.
Рассмотрим подробнее данный эффект. Поместим сверхпроводник в однородное магнитное поле при температуре больше критической. Индукция магнитного поля внутри сверхпроводника пропорциональна напряженности внешнего поля H:
B=μμ0H, (1.4)
где μ – магнитная проницаемость материала;
μ0 – магнитная постоянная.
Поскольку материал не является ферромагнетиком (μ ≈ 1), поле внутри сверхпроводника практически не искажается (рис. 1.3, а).
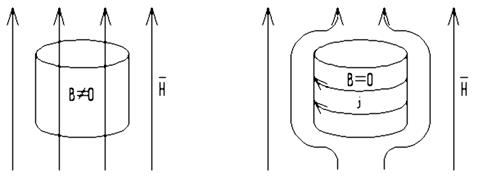
а) б)
Рис. 1.3. Сверхпроводник в магнитном поле H: а) Т>ТС, б) Т<ТС
Теперь охладим сверхпроводник до температуры Т<ТС. Если поле H недостаточно сильное, будет наблюдаться эффект Мейсснера: внутри сверхпроводника установится состояние с B=0 (рис. 1.3, б). Это значит, что на поверхности сверхпроводника появились циркулирующие сверхпроводящие токи j, которые в объеме создают встречное магнитное поле индукции –B. Такое состояние является термодинамически равновесным, т.е. оно устанавливается при любой последовательности операций охлаждения и включения магнитного поля и остается стабильным, пока не изменяются поле или температура.
Поверхностный характер сверхпроводящих токов обусловлен вторым уравнением Максвелла:
rot B=j. (1.5)
Поскольку поле B в условиях эффекта Мейсснера в образце отсутствует, rot B также обращается в нуль. Из (1.5) следует, что в этом объеме отсутствуют и токи j. Однако магнитное поле не может быть вытолкнуто из всего объема сверхпроводника до самой поверхности, т.к. это привело бы к скачку магнитного поля от 0 до величины B и существованию бесконечно больших поверхностных токов. Следовательно, магнитное поле проникает в приповерхностный слой сверхпроводника на некоторую глубину λ – глубину проникновения. В этом же слое текут и сверхпроводящие токи. Для оценки глубины проникновения используют следующее выражение:
B(x)=B(0)exp(-x/λ), (1.6)
где B(0) – индукция магнитного поля вне сверхпроводника;
B(x) – индукция магнитного поля внутри сверхпроводника;
x – текущая координата.
Теория сверхпроводимости дает оценку для глубины проникновения:
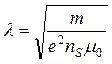 , (1.7)
, (1.7)
где m – масса электрона.
Решение уравнения (1.6) в виде графика приведено на рис. 1.4.
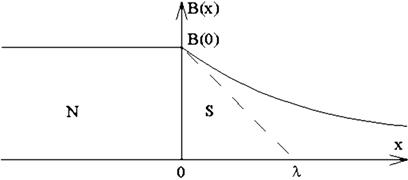
Рис. 1.4. Распределение магнитного поля вне (N) и внутри (S) сверхпроводника
Оценка величины λ для большинства сверхпроводников имеет порядок 10-5 – 10-6 см.
В случае протекания высокочастотного тока по проводнику наблюдается скин-эффект: выталкивание тока на приповерхностный слой. Эффект вызван взаимодействием (отталкиванием) токов. На первый взгляд, между скин-эффектом и эффектом Мейсснера имеется аналогия. Нужно заметить, что аналогия имеет место чисто формальная, поскольку сверхпроводящие токи – постоянные. Механизм эффекта Мейсснера имеет иную природу – квантовую и будет обсуждаться ниже.
Эффект Мейсснера позволяет сверхпроводнику в неоднородном магнитном поле левитировать, т.е. висеть без опоры и подвеса сколь угодно долго. Это явление лежит в основе “магнитной подушки”, движения, например, железнодорожного вагона над опорной плоскостью. В этом случае трение практически отсутствует. Экспериментальная ветка железной дороги на магнитной подушке испытывается в Японии.
При рассмотрении эффекта Мейсснера выше уже была сделана оговорка о недостаточно сильном магнитном поле. Имелось в виду сохранение сверхпроводящего состояния, поскольку существует критическое поле НС, превышение которого приводит к нарушению сверхпроводимости. Взаимодействие нормальных или сверхпроводящих электронов с магнитным полем определяет энергию системы. Если в слабом поле Н<НС энергетически выгодным является сверхпроводящее состояние, то в сильном поле Н>НС таким состоянием становится нормальное. Так появляется третий критический параметр сверхпроводника – критическая напряженность НС. Критическая напряженность поля НС(Т) уменьшается с ростом температуры, т.е. тепловой и магнитный факторы усиливают друг друга:
НС(Т)=НС(0)[1-(Т/ТС)2], (1.8)
где НС(0) – критическая напряженность при нулевой температуре.
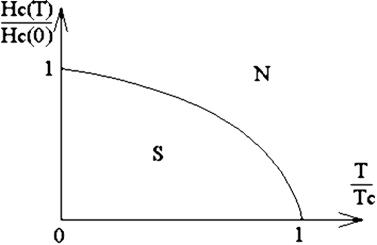
Рис. 1.5. Область нормального N и сверхпроводящего S состояния
Значения напряженности критического поля для различных сверхпроводников имеют разные значения (табл. 1.2).
Таблица 1.2
Значения напряженности критического поля
| Материал | НС(0), А/м | Материал | НС(0), А/м |
| алюминий | 0,79 | осмий | 0,5 |
| кадмий | 0,24 | рений | 1,6 |
| галлий | 0,41 | тантал | 6,6 |
| индий | 2,2 | таллий | 1,4 |
| ртуть | 3,3 | олово | 2,4 |
Необходимо отметить, что величина критического поля будет зависеть также и от формы сверхпроводника, и его ориентации в магнитном поле [2].
Выталкивание магнитного потока из сверхпроводника, которое обсуждалось выше, имеет место в том случае, если сверхпроводниковый образец является односвязанным (сплошным). Если же образец имеет полость, например, сверхпроводниковое кольцо, картина изменится. При охлаждении в магнитном поле до Т<ТС поток будет вытолкнут из сверхпроводника, однако он останется в полости. Ранее было установлено, что выталкивание магнитного поля происходит за счет возникающих сверхпроводящих токов j, создающих противополе. Поскольку магнитный поток в полости существует, очевидно, существуют его создающие токи j2,направленные встречно токам j1 (рис. 1.6).
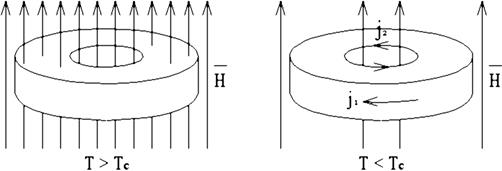
Рис. 1.6. Выталкивание магнитного поля
Поскольку сопротивление в сверхпроводнике отсутствует, токи будут незатухающими. Если выключить внешнее магнитное поле, магнитный поток внутри кольца станет поддерживаться незатухающими токами.
Ф. Лондон предположил, что захваченный магнитный поток Ф должен быть равен целому числу квантовпотока Ф0, то есть:
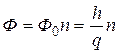 , (1.9)
, (1.9)
где n – целое число;
q – заряд;
h – постоянная Планка.
Впоследствии это предположение было экспериментально подтверждено, однако заряд q оказался равен удвоенному заряду электрона:
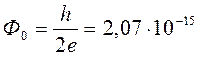 Вб. (1.10)
Вб. (1.10)
Этот факт говорит о том, что частицы, состоящие из двух электронов есть не что иное, как куперовские пары. Вероятно, что величина n в (1.9) связана с квантовым числом куперовских пар. Как уже отмечалось, поведение сверхпроводящего конденсата (куперовских пар) жестко коррелировано и при переходе в следующее состояние, с иным квантовым числом, все пары должны перейти в это состояние.
Квантование магнитного потока в кольце представляет собой пример макроскопического квантового эффекта.
Такое кольцо можно рассматривать как систему, имеющую n возможных стационарных состояний, и использовать в соответствующих условиях.
Дата добавления: 2016-11-29; просмотров: 4016;











