Энергетическая щель. Одночастичное туннелирование
Рассмотрим энергетический спектр электронов сверхпроводника. Для металлов в нормальном состоянии этот спектр является сплошным (рис. 1.9, а) и описывается выражением:
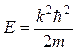 , (1.15)
, (1.15)
где k – волновой вектор.
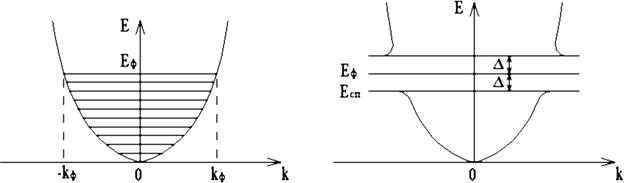
а) б)
Рис. 1.9. Энергетический спектр электронов
Электроны, согласно распределению Ферми-Дирака, располагаются ниже уровня Ферми (EФ), занимая энергетические уровни в соответствии с постулатом Паули: на одном энергетическом уровне два электрона с противоположными спинами. Выше уровня Ферми при низких температурах электронов нет. Для металлов такая картина справедлива и при комнатных температурах. В случае какого-либо возбуждения (электрическое поле, излучение) электроны “перемещаются” выше уровня Ферми, а на их уровне остаются вакансии.
Как уже отмечалось, при переходе в сверхпроводящее состояние часть электронов образует пары и перестает подчиняться постулату Паули. Очевидно, что энергетический спектр электронов изменяется. Спариваются электроны, близкие к уровню Ферми, поскольку они имеют энергетические “степени свободы”, могут менять энергию свободного на энергию связанного в паре электрона. Концентрация таких электронов составляет ~10-4 от общей концентрации. При образовании куперовских пар энергия системы уменьшается на величину энергии связи EСВ электронов в паре, поэтому в энергетическом спектре электронов появляется энергетическая щель шириной 2D (рис. 1.9, б):
EСВ=2D. (1.16)
Энергетическая щель отделяет уровень EСП, где находятся куперовские пары от области, где пары распадаются на отдельные электроны. Для перехода в эту область необходима энергия, равная EСВ – энергии связи пары. Величина этой энергии (ширина щели) зависит от температуры сверхпроводника и при Т=ТС обращается в нуль.
При Т ≈ 0 К ширина энергетической щели максимальна и пропорциональна критической температуре:
2D(0)=3,5kТС, (1.17)
где k – постоянная Больцмана.
Существование энергетической щели в сверхпроводниках получило экспериментальное подтверждение, в частности, при измерении спектра поглощения сверхпроводника в дальней ИК области. При Т ≈ 0 К поглощения не происходит до тех пор, пока энергия квантов hν<2D. При частоте ν, для которой hν=2D, начинается интенсивное поглощение излучения. Энергия 2D затрачивается на разрыв пары, и электроны переходят в свободное состояние над щелью, становясь независимыми друг от друга. Величина щели составила 10-3-10-2 эВ (табл. 1.4).
Наличие щели в энергетическом спектре сверхпроводников напоминает существование запрещенной зоны в полупроводниках с той разницей, что щель не связана с кристаллической решеткой, и в электрическом поле она смещается вместе с поверхностью Ферми в отличие от запрещенной зоны.
Таблица 1.4
Величина щели для различных сверхпроводников
| Материал | λ, нм | ξ, нм | Материал | λ, нм | ξ, нм |
| алюминий | 16-50 | 1360-1600 | ниобий | 240-354 | |
| кадмий | свинец | 39-63 | 61-96 | ||
| ртуть | 38-45 | - | олово | 34-75 | 100-300 |
| индий | 36-64 | 240-354 | таллий | - |
Наличие энергетической щели является определяющим фактором в формировании состояния сверхпроводимости, в существовании незатухающих сверхпроводящих токов. В туннельно-прозрачных контактах наличие энергетической щели приводит к появлению любопытных эффектов, которые находят практические применения. Это – туннелирование электронов через потенциальный барьер-диэлектрик, иначе говоря, одночастичное туннелирование. Обычно различают три вида туннелирования, имеющие практическое значение при разработке приборов: туннельный переход в структуре металл-диэлектрик-сверхпроводник (МДС), переход в структуре сверхпроводник-диэлектрик-сверхпроводник (СДС), переход в структуре С1ДС2, при наличии двух различных сверхпроводников с различными энергетическими щелями. На рис. 1.10 приведены энергетические диаграммы и вольт-амперные характеристики туннельных структур (Т ≈ 0 К ).
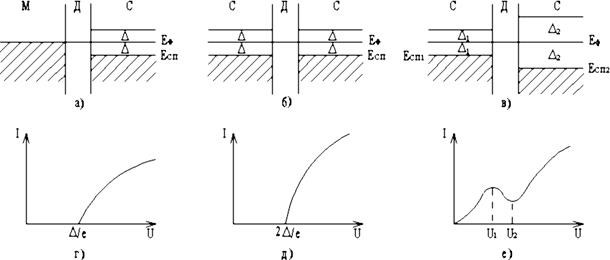
Рис. 1.10. Энергетические диаграммы (а-в) и вольт-амперные характеристики:
а, г – МДС; б, д – СДС; в, е – С1ДС2-структура
Известно, что приложение разности потенциалов U к структуре вызовет смещение уровней Ферми и других уровней на величину eU, так что относительное положение уровней изменится и будет возможно туннелирование через диэлектрик. Эти смещения различны: для структуры МДС они составляют D/e, для структуры СДС – 2D/e и определяют начала вольт-амперных характеристик. Для структуры С1ДС2 картина оказывается более сложной и вольт-амперная характеристика проходит через точки U1=(D2-D1)/e и U2=(D2+D1)/e. Наибольший интерес вызвало наличие на ВАХ С1ДС2-структуры участка отрицательного дифференциального сопротивления.
Эффекты Джозефсона
В разделе 1.4 мы кратко рассмотрели туннелирование электронов в структуре СДС. Возникает вопрос, возможно ли туннелирование куперовских пар?
В 1962 г. Б. Джозефсон в результате вычислений пришел к выводу, что туннельный ток пар IS не только возможен, но и сопоставим по величине с одночастичным током. Максимальное значение IS можно определить из выражения:
Im=πΔ/(2eRN), (1.18)
где RN – сопротивление туннельного контакта в нормальном состоянии.
Из вычислений следовало, что постоянный ток IS должен протекать в отсутствие разности потенциалов на контакте, причем этот ток определяется разностью фаз волновых функций сверхпроводящих конденсатов в одном и другом сверхпроводнике. Джозефсон предсказал и другие свойства структуры, которые впоследствии были обнаружены экспериментально. Рассмотрим процессы, протекающие в структуре СДС, если диэлектрический зазор составляет порядка 1 нм (рис. 1.11, а).
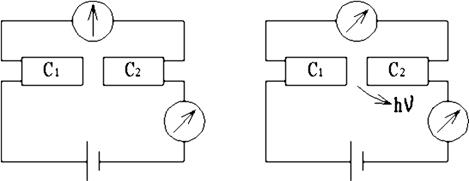
а) б)
Рис. 1.11. Эффект Джозефсона: а – стационарный, б – нестационарный
Подадим на СДС структуру разность потенциалов, через нее потечет ток, падение напряжения на структуре (сопротивление) будет равно нулю. Структура ведет себя, как сплошной сверхпроводящий образец. Ток протекает и по диэлектрическому зазору беспрепятственно. Это явление получило название стационарного эффекта Джозефсона.
При увеличении тока наступает такой момент, когда на структуре возникает постоянная разность потенциалов и одновременно из зазора исходит электромагнитное излучение высокой частоты (см. рис. 1.11, б). Очевидно, кроме постоянного появляется переменный ток высокой частоты. Это явление называют нестационарным эффектом Джозефсона.
Напомним, что, волновая функция куперовской пары является суперпозицией состояний с противоположными k, близкими по значению к kФ. Волновые функции пар совпадают, поскольку пары являются бозонами. Таким образом, все куперовские пары находятся в одном квантовом состоянии и описываются одной функцией. Изменение концентрации влияет не только на амплитуду волновой функции. Волновая функция куперовских пар может быть определена:
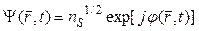 , (1.19)
, (1.19)
где 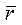 – радиус-вектор;
– радиус-вектор;
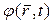 – фаза;
– фаза;
nS – концентрация куперовских пар.
Поскольку движение всех пар строго коррелировано и центры масс всех пар движутся с одинаковым импульсом, то общий импульс электронной сверхпроводящей системы равен P:
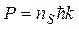 . (1.20)
. (1.20)
Фаза функции (1.19) определяется из выражения:
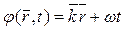 .
.
Волновые функции сверхпроводящих электронов проникают в зазор вследствие туннелирования и определяют функцию в промежуточном слое:
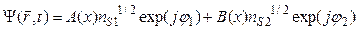 , (1.21)
, (1.21)
где A(x) и B(x) определяют глубину проникновения волновых функций в зазор.
При x=0 A(0)=1 и с ростом x быстро уменьшается до нуля; аналогично при x=d (d – толщина зазора) B(d)=1 и при x<d быстро уменьшается до нуля.
Плотность вероятности волновой функции (1.21) определяется по известной формуле и может быть записана как
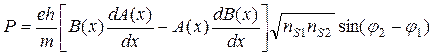 . (1.22)
. (1.22)
Из (1.22) может быть получено выражение для плотности тока туннелирования куперовских пар:
jS=jmsin(φ2-φ1)= jmsinθ, (1.23)
где θ – разность фаз волновых функций пар по обе стороны барьера.
Уравнение (1.23) иногда называют уравнением Джозефсона. Другое важное уравнение Джозефсона связывает напряжение на барьере со скоростью изменения разности фаз:
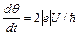 . (1.24)
. (1.24)
Используя выражения (1.23) и (1.24), можно найти мощность (UjS) а затем, с помощью интегрирования по времени, найти энергию контакта:
E(θ)=-(ħIm/2|e|)cosθ. (1.25)
Вольт-амперная характеристика перехода Джозефсона объединяет оба эффекта (рис. 1.12).
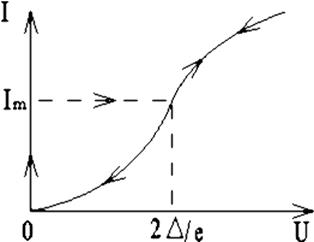
Рис. 1.12. ВАХ переходов Джозефсона. Стрелками показано направление тока
На начальном участке ВАХ (0-Im) ток IS через переход растет, его напряжение остается равным нулю. Этот участок соответствует стационарному эффекту, здесь происходит туннелирование пар через потенциальный барьер. Поскольку падения напряжения нет, нет и сдвига в энергетической диаграмме (рис. 1.13, а) уровни ЕСП в одном и другом сверхпроводнике находятся на одной высоте – между ними возможны туннельные переходы.
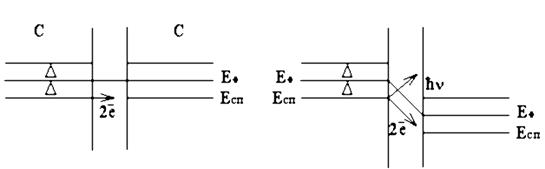
а) б)
Рис. 1.13. Энергетическая диаграмма перехода Джозефсона:
а – стационарный эффект, б – нестационарный эффект
При увеличении тока через переход (IS=Im) наступает такое состояние, что становится возможным одночастичное туннелирование (рис. 1.13, б). Система переходит скачком в это состояние и приобретает падение напряжения:
Um=2D/е. (1.26)
Похожий переход был описан выше (рис. 1.10, д). В связи с изменением энергетической диаграммы закон сохранения энергии пары до и после перехода нарушается, поскольку энергия пары в зависимости от направления перехода либо возрастает, либо убывает. В отсутствие фононов такой энергии (Т<ТС) разница энергии пары либо поглощается, либо выделяется в виде кванта электромагнитного излучения с частотой
ω=2eU/ħ. (1.27)
Туннельный ток куперовских пар из постоянного (стационарный эффект) становится переменным, частота которого определяется выражением:
I= Imsin[(2eU/ħ)t]. (1.28)
Если U=1 мВ, то частота составит 485 ГГц, что соответствует длине волны l ≈ 0,6 мм. Таким образом, переход Джозефсона может служить в качестве генератора СВЧ колебаний с возможностью перестройки частоты.
Далее на ВАХ возрастают и ток, и напряжение, однако обратный ход характеристики не совпадает с прямым, т.е. имеет место гистерезис при Т>0, связанный с существованием нормальных электронов.
Необычные результаты дает наложение на переход Джозефсона магнитного поля, параллельно плоскости контакта. Поле сильно изменяет плотность туннельного тока через переход, проникая в зазор. В этом случае сверхпроводящий ток IS становится функцией магнитного потока ФК или, точнее, функцией отношения ФК/Ф0:
ФК/Ф0=2llB/Ф, (1.29)
где l – длина контакта;
l – глубина проникновения поля в сверхпроводник;
В – индукция внешнего поля.
Величина туннельного тока через переход определяется выражением
IS=Im(ФК)sinφ, (1.30)
где
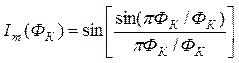 . (1.31)
. (1.31)
Из (1.31) следует, что критический ток перехода Джозефсона осциллирует при изменении внешнего поля, обращаясь в нуль всякий раз, когда отношение (1.29) становится целой величиной (рис. 1.14).
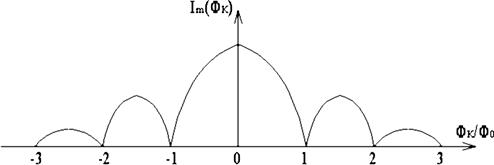
Рис. 1.14. Зависимость критического тока перехода Джозефсона от изменения внешнего поля
Зависимость Im(ФК) позволяет измерять магнитное поле с высокой точностью, поскольку Ф0 очень мало.
Условие обращения в нуль функции Im(ФК) имеет интересную физическую интерпретацию. Оказывается, на переходе образуются магнитные вихри, похожие на вихри Абрикосова. Разница состоит в том, что эти вихри не содержат нормальной фазы в центре, их ось расходится в диэлектрическом зазоре (рис. 1.15). Такие магнитные вихри можно использовать в качестве динамических неоднородностей так же, как вихри Абрикосова, для обработки информации.
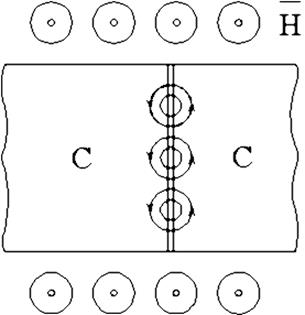
Рис. 1.15. Магнитные вихри на переходе Джозефсона
В заключение необходимо отметить, что эффекты Джозефсона возникают не только в описанной СДС структуре, но и в других структурах, объединяемых общим понятием “слабосвязанные проводники”.
На рис. 1.16 показаны примеры таких структур, используемые в криоэлектронике.
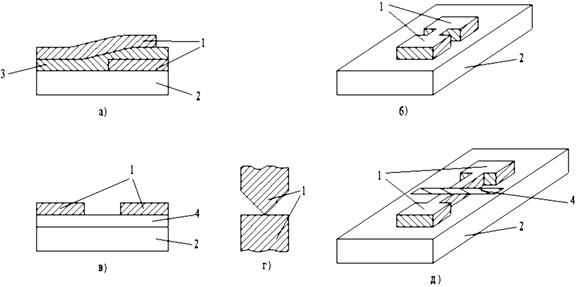
Рис. 1.16. Основные виды слабосвязанных сверхпроводящих структур [4]: а – туннельный переход; б – мостик с микросужением; в – мостик переменной толщины; д – точечный контакт; д – мостик, созданный на эффекте близости. 1 – сверхпроводящие электроды; 2 – подложка; 3 – изолирующий слой; 4 – пленка мостика
Различные типы слабосвязанных структур имеют разные параметры (табл. 1.5). Например, структура “мостик” не имеет гистерезиса, что выгодно отличает ее от структуры СДС.
Таблица 1.5
Параметры слабосвязанных сверхпроводниковых структур, изготовленных методами интегральной технологии
| Материал элемента слабой связи | Структура | d, нм | RN, Ом | Um, мВ | С, пФ |
| диэлектрик | сэндвич | 1-2 | |||
| полупроводник | – v – | 5-50 | 0,1-10 | 0,1 | |
| металл | – v – | 102 | 10-6 | 10-3 | 10-2 |
| полуметалл | мостик | 102 | 0,1-1 | 0,1 | 10-2 |
| металл | – v – | 102 | 0,1 | 0,1 | 10-2 |
| вырожденный полупроводник | планарная | 10-102 | 10-2 | ||
| узкозонный полупроводник | – v – | 102 | 0,5 | 10-3 |
Джозефсоновские переходы находят самое широкое распространение как в аналоговой, так и в цифровой криоэлектронике.
Дата добавления: 2016-11-29; просмотров: 4761;











