Частные производные высшего порядка. Смешанные производные.
Как уже отмечали, что производные 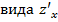 и
и 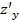 называют частными производными первого порядка или первыми частными производными. Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные, так называемые повторные, производные по x, и y или смешанные частные производные.
называют частными производными первого порядка или первыми частными производными. Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные, так называемые повторные, производные по x, и y или смешанные частные производные.
Так, частные производных второго обозначаются следующим образом:
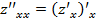 или
или 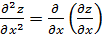 ;
; 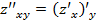 или
или 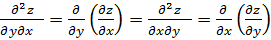 ;
;
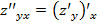 или
или 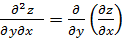 ;
; 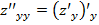 или
или 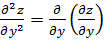 ;.
;.
Аналогично определяются частные производные 3-го, 4-го и более высоких порядков. Например, для функции z=f(x, y) имеем:
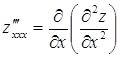 ,
, 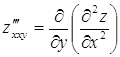 Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными. Для функции
Частные производные второго или более высокого порядка, взятые по различным переменным, называются смешанными частными производными. Для функции 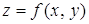 таковыми являются производные
таковыми являются производные 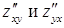 . Заметим, что в случае, когда смешанные производные
. Заметим, что в случае, когда смешанные производные 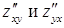 непрерывны, то имеет место равенство
непрерывны, то имеет место равенство 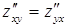 .
.
Пример 5. Найти частные производные второго порядка функции
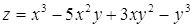 .
.
Решение. Частные производные первого порядка для данной функции найдены в примере 3:
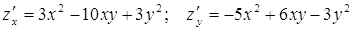
Дифференцируя 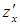 и
и 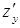 по переменным х и y, получим
по переменным х и y, получим
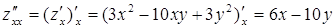 ,
,
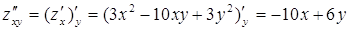 ;
;
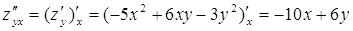 ;
;
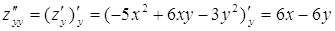 .
.
5. Экстремум функции нескольких переменных. Необходимые и достаточные условия существования экстремума
Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y. Они называютсявторыми частными производными или частными производными второго порядка и обозначаются zxx  , zyy'
, zyy'  , zxy
, zxy  или. Согласно определению
или. Согласно определению 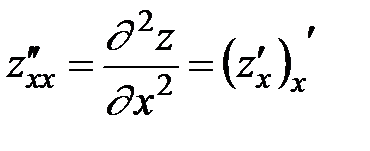 ;
; 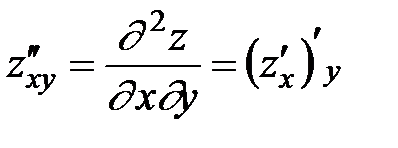 . Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная
. Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная 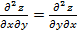 . Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности
. Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности
вычислялись частные производные по x и по y.
Дата добавления: 2016-06-05; просмотров: 8240;











