ТЕПЛОВОЙ РАСЧЕТ РЕКУПЕРАТИВНОГО

ТЕПЛООБМЕННИКА

При расчете теплообменников обычно встречаются два случая: конструктивный расчет с целью определения величины рабочей поверхности теплообменника; проверочный расчет, когда известны поверхность теплообмена и конструкция аппарата, с целью определения температур теплоносителей на выходе из теплообменника и количество передаваемой теплоты.

В обоих случаях основными расчетными уравнениями служат уравнение теплового баланса и уравнение теплопередачи.

Уравнение теплового баланса теплообменника при отсутствии тепловых потерь в окружающую среду и фазовых переходов фор-мулируется следующим образом: тепловой поток Q₁ от теплоотдающего теплоносителя равен тепловому потоку Q₂ к тепловоспринимающему теплоносителю (Q₁ = Q₂ =Q), и записывается так:

Q = m₁c_р1(Т'₁- Т"₁) = m₂c_р2(Т"₂- Т'₂), (6.1)

где m₁ и m₂ – массовые расходы теплоносителей, кг/с;

с_р1 и с_р2 - средние массовые теплоемкости теплоносителей при по-

стоянном давлении в интервале температур от Т' до Т";

Т'₁ и Т'₂ - температуры теплоносителей при входе в аппарат, К;

Т"₁ и Т"₂ - температуры теплоносителей при выходе из аппарата.

Обозначим произведение массового расхода жидкости на среднюю теплоемкость через W, а изменение температуры теплоносителя в пределах теплообменного аппарата через ∆Т, т.е.:

W₁ = m₁c_р1; W₂ = m₂c_р2; ∆Т₁ = Т'₁- Т"₁; ∆Т₂ = Т"₂- Т'₂; (6.2)

Величину W называют условным эквивалентом.

С учетом (6.2) уравнение теплового баланса может быть представлено в следующем виде:

∆Т₁/∆Т₂ = W₂/W₁. (6.3)

Следовательно, изменения температур теплоносителей обратно про-порциональны их условным эквивалентам.

Соотношение между величинами условных эквивалентов горячего и холодного теплоносителей определяет наклон температурных кривых на графиках изменения температур. Например, если W₁ = 2W₂, то изменение температуры холодного теплоносителя будет вдвое больше изменения температуры горячего теплоносителя.

На рис. 6.5 показаны характерные кривые изменения температур теплоносителей при движении их вдоль поверхности нагрева площадью F в зависимости от соотношения W₁/W₂ для прямотока и противотока.

Рассмотрим теперь уравнение теплопередачи. При выводе основного уравнения теплопередачи (5.1):

Q = kF(Т_ж1 – Т_ж2) = kF∆Т_ж (6.4)

принималось, что температуры горячего Т_ж1 и холодного Т_ж2 теплоносителей при передаче тепла через твердую стенку не изменяются. В действительности по всей длине теплообменника происходит передача теплоты от греющей жидкости к нагреваемой, в результате изменяются температуры обеих жидкостей по длине каналов, причем, как видно из рис. 6.1, на изменение температур большое влияние оказывают схема движения теплоносителей и величины условных эквивалентов.

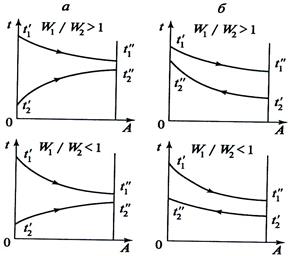
Рис. 6.5. Изменение температур теплоносителей при различных

схемах их движения: а – прямоток; б – противоток

Поэтому для теплообменного аппарата уравнение теплопередачи (5.1) приобретет вид:

_F

Q = ∫ k∆ТdF = kF∆Т_cр, (6.5)

⁰

где k – средний коэффициент теплопередачи;

F – площадь поверхности нагрева теплообменного аппарата;

∆Т_cр – средняя разность температур греющей и нагреваемой жидкости.

На основании несложных математических операций можно получить значение средней разности температур в виде:

∆Т_cр = ( ∆Т_б - ∆Т_м)/ln (∆Т_б/∆Т_м), (6.6)

где ∆Т_б и ∆Т_м - больший и меньший температурные напоры между рабочими жидкостями (разности температур теплоносителей на входе в теплообменник и выходе из него) вне зависимости от схемы движения жидкости (прямоток или противоток).

Для теплообменных аппаратов с прямотоком

∆Т_б = Т'₁ - Т'₂; ∆Т_м = Т"₁ - Т"₂. (6.7)

Для теплообменных аппаратов с противотоком

∆Т_б = Т'₁- Т"₂; ∆Т_м = Т"₁- Т'₂. (6.8)

Величину ∆Т_cр называют средним логарифмическим температур-ным напором.

Если температура одного из теплоносителей в пределах поверхности теплообмена остается постоянной (рис. 6.6) и равной температуре Т_s фазового превращения (испарения или конденсации), то средний логарифмический температурный напор определится по формуле:

∆Т_cр = (Т' - Т_s) / ln [(Т' - Т_s) /(Т" - Т_s), (6.9)

где Т' и Т" – температуры теплоносителя без фазового превращения на входе в теплообменный аппарат и выходе из него .

При ∆Т_б/∆Т_м < 1,7 величины ∆Т_б и ∆Т_м незначительно отличаются друг от друга. Поэтому вместо выражения (6.6) можно воспользоваться формулой среднеарифметического температурного напора:

∆Т_cр = 0,5(∆Т_б + ∆Т_м). (6.10)

В этом случае разница между среднелогарифмическим и среднеариф-метическим температурными напорами не превысит 3%.

Определение среднего температурного напора для теплообменников с перекрестным током и другими более сложными схемами движения теплоносителей производят по следующей формуле:

∆Т_cр = ∆Т_{cр.прот.}ε_∆Т , (6.11)

где ∆Т_{cр.прот.} - средний логарифмический температурный напор – опре-

деляют , как для теплообменника с противотоком, по фор-

муле (6.6);

ε_∆Т - поправочный коэффициент, меньший единицы, зависящий

от двух вспомогательных величин:

P = (Т"₂- Т'₂)/(Т'₁ – Т'₂) = ∆Т₂/∆Т; (6.12)

R = ( Т'₁ - Т"₁)/(Т"₂- Т'₂) = ∆Т₁/∆Т₂. (6.13)

Зависимости ε_∆Т = f (P,R) рассчитаны для различных схем движения теплоносителей и приводятся в справочной литературе.

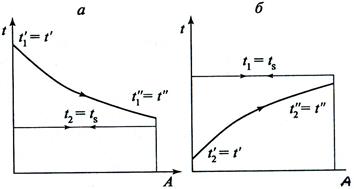
Рис. 6.6.Изменение температур теплоносителей при фазовых

превращениях: а – испарение; б - конденсация

Выше уже отмечалось, что противоточная схема является наиболее эффективной по сравнению с другими схемами. Критерием для оценки эффективности служит значение среднего температурного напора ∆Т_cр (6.6); в противоточной схеме он оказывается больше, чем в прямо-точной. Следовательно, рабочая поверхность теплообменника с проти-воточной схемой движения теплоносителя будет меньше, чем с прямоточной. Значит, при прочих равных условиях он будет наиболее компактным, а затраты материала на его изготовление – наименьшими. Кроме того, при осуществлении противотока можно получить более высокую конечную температуру Т"₂ для нагреваемой жидкости, чем при прямотоке; Т"₂ может стать даже выше температуры Т"₁ греющей жидкости на выходе, что в прямоточной схеме невозможно.

Следует заметить, что противоточная схема движения теплоносите-лей не всегда имеет существенные преимущества перед прямоточной. Так, расчеты показывают, что при большой разнице между условными эквивалентами греющего и нагреваемого теплоносителей (W₁/W₂ < 0,05 или W₁/W₂ > 10) и при kF/W₁ → 0 обе схемы становятся равноценными. Первое условие равнозначно несущественному изменению температуры одного из теплоносителей (например, при изменении его агрегатного состояния – кипение или конденсация). Второе условие означает, что средний температурный напор значительно превышает изменение температуры одного из теплоносителей.

При сравнении противоточной и перекрестной схем движения теплоносителей необходимо принять во внимание не только изменение величины среднего температурного напора, но и изменение условий теплообмена. При одинаковом гидравлическом сопротивлении и условии Nu /Pr^0,4 < 58 поперечное обтекание позволяет получить бо'льшую величину коэффициента теплоотдачи, чем продольное обтекание труб. Поэтому возможны такие условия, при которых теплообменник с перекрестным током при прочих равных условиях будет иметь меньшую поверхность теплообмена.

При конструктивном расчете должны быть известны расход теплоносителей, их температуры на входе Т'₁, Т'₂ и выходе Т"₁, Т"₂ и теплоемкости; искомая величина - рабочая поверхность теплообменного аппарата.

Массовый расход (кг/с) определяется по формуле:

m = wА_пρ, (6.14)

где w – средняя скорость теплоносителя, м/с;

А_п – площадь поперечного (живого) сечения канала, м/с;

ρ – плотность теплоносителя, кг/м³.

Рабочая поверхность теплообменного аппарата определяется из уравне-ния теплопередачи (6.5):

F = Q/(k ∆Т_cр). (6.15)

Если тепловой поток неизвестен, он определяется из уравнения (6.1).

Средний коэффициент теплопередачи определяется обычно по формулам плоской стенки, так как трубки теплообменника имеют небольшую толщину:

k = 1/(1/α₁ + δ/λ + 1/α₂), (6.16)

причем коэффициенты теплоотдачи греющего газа к стенке α₁ и от стенки к нагреваемой среде α₂ учитывают суммарное действие и конвекции и излучения, если, конечно, газовые среды способны излу-чать и поглощать тепловую энергию.

Коэффициенты теплоотдачи α₁ и α₂ вычисляют по среднеарифмети-ческим температурам соответствующих потоков.

Недостающая конечная температура Т"₁ греющего теплоносителя может быть найдена из уравнения теплового баланса (6.1).

Так получают исходные данные для определения общей поверхности нагрева F. Затем выбирают диаметры d труб по ГОСТу, а также задают оптимальные скорости теплоносителей. Определив по формуле (6.15) поверхность нагрева, скомпонованного из труб теплообменного аппарата, подсчитывают число труб n и их длину ℓ по формуле:

F = πdℓn. (6.17)

При проверочных расчетах теплообменников, когда известны их поверхность нагрева и ее конструктивные характеристики, а также расходы теплоносителей и их начальные параметры, определению подлежат конечные температуры теплоносителей.

Оптимальным теплообменником является аппарат, в котором процесс передачи теплоты удовлетворяет условию существования экстремума выбранного критерия оптимальности. В качестве критериев оптимизации могут быть выбраны технологические, конструктивные, термодинамические или технико-экономические показатели.