Пространственно-некогерентное объединение обнаруженных отметок и единичных замеров при централизованной обработке.

Полагаем, что МП РЛС – это несколько разнесенных в пространстве РЛС, работающих независимо друг от друга в общей зоне действия и их единичные замеры объединяются при совместной обработке. Такие системы могут создаваться на основе действующих однопозиционных РЛС.

Наиболее простым способом мультирадарной (третичной) обработки является «мозаичный», практический вариант которого состоит в разделении зоны ответственности на отдельные непересекающиеся области (домены), где используются данные, полученные от одной РЛС, а другие игнорируются. В каждом домене предпочтение отдается радиолокатору с лучшими характеристиками обнаружения. Недостатком метода является отказ от совместной обработке координатной информации в зонах перекрытия. Кроме того, при переходе воздушного судна из одного домена в другой возникает проблема идентификации траекторий.

Совместную обработку можно разбить на три этапа:

1. Упорядочение по пространству и времени (приведение к единой системе координат и единому времени отсчета).

2. Отождествление отметок по преобразованным отметкам.

3. Построение траекторий.

На различных позициях РЛС определяют местоположение целей относительно своих точек расположения. Следовательно, в центр обработки поступят координаты, различные по одной и той же цели. Необходимо привести их к одной системе и определить местоположение цели относительно центра обработки. В качестве единой системы координат может быть принята геодезическая система (долгота, широта, высота над уровнем моря). В ней в полной мере учитывается фактор кривизны земной поверхности, однако расчеты в такой системе сложны и их можно применять в тех случаях, когда расстояния между РЛС велики.

Когда расстояния между РЛС невелики, пользуются декартовой системой координат, начало которой привязывается к центру обработки информации, с поправкой по высоте. Расчеты в такой системе упрощаются, а ошибки, обусловленные заменой сферы плоскостью, приемлемы. Центр обработки находится в центре координат. Местоположение РЛС обозначено точкой О₁ и оно известно (рис.10.17).

Алгоритм пересчета координат следующий.

;

;

,

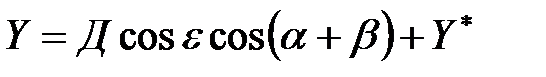где X, Y, H – координаты цели в единой системе координат;

X^*, Y^* – координаты точки стояния РЛС относительно центра обработки;

Д, b, e – координаты цели в полярной системе координат (дальность наклонная, азимут, угол места);

R_Э – эквивалентный радиус Земли;

a – угол сближения меридианов на широте пункта обработки.

Измерительная информация от разных позиций, относящаяся к одной и той же цели, поступает в различное время, поэтому ее необходимо привязать к единой шкале времени и преобразовать поток нерегулярно поступающих от разных позиций единичных замеров в регулярный поток. Приведение к единому времени отсчета необходимо для того, чтобы определить положение цели на какой-то один момент времени, что упрощает отождествление отметок. Процесс упорядочения измерительной информации во времени поясняется с помощью рис.10.18.

Три потока измеренных значений параметра a(t) от трех РЛС поступают нерегулярно во времени с периодами T_n1, T_n2, T_n3. Фиксируя значение a_i на весь период повторения до следующего единичного замера a_i+1 и осуществляя выборку из таких продолженных потоков одновременно и строго периодически (с периодом T_n), можно сформировать регулярные потоки единичных замеров.

Рассмотрим следующий пример. На обработку поступили две отметки А и Б с различным временем локации t_A и t_Б. Возможно, что эти отметки от одной и той же цели, зафиксированные в различные моменты времени. Вычисляется их положение на одно и то же время. Если они окажутся близко одна от другой, то вполне вероятно, что они относятся к одной цели (рис.10.19).

Приведение к единому времени осуществляется следующим образом.

1. Назначается время t, к которому приводятся отметки (в примере приводятся отметки к времени t = t_А).

2. Находится разность времени между отметками

.

3. Производится экстраполяция положения отметки Б на время Dt (определяется положение отметки Б на момент времени t = t_А), путем вычисления расстояния DS

.

Если Dt отрицательно, отметку перемещают в направлении, противоположном движению цели, в противном случае – по ходу движения. В результате получается взаимное расположение отметок по состоянию на один момент времени.

При одновременном наблюдении нескольких целей в МП РЛС возникает задача определения принадлежности полученных от различных позиций отметок определенным целям для исключения перепутывания. Задача может быть решена при межпозиционном отождествлении в МП РЛС с пространственно-когерентным объединением на уровне сигналов. В процессе отождествления устанавливается:

· сколько целей имеется в действительности, если отметки поступают от различных РЛС;

· как распределяются отметки по целям.

Основой решения задач отождествления является пространственное подобие первичной РЛИ об одной цели от разных источников, обусловленное фактическим наличием цели в определенной точке пространства. В качестве операций отождествления может быть использование стробирования пространства по координатам и параметрам движения цели. Если, например, измерены координаты по некоторой цели на одной позиции, то можно с учетом допустимых ошибок измерения сформировать стробы по соответствующим координатам в других позициях. Если обнаруженные отметки в стробы не попадают, они отбрасываются как ложные. Таким образом реализуется операция сравнения компонентов отметок от различных источников. При полном совпадении компонентов отметки считаются принадлежащими одной и той же цели. Однако в действительности из-за ошибок измерения и пересчета к единой системе координат и единому времени отсчета полного совпадения отметок не будет. Возникают две гипотезы:

1. Несовпадение произошло из-за ошибок в отметках, хотя они от одной и той же цели.

2. Несовпадение произошло потому, что отметки от разных целей.

Стробирование и разрешает эти гипотезы.

Если в результате проведенного сравнения установлено, что отметки принадлежат обнаруженным целям, необходимо осуществить распределение отметок по целям. При этом необходимо следовать следующим правилам. Во-первых, если отметки в области допустимых отклонений получены от одной и той же РЛС, то число целей равно числу отметок. Во-вторых, если от каждой из РЛС получено по равному числу отметок, то число целей равно числу отметок от одной РЛС. Распределение отметок по целям производится путем выбора наиболее правдоподобного варианта (рис.10.20). Вариант III исключается, так как по одной цели одна РЛС не может выдать одновременно две отметки. На рис.10.20 приведен пример для ситуации, когда две РЛС наблюдают две цели.

Для выбора варианта I или II можно воспользоваться методом минимума суммы квадратов расстояний. Для этого выполняются следующие операции.

1. Вычисляются расстояния между отметками (S₁, S₂, S₃, S₄).

2. Определяются суммы квадратов расстояний для каждого варианта:

.

3. Выбирается тот вариант, для которого сумма имеет наименьшее значение.

Такой алгоритм не является единственным. Пример решения задачи отождествления от пяти РЛС по четырем целям путем стробирования двумерного пространства по оценкам и ожидаемым ошибкам РЛС-1 показан на рис.10. 21.

Для отсева ложных гипотез целесообразно максимально использовать априорные сведения о возможных значениях скорости и ускорения целей, а также сигнальную информацию, получаемую в процессе наблюдения.

В результате отождествления определены отметки, относящиеся к тем или иным целям. Следующим этапом обработки следует объединение отметок от разных РЛС. Из теории ошибок известно, что если отдельные значения a_i величины a (от разных РЛС) получены с раздельной степенью точности, характеризуемой средней квадратической ошибкой s_i, то наиболее вероятным значением величины a является среднее взвешенное

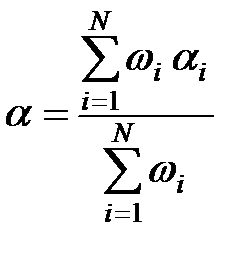, (10.16)

где 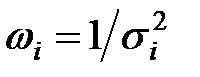– весовые коэффициенты, обратно пропорциональные квадратам соответствующих средних квадратических ошибок.

Если считать единичные замеры от разных РЛС a_i статистически независимыми, результирующая дисперсия среднего взвешенного определяется следующим образом

. (10.17)

В частном случае одинаковых ошибок единичных замеров

.

При наличии в системе МП РЛС одной высокоточной РЛС с минимальной ошибкой измерения наиболее вероятным значением величины a следует считать единичный замер, полученный этой i-ой РЛС , причем ошибка измерения определяется ошибкой этого единичного измерения 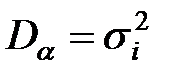. Можно считать отбор единичных точных замеров разновидностью весового объединения, когда вес остальных замеров равен нулю.

После пространственного объединения единичных замеров осуществляется построение траекторий с последующим их объединением. Одним из способов объединения траекторий является пространственно-некогерентное объединение. Такое объединение имеет следующие достоинства.

1. Обеспечивается полная децентрализация вторичной обработки. При этом распределяется нагрузка между вычислительными средствами.

2. Снижаются требования к пропускной способности линий передачи данных, так как передается не «сырая» информация, а сглаженные оценки параметров траекторий.

Применяются следующие способы объединения траекторий:

· отбор траекторий;

· весовое объединение траекторий.

Простейший способ объединения траекторий – отбор для каждой цели и в каждый момент времени «местной» траектории, построенной в какой-либо одной позиции. Такой способ называют еще как «мозаичный», практический вариант которого состоит в разведении зоны ответственности на отдельные непересекающиеся области (домены), где используются данные, полученные от одной определенной РЛС, а другие игнорируются. Выбор траектории осуществляется на основе определенной иерархии позиций, устанавливаемой центром совместной обработки. При такой обработке может теряться значительная часть информации, получаемой МП РЛС в целом. Недостатком метода является отказ от совместной обработки координат в зонах перекрытия. Кроме того, при переходе от траектории, формируемой одной позицией МП РЛС, к траектории, формируемой другой позицией, могут возникать скачки в результирующей траектории.

Более высокое качество дает весовое объединение траекторий, требующее больших вычислительных затрат. Простейший пример весового объединения – равновесное объединение N траекторий, когда дисперсия ошибки результата объединения уменьшается в N раз.