Функция неопределенности фазокодоманипулированного сигнала

Объем тела неопределенности всегда равен 4Е². Из этого следует, что идеальное тело неопределенности имеет вид перевернутой кнопки,

его основной объем сосредоточен в широком основании. Пик в точке τ=0, f_д=0 узкий в обеих плоскостях, что обеспечивает хорошее разрешение по времени и частоте. Вид такой функции неопределенности изображен на рис.4.175.

Подобной функцией неопределенности обладает реализация белого шума. В радиотехнических системах широкое применение нашли ФКМ сигналы, функция корреляции которых при удачном коде фазы приближается к идеальной. Самый лучший бинарный код – код Баркера. При его использовании уровень боковых лепестков функции неопределенности по дальности равен 1/N. Коды Баркера существуют для N=3,4,5,7,13.

С помощью согласованных фильтров производится сжатие сигналов во времени. Коэффициент сжатия равен базе сигнала

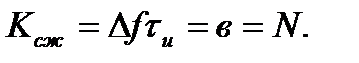(.4.99)

На рис.4.176 изображенафункция неопределенности по дальности ФКМ – сигнала с кодом Баркера, N=5.

Так как базы Баркера существуют только для 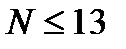, то коэффициент сжатия может оказаться недостаточным. Применяют другие коды, среди которых наиболее распространены M – последовательности (коды максимальной длины).

В этих кодах чередование нулей и единиц обладает свойствами случайной последовательности, поэтому соответствующие сигналы называют шумоподобными. М – последовательность может быть реализована с помощью схемы, изображенной на рис.4.177.

Число триггерных ячеек n называется основанием кода. Наибольшее число, которое может быть представлено n – разрядным двоичным кодом, равно 2ⁿ. Длина М – последовательности

N=2ⁿ-1. Вид кода зависит от того, к каким ячейкам подключен сумматор по модулю 2. Полученный код используется для фазовой манипуляции (рис.4.178).

Выбором достаточно большого N обеспечивают необходимое значение коэффициента сжатия и уровня боковых лепестков функции неопределенности.