Равновесие жидкости в поле земного тяготения
В качестве объемной силы в поле земного тяготения выступает сила тяжести. Полное ускорение объемных сил равно ускорению свободного падения g = 9,81 м/c2.
В выбранной системе координат проекции единичной объемной силы на оси Ox, Oy и Oz будут следующими:
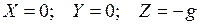 .
.
Знак «минус» в ускорении свободного падения соответствует направлению силы тяжести в отрицательную сторону оси Oz.
Подставляя значения X, Y, Z в уравнение поверхности уровня, получим
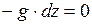
и следовательно,
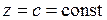 ,
,
где с – произвольная постоянная.
Таким образом, поверхностью уровня (поверхность равного давления) в однородной покоящейся жидкости будет любая горизонтальная плоскость, в том числе и свободная поверхность, независимо от формы сосуда или водоема. Горизонтальной плоскостью будет также граница раздела двух несмешивающихся жидкостей (рисунок 2.4).
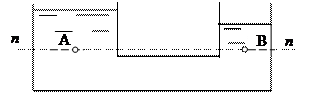
Рисунок 2.4 – Поверхность равного давления
Давление в точке А равно давлению в точке В, так как обе точки лежат на одной и той же поверхности уровня (поверхности равного давления).
2.5Основное уравнение гидростатики
Рассмотрим случай равновесия жидкости, когда на неё действует одна сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объёма жидкости. Пусть жидкость находится в сосуде (рисунок 2.5) и на её свободную поверхность действует давление р0. Найдём гидростатическое давление р в произвольно взятой точке М, расположенной на глубине h.
Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объём высотой h. Рассмотрим условия равновесия указанного объёма жидкости, выделенного из общего объёма. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объёма, т.е. вверх.
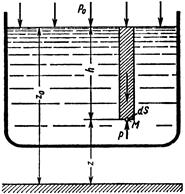
Рисунок 2.5 – Схема для вывода основного уравнения гидростатики
Запишем сумму сил, действующих на рассматриваемый объём в проекции на вертикаль
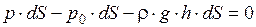 .
.
Последний член уравнения представляет собой вес жидкости в указанном объёме. Сократив выражение на dS и перегруппировав члены, найдём
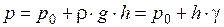
Полученное уравнение называют основным уравнением гидростатики; по нему можно подсчитывать давление в любой точке покоящейся жидкости.
2.6Абсолютное и избыточное давления. Вакуум
Рассмотрим случай, когда давление в сосуде р0 > ратм. Простейшим прибором жидкостного типа для измерения величины гидростатического давления является пьезометр, который представляет собой стеклянную трубку небольшого диаметра, открытую с одного конца и вторым концом присоединенную к сосуду, в котором необходимо измерить давление (рисунок 2.7).
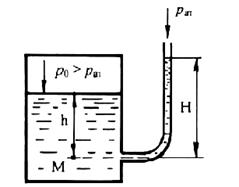
Рисунок 2.7 – Схема к определению избыточного давления
Давление р0, определенное с учетом атмосферного давления, называется абсолютным давлением 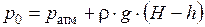 .
.
Давление р0, действующее на свободной поверхности жидкости в сосуде, превышает атмосферное давление на величину 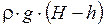 .Это давление называется избыточным давлением
.Это давление называется избыточным давлением
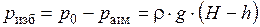
Недостаток до атмосферного давления называется вакуумметрическим давлением
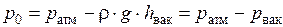 или
или 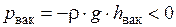 .
.
Взаимосвязь между абсолютным, избыточным и вакуумметрическим давлением изображена на рисунке 2.8.
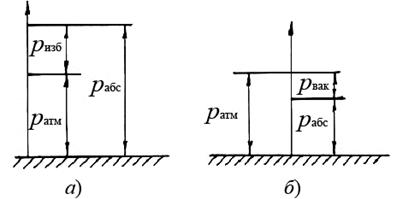
Рисунок 2.8 - Взаимосвязь между давлением:
а) – абсолютным и избыточным; б) абсолютным и вакуумметрическим
2.7Приборы для измерения давления
Для измерения давления жидкости или газа применяются различные приборы:
ü манометры — для измерения избыточного (или манометрического) давления,
ü вакуумметры — для измерения вакуума,
ü дифференциальные манометры — для измерения разности (перепада) давлений в двух точках (например, в двух сосудах).
Эти приборы могут быть:
ü жидкостными,
ü пружинными,
ü поршневыми,
ü электрическими,
ü комбинированными.
Наиболее широкое распространение получили жидкостные и пружинные приборы.
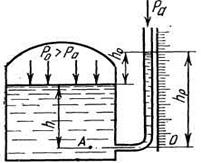
Рисунок 2.9 - Пьезометр
Жидкостный манометр (рисунок 2.9) — пьезометр представляет собой стеклянную трубку, нижний конец которой соединен с точкой, где измеряется давление, а верхний открыт и сообщается с атмосферой. Если давление на свободной поверхности жидкости в закрытом сосуде больше атмосферного, то уровень в пьезометрической трубке поднимется на высоту hр, называемую пьезометрической высотой. Ее измерение производится по установленной строго вертикально линейной шкале. Высоту столба жидкости в пьезометре hp можно найти из условия равновесия жидкости. Абсолютное давление в точке А (точка подключения пьезометра к сосуду) со стороны жидкости в пьезометре может быть выражено следующим образом
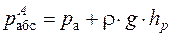
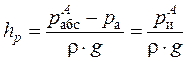
Таким образом, по высоте столба жидкости в пьезометре с открытым верхним концом можно определить величину избыточного давления в сосуде на уровне точки подключения.
Для точки A, находящейся под свободной поверхностью в сосуде на глубине h абсолютное давление равно
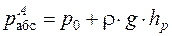
где р0 — давление на свободной поверхности в сосуде.
На основании второго свойства гидростатического давления в точке А давления со стороны жидкости в сосуде и в пьезометре равны. Тогда обозначив hp - h=h0 (рисунок 2.9), получим
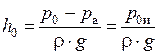 .
.
Из этого выражения следует, что разность высот уровней в пьезометре и сосуде характеризует избыточное давление на свободной поверхности жидкости в сосуде.
Если в сосуде абсолютное давление над свободной поверхностью будет равно атмосферному (сосуд открытый), то уровень в пьезометре установится на той же высоте, что и в сосуде, и hp=h. Это явление, называемое законом сообщающихся сосудов, используется для измерения уровня жидкости в сосудах при помощи уровнемеров или водомерных стекол.
Для измерения небольших давлений (не более 0,15...0,20 ати) применяются пьезометры, наполненные водой, для больших давлений, но не свыше 2,0...2,5 ати (0,2...0,25 МПа) — пьезометры, наполненные ртутью, так называемые ртутные манометры.
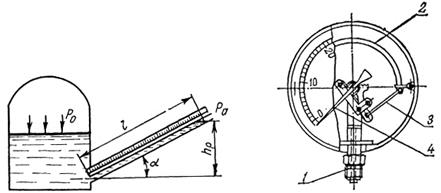
Рисунок 2.10 - Микроманометр с наклонной шкалой (а), пружинный манометр (б)
Для увеличения точности при измерении малых давлений используется наклонный микроманометр (рисунок 2.10, а). По его шкале вместо величины hp отсчитывается значительно большая величина 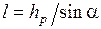 , что уменьшает относительную ошибку, возможную при измерении малых величин. Угол наклона манометрической трубки α можно изменять, при этом уменьшение угла наклона способствует увеличению точности измерений.
, что уменьшает относительную ошибку, возможную при измерении малых величин. Угол наклона манометрической трубки α можно изменять, при этом уменьшение угла наклона способствует увеличению точности измерений.
Для измерений значительных величин избыточных давлений в жидкостях или газах в практике используются металлические манометры. В пружинном манометре (рисунок 2.10, б) жидкость или газ поступает через штуцер 1 в изогнутую медную или стальную полую трубку-пружину 2. Под действием избыточного давления трубка-пружина стремится разогнуться. Движение ее конца при помощи пластинки 3 передается на зубчатку, приводящую в движение стрелку 4, отклонение которой показывает на шкале прибора величину избыточного (манометрического) давления.
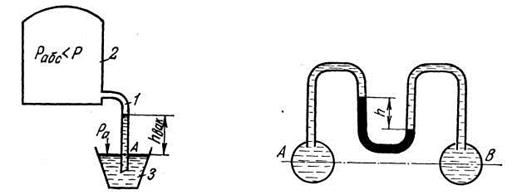
Рисунок 2.11 - Вакуумметр (а), дифференциальный U-образный манометр (б)
Для измерения вакуума применяется обратный пьезометр или вакуумметр (рисунок 2.11, а), представляющий собой трубку 1, соединенную с областью вакуума (сосуд 2). Нижний конец трубки опускается в сосуд 3, заполненный жидкостью, свободная поверхность которой находится под атмосферным давлением.
Для точки А, находящейся в жидкости в трубке 1 на уровне свободной поверхности в сосуде 3, можно записать, используя основное уравнение гидростатики и второе свойство гидростатического давления, следующее равенство
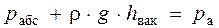
откуда следует, что вакуумметрическая высота, т. е. высота поднятия жидкости в вакуумметре (рисунок 2.11, а), составит
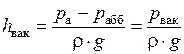 .
.
Для измерения вакуума применяются и металлические вакуумметры, устройство которых аналогично металлическим манометрам. Кроме того, в технике используются мановакуумметры — приборы, одна часть шкалы которых показывает манометрическое (избыточное) давление, а другая — вакуум.
Для измерения перепада (разности) давлений в двух точках используются дифференциальные манометры, простейшим из которых является U-образный манометр (рисунок 2.11, б). Разность давлений Δр в сосудах А и В с одной и той же жидкостью (плотностью ρ), находящихся на одинаковой высоте (или в двух трубопроводах, а также в двух сечениях одного трубопровода, отстоящих друг от друга на некотором расстоянии), определяется по разности уровней h рабочей жидкости (плотностью ρр) в обоих коленах дифманометра и вычисляется по зависимости
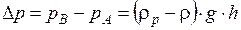
При больших разностях давлений в качестве рабочей жидкости применяется ртуть, при небольших — масло, спирт и др.
2.8Силы давления жидкости на плоскую стенку
Используем основное уравнение гидростатики для определения полной силы давления жидкости на плоскую стенку, наклонную к горизонту под некоторым углом α (рисунок 2.12). Вычислим силу F, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.
Выразим элементарную силу давления, приложенную к бесконечно малой площадке dS
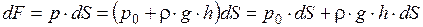 ,
,
где р0 - давление на свободной поверхности; h - глубина расположения площадки dS.
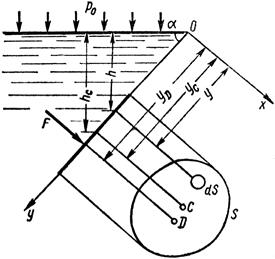
Рисунок 2.12 – Схема для определения силы давления жидкости на плоскую стенку
Для получения полной силы F проинтегрируем полученное выражение по всей площади S
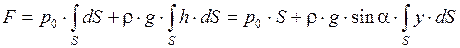 ,
,
где y- координата площадки dS.
Последний интеграл представляет собой статический момент площадки S относительно оси OX и равен произведению этой площади на координату её центра тяжести (точка C), т.е.
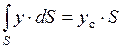 ,
,
где 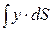 - статический момент площади S относительно линии пересечения свободной поверхности жидкости с плоскостью стенки (OX).
- статический момент площади S относительно линии пересечения свободной поверхности жидкости с плоскостью стенки (OX).
Следовательно
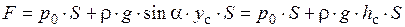 ,
,
где hc - глубина расположения центра тяжести площади S.
Или
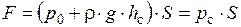 ,
,
Т.е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление pc в центре тяжести этой площади.
В общем случае давление р0 существенно отличается от атмосферного, поэтому полную силу давления можно найти как
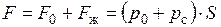 ,
,
где F0 - сила от внешнего давления;
Fж - сила давления от веса жидкости.
Положение центра давления. Центр давления силы F0 будет совпадать с центром тяжести фигуры, т.к. поверхностное давление, передаваясь через жидкость, равномерно распределяется по рассматриваемой площадке.
Избыточное давление распределяется неравномерно по площадке фигуры, поэтому центр давления Fж будет лежать ниже центра тяжести.
Центр давления Fж 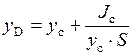 ,
,
где Jc - момент инерции площади S относительно центральной оси параллельной оси OX;
yс – координата центра тяжести фигуры.
Глубина погружения центра тяжести площади фигуры
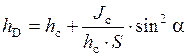 .
.
Равнодействующая сила (полная сила давления) является геометрической суммой сил F0 и Fж. Следовательно, точка приложения этой силы будет лежать между центром тяжести и центром давления точкой 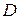 .
.
Дата добавления: 2016-11-29; просмотров: 2526;











