Основные физико-механические свойства жидкостей и газов

1.1 Основные физические свойства жидкостей

Рассмотрим физические свойства жидкостей, определяющие их поведение при гидравлических процессах и применение в различных областях техники.

К основным физическим свойствам жидкостей следует отнести те её свойства, которые определяют особенности поведения жидкости при её движении. Такими являются свойства, характеризующие концентрацию жидкости в пространстве, свойства, определяющие процессы деформации жидкости, определяющие величину внутреннего трения в жидкости при её движении, поверхностные эффекты.

1) Важнейшим физическим свойством жидкости, определяющим её концентрацию в пространстве, является плотность жидкости.

Рисунок 1.2 – К определению плотности

Выделим малый объём жидкости или газа 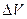(рисунок 1.2), окружающий точку М в момент времени t. Масса этого объёма будет .

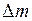Плотностью ρ (кг/м³) называют массу жидкости, заключённую в единице объёма; для однородной жидкости определяется по формуле

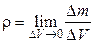, т.е. ,

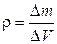где 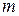– масса жидкости в объёме .

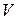Плотность характеризует инерционные свойства сплошной среды и в общем случае зависит от координат точки и времени

.

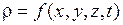Величины плотности реальных капельных жидкостей в стандартных условиях изменяются в системе единиц СИ в широких пределах от 700 кг/м ³ до 1800 кг/м ³. Плотность пресной воды равна 1000 кг/м³, солёной морской воды - 1020 ÷ 1030, нефти и нефтепродуктов – 650 ÷ 900 кг/м³, ртути – 13596 кг/м³.

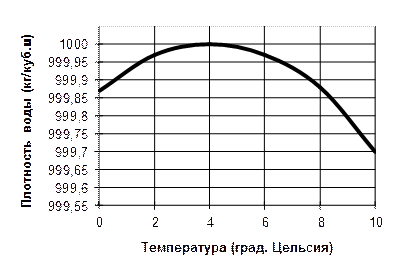
Рисунок 1.3 – Зависимость плотности от температуры

Плотность жидкости зависит от температуры и давления. Все жидкости, кроме воды, характеризуются уменьшением плотности с ростом температуры. Плотность воды имеет максимум при t = 4 ^оC и уменьшается при любых других температурах (рисунок 1.3). В этом проявляется одно из аномальных свойств воды. Температура, при которой плотность воды максимальная, с увеличением давления уменьшается. Так, при давлении 14 МПа вода имеет максимальную плотность при 0,6 ^оC.

При изменении давления плотность жидкостей изменяется незначительно. В большинстве случаев плотность жидкости в расчётах можно принимать постоянной. Однако встречаются случаи, когда изменением плотности пренебрегать нельзя, т.к. это может привести к значительным ошибкам.

Удельным весом 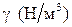называют вес единицы объёма жидкости, т.е.

.

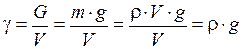Относительный вес (относительная плотность) жидкости. Иногда удобно использовать такую характеристику жидкости, которая называется «относительный удельный вес». Это отношение удельного веса жидкости к удельному весу пресной воды

,

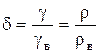где ρ _в = 1000 кг/м³ – плотность воды при 4^оС и давлении в 1 атм.

Единицы измерения: относительный удельный вес - величина безразмерная.

Если жидкость не однородна, то эти формулы определяют среднее значение удельного веса и плотности в данном объёме.

2) Сжимаемость – способность жидкости или газа под действием внешнего давления изменять свой объём а, следовательно, плотность.

Сжимаемость характеризуется коэффициентом β_р объёмного сжатия, который представляет собой относительное изменение объёма, приходящегося на единицу давления, т.е.

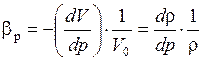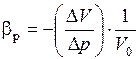или м²/Н (Па^-1).

Знак « – » в формуле обусловлен тем, что положительному приращению (увеличению) давления р соответствует отрицательное приращение (уменьшение) объёма .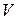

Рассматривая конкретные изменения 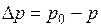и 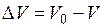, и считая β_р постоянным, получаем формулу для определения конечного объема при изменении давления

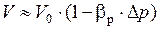м³,

или находим приближенную формулу для определения плотности

; ,

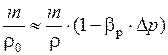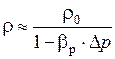где ρ и ρ₀ – плотности при давлени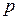и и .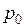

Капельные жидкости относятся к категории плохо сжимаемых тел, т.к. межмолекулярные расстояния в капельной жидкости малы и при деформации жидкости приходится преодолевать значительные силы отталкивания, действующие между молекулами, и даже испытывать влияние сил, действующих внутри атома. Тем не менее, сжимаемость жидкостей в 5 - 10 раз выше, чем сжимаемость твёрдых тел, т.е. можно считать, что все капельные жидкости обладают упругими свойствами.

Свойство, обратное сжимаемости называется упругостью среды. Характеризуется упругость объёмным модулем упругости Е, величиной обратной коэффициенту β_р объёмного сжатия

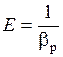Па, МПа.

Жидкость характеризуется низкой сжимаемостью, т.е. высокой упругостью:

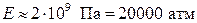– для воды, 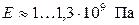– для нефти.

С упругостью среды связана важная характеристика – скорость звука в данной среде

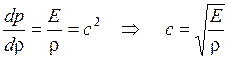м/с.

Следовательно, характеристикой сжимаемости в состоянии покоя служит скорость звука в данной среде: 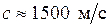- в воде, 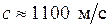- в нефти.

3) Температурное расширение – это свойство жидкостей изменять объем при изменении температуры; характеризуется температурным коэффициентом объемного расширения β_t, который представляет собой относительное изменение объёма (или плотности), при изменении температуры 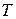на 1°С и постоянном давлении, т.е.

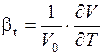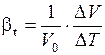или °С^-1.

Для большинства жидкостей коэффициент β_t с увеличением давления уменьшается (рисунок 1.4).

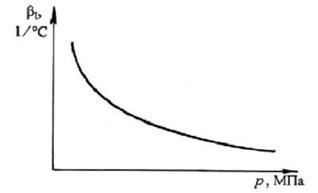
Рисунок 1.4 - Зависимость коэффициента объемного расширения β_t от давления р

Для воды с увеличением давления при температуре до 50 ºС коэффициент β_t растет, а при температуре выше 50 ºС уменьшается.

Для большинства жидкостей коэффициент b_t с увеличением давления уменьшается. Коэффициент b_t с уменьшением плотности нефтепродуктов от 920 до 700 кг/м³ увеличивается от 0,0006 до 0,0008; для рабочих жидкостей гидросистем b_t обычно принимают не зависящим от температуры. Для этих жидкостей увеличение давления от атмосферного до 60 МПа приводит к росту b_t примерно на 10 – 20 %. При этом, чем выше температура рабочей жидкости, тем больше увеличение b_t.

Рассматривая конечные приращения 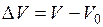и 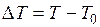, и принимая β_т постоянным, получаем формулу для определения конечного объема жидкости при изменении температуры

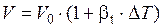м³.

Или находим приближенную формулу

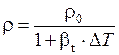кг/м³,

где ρ₀ и ρ - плотность при температурах 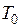и .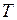

Т.е. β_t имеет малые значения, и можно считать, что плотность жидкости изменяется незначительно при небольшом изменении диапазона температур: 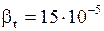- для воды при Т = 1°С и р = 1 атм.

4) Растворение газов -способность жидкости поглощать (растворять) газы, находящиеся в соприкосновении с ней. Все жидкости в той или иной степени поглощают и растворяют газы. Это свойство характеризуется коэффициентом растворимости k_р.

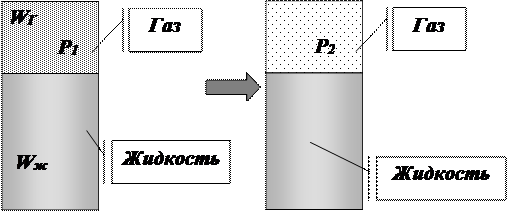
Рисунок 1.5 – Растворение газа в жидкостях

Относительное количество газа, которое может раствориться в жидкости до ее насыщения, прямо пропорционально давлению на поверхности раздела.

Если в закрытом сосуде (рисунок 1.5) жидкость находится в контакте с газом при давлении р₁, то газ начнёт растворяться в жидкости. Через какое-то время произойдёт насыщение жидкости газом и давление в сосуде изменится. Коэффициент растворимости связывает изменение давления в сосуде с объёмом растворённого газа и объёмом жидкости следующим соотношением

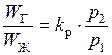
где W_Г – объём растворённого газа при нормальных условиях,

W_Ж – объём жидкости,

р₁ и р₂ – начальное и конечное давление газа.

Коэффициент растворимости зависит от типа жидкости, газа и температуры.

При температуре 20 ºС и атмосферном давлении в воде содержится около 1,6% растворенного воздуха по объему (k_p = 0,016). С увеличением температуры от 0 до 30 ºС коэффициент растворимости воздуха в воде уменьшается. Коэффициент растворимости воздуха в маслах при температуре 20 ºС равен примерно 0,08 – 0,1. Кислород отличается более высокой растворимостью, чем воздух, поэтому содержание кислорода в воздухе, растворенном в жидкости, примерно на 50% выше, чем в атмосферном. При уменьшении давления газ из жидкости выделяется. Процесс выделения газа протекает интенсивнее, чем растворение.

Наличие газа растворённого в жидкости может оказывать как благоприятное воздействие (снижается вязкость жидкости, плотность и т.д.), так и неблагоприятные факторы. Выделяющийся газ может оказаться не безопасным для окружающей среды, огнеопасным и взрывоопасным (углеводородный газ). Газ, растворённый в жидкости, как и газ в свободном состоянии может также способствовать коррозии стенок труб и оборудования, вызывать химические реакции, ведущие к образованию отложений твёрдых солей на стенках труб, накипей и др.

5) Кипение – способность жидкости переходить в газообразное состояние. Иначе это свойство жидкостей называют испаряемостью.

При понижении давления в жидкости происходит выделение растворенного в ней газа, который затем испаряется. Интенсивность процесса парообразования зависит от температуры кипения жидкости при нормальном атмосферном давлении: чем выше температура кипения жидкости, тем меньше её испаряемость. Характеристикой испаряемости является давление насыщенных паров р_н.п.: чем выше температура, тем больше давление насыщенного пара жидкости.

В результате понижения давления в жидкости до давления р_н.ппри определенной температуре в ней образуются пузырьки, заполненные парами жидкости и газа, которые выделились из жидкости. Кипение жидкости может возникнуть в результате понижения давления при существенно меньшей температуре кипения t = 100 °С. Такое кипение получило название «холодное кипение».

6) Поверхностное натяжение.

Когда мы говорим о жидкости как о сплошной среде, это вовсе не означает, что эта среда бесконечна и безгранична. Жидкое тело всегда имеет границы, это либо твёрдые стенки каналов, либо границы раздела с газообразной средой, либо это граница раздела между различными несмешивающимися жидкостями. Такие границы можно с полным правом называть естественными границами. В некоторых случаях границы могут выделяться условно внутри самой движущейся жидкости. На естественных границах в пограничном слое жидкости между молекулами самой жидкости и молекулами окружающей жидкость среды существуют силы притяжения, которые, в общем случае, могут оказаться не равными. В то же время силы взаимодействия между остальными молекулами жидкости, находящимися внутри объёма, ограниченного пограничным слоем взаимно уравновешены. Таким образом, остаются не уравновешеными силы взаимодействия между молекулами, находящимися лишь во внешнем (пограничном слое). Тогда в пограничном слое возникают напряжения, которые автоматически балансируют не сбалансированные силы притяжения. Такие напряжения называются поверхностным натяжением жидкости. Этому напряжению будут соответствовать силы поверхностного натяжения. Под действием этих сил малые объёмы жидкости принимают сферическую форму (форму капли), соответствующей минимуму внутренней энергии; в трубках малого диаметра жидкость поднимается (или опускается) на некоторую высоту по отношению к уровню покоящейся жидкости (рисунок 1.6).

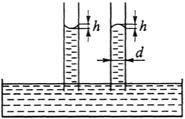
Рисунок 1.6 - Действие сил поверхностоного натяжения

Последнее явление носит название капиллярности: жидкость в трубке малого диаметра (капилляре) будет подниматься, если жидкость по отношению к стенке капилляра будет смачивающей жидкостью, и наоборот, будет опускаться, если жидкость для стенки капилляра окажется не смачивающей.

Высоту h подъёма (опускания) жидкости в капилляре с диаметром d можно определить из соотношения: ,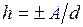

где А - постоянная зависящая от свойств жидкости.

Для воды 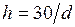, для ртути 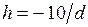мм.

Силы поверхностного натяжения малы и проявляются при малых объёмах жидкости. Величина напряжений на границе раздела зависит от температуры жидкости; при увеличении температуры внутренняя энергия молекул возрастает и, естественно, уменьшается напряжение в пограничном слое жидкости и, следовательно, уменьшаются силы поверхностного натяжения.

7)Вязкость жидкостей

При движении реальной жидкости она расходуют часть своей механической энергии на работу против сил внутреннего трения. Эти потери механической энергии носят название диссипации (потери) энергии и представляют собой необратимый переход кинетической энергии потока в тепловую энергию молекулярного движения.

Вязкостьпредставляет собой свойство жидкости сопротивляться сдвигу её слоёв и проявляется в результате её движения. Вязкость есть свойство противоположное текучести: более вязкие жидкости (глицерин, смазочные масла и т.д.) являются менее текучими, и наоборот.

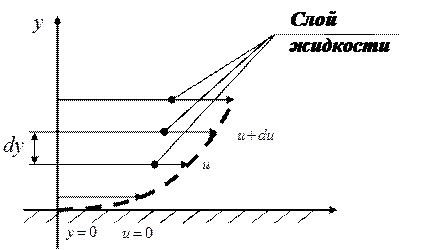
Рисунок 1.7 - Действие сил внутреннего трения

При течении вязкой жидкости вдоль твёрдой стенки происходит торможение потока, обусловленное вязкостью (рисунок 1.7). Скорость u уменьшается по мере уменьшения расстояния y от стенки вплоть до u =0 при y =0, а между слоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений, так называемых напряжений трения.

Напряжения, возникающие при деформации сдвига согласно гипотезе Ньютона пропорциональны градиенту скорости в движущихся слоях жидкости. Таким образом, закон жидкого трения Ньютона имеет вид

,

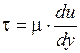где μ - коэффициент пропорциональности, получивший название динамической вязкости жидкости;

du - приращение скорости, соответствующее приращению координаты dу.

Поперечный градиент скорости 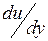определяет изменение скорости, приходящееся на единицу длины в направлении нормали к стенке и, следовательно, характеризует интенсивность сдвига жидкости в данной точке.

При постоянстве касательного напряжения по поверхности S полная касательная сила (сила трения), действующая на этой поверхности

.

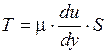Динамическая вязкость жидкости имеет размерность Пуаз:

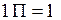дин·с/см² или .

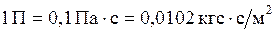Помимо динамического коэффициента вязкости используется кинематический коэффициент вязкости:

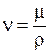, Ст

Кинематическая вязкость жидкости имеет размерность Стокс:

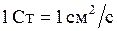= 10^-4 м²/с.

По своему физическому смыслу коэффициент вязкости представляет собой коэффициент переноса импульса в движущейся сплошной среде, а закон жидкого трения Ньютона представляет собой закон переноса импульса.

Коэффициент вязкости является физической характеристикой сплошной среды и для нормальных жидкостей и всех газов (так называемых ньютоновских сплошных сред) не зависит от кинематических характеристик движения (т.е. от распределения скоростей).

Вязкость капельной жидкости зависит от температуры и уменьшается с увеличением последней (рисунок 1.8, а). Вязкость газов, наоборот, с увеличением температуры возрастает. Объясняется это различием природы вязкости в жидкостях и газах. В жидкостях молекулы расположены гораздо ближе друг к другу, чем в газах, и вязкость вызывается силами молекулярного сцепления. Эти силы с увеличением температуры уменьшаются, поэтому вязкость падает. В газах же вязкость обусловлена беспорядочным тепловым движением молекул, интенсивность которого увеличивается с повышением температуры. Поэтому вязкость газов с увеличением температуры возрастает.

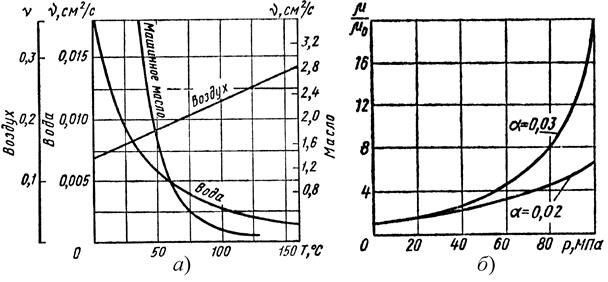
Рисунок 1.8 – Зависимости вязкости от температуры и давления

Влияние температуры на вязкость определяется формулой

,

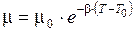где μ и μ₀ - вязкость при температуре Т и Т₀;

β – эмпирический коэффициент, значение которого для масел изменяется в пределах .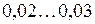

Вязкость жидкости зависит также от давления (рисунок 1.8, б), однако это проявляется при относительно больших значениях давления (более 20 30 МПа). С увеличением давления вязкость большинства жидкостей вырастает, и определяется формулой (законом Баруса)

,

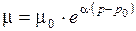где μ и μ₀ - вязкость при давлении р и р₀;

α – пьезокоэффициент вязкости, значение которого для минеральных масел изменяется в пределах 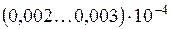1/МПа.

Вязкость минеральных масс при увеличении давления от 0 до 400атм приблизительно удваивается.

Вязкость жидкости измеряют при помощи вискозиметров. Наиболее распространенным является вискозиметр Энглера, который представляет собой цилиндрический сосуд диаметром 106 мм, с короткой трубкой диаметром 2,8 мм, встроенной в дно. Время t истечения 200 см³ испытуемой жидкости из вискозиметра через эту трубку под действием силы тяжести, деленной на время t_вод истечения того же объема дистиллированной воды при 20 °С выражает вязкость в градусах Энглера: 1°Е=t/t_вод , где t_вод = 51,6 с. Формула для пересчёта градусов Энглера в стоксы в случае минеральных масел

.

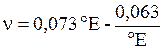1.5 Неньютоновские жидкости

Гидродинамические свойства сплошных сред определяются характером связи напряжения вязкого трения τ и кинематических характеристик течения, в частности – скорости сдвига .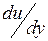

Функциональная зависимость 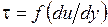называется реологическим уравнением сплошной среды.

Для широкого класса сплошных сред реологическим уравнением является закон жидкого трения Ньютона:

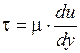
устанавливающий линейную зависимость 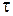от .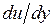

Сплошные среды, течение которых подчиняется линейному закону Ньютона, называются нормально-вязкими илиньютоновскими жидкостями.

К ньютоновским жидкостям относятся все газы, вода, спирты, эфиры, растворители, светлые нефтепродукты, незагущенные минеральные масла и т. д.

Графическое представление реологического уравнения (в координатах (τ, 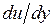)) называется реологической кривой или кривой течения (рис.1.9).

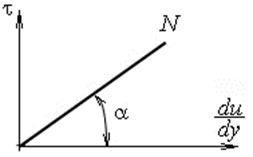
Рисунок 1.9 - Реологическая кривая ньютоновских жидкостей

Существует обширный класс жидкостей, течение которых не подчиняется линейному закону Ньютона. Такие жидкости называются аномальными или неньютовскими. Кривые течения неньютоновских жидкостей отличаются от прямых, проходящих через начало координат.

Неньютовские жидкости можно разделить на 3 класса:

1) неньютоновские вязкие жидкости (стационарно вязкие жидкости), для которых касательное напряжение зависит только от скорости сдвига ;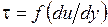

2) нестационарно вязкие жидкости, для которых связь τ с 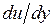зависит от времени действия напряжений .

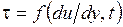3) вязкоупругие жидкости – среды, обладающие свойствами как упругого твёрдого тела, так и жидкости, а также способные к частичному восстановлению формы после снятия напряжений:

.

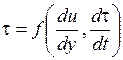Тема 2

Гидростатика

2.1 Понятие гидростатического давления

Гидростатика — это раздел гидравлики, изучающий жидкость в состоянии покоя. Она изучает законы равновесия жидкости и распределения в ней давления.

Одной из основных теоретических задач гидростатики является вопрос о характере распределения давления в объеме жидкости, которая в самом общем случае может находиться в абсолютном или относительном покое.

Абсолютный покой. Если жидкость находится в покое (скорость движения равна нулю, т.е. 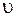=0) относительно системы координат, жестко связанной с Землей, такой покой называется абсолютным. Например, жидкость, находящаяся в покое в любом аппарате или емкости (резервуаре), которые в свою очередь находятся в неподвижном состоянии относительно Земли.

Относительный покой. Если жидкость находится в покое (скорость движения равна нулю, т.е. 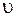=0) относительно системы координат, которая движется относительно Земли, такой покой называется относительным. Например, жидкость, находящаяся в покое в любом аппарате или емкости (резервуаре), которые свою очередь находятся в движении относительно Земли. При этом, движение может быть равноускоренным или с постоянной скоростью.

Когда жидкость находится в покое, то она характеризуется свойствами, очень близкими к свойствам идеальной жидкости. Вследствие текучести в жидкости действуют силы не сосредоточенные, а непрерывно распределённые по её объёму или поверхности.

На жидкость в состоянии покоя действуют следующие силы:

ü массовые силы, пропорциональны массе жидкости – это силы тяжести и инерции;

ü поверхностные силы (атмосферное давление, давление поршня или других предметов, находящихся на поверхности), которые непрерывно распределены по поверхности жидкости и при равномерном их распределении пропорциональны площади этой поверхности. Эти силы возникают из-за воздействия соседних объёмов жидкости или же воздействия других тел (твёрдых или газообразных), соприкасающихся с данной жидкостью.

Когда жидкость находится в равновесии, то под действием внешних сил в жидкости возникает давление. Давление в неподвижной жидкости называется гидростатическим давлением.

Рассмотрим некоторый объем жидкости массой М, находящийся в состоянии относительного покоя (рисунок 2.1).

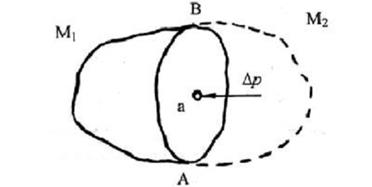
Рисунок 2.1 – Схема для определения гидростатического давления

Рассечем объем, занимаемый жидкостью, произвольной плоскостью АВ на две части, содержащие соответственно массы М1 и М2, и отбросим одну из них (например, правую). Чтобы сохранить равновесие оставшейся в левой части массы жидкости М1, необходимо приложить силу, эквивалентную действию отброшенной массы М2. Эта сила ∆F будет равномерно распределена по площади сечения ∆S. Тогда отношение 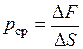представляющее собой среднюю силу, действующую на единицу площади ∆S, будет называться средним гидростатическим давлением.

В общем случае величина среднего давления р_ср будет тем меньше отличаться от истинного значения давления, например в точке а, чем меньше будет площадь сечения ∆S, т.е. истинное гидростатическое давление равно

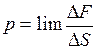
Сила, действующая на единицу площади ∆S при стремлении (стягивании) этой площади к размерам точки А, называется силой гидростатического давления.

За единицу давления принят Паскаль – давление, вызываемое силой 1Н, равномерно распределённой по нормальной к ней поверхности площадью 1 м².

В технике в настоящее время продолжают применять также систему единиц метр, килограмм-сила, секунда (МКГСС), в которой за единицу давления принимается 1кгс/ м². Широко используют также внесистемные единицы – техническую атмосферу и бар:

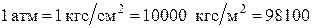Па; ; .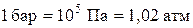

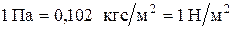Давление часто выражается высотой столба жидкости, которая называется пьезометрической высотой или пьезометрическим напоро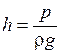м

, м.

Пьезометрическая высота – это высота такого столба жидкости, который своим весом способен создать давление, равное гидростатическому давлению в рассматриваемой точке.

;

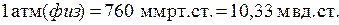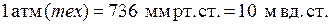
2.2Свойства гидростатического давления

Первое свойство: на внешней поверхности жидкости гидростатическое давление всегда направлено по нормали внутрь рассматриваемого объёма.

Действительно, если бы сила ∆F (рисунок 2.1) была направлена не по нормали к площадке ∆S, то эту силу можно было бы разложить на составляющие: нормальную и касательную к площадке ∆S. Из-за текучести жидкости касательная составляющая привела бы жидкость в движение, то есть в этом случае равновесие жидкости было бы невозможно. Поскольку жидкость не сопротивляется растягивающим усилиям, то сила ∆F может быть только сжимающей.

Таким образом, по любой поверхности, проведенной внутри покоящейся жидкости, всегда действует только распределенная сжимающая сила.

Второе свойство: состоит в том, что в любой точке внутри жидкости давление по всем направлениям одинаково. Иначе это свойство давления звучит так: на любую площадку внутри объёма жидкости, независимо от её угла наклона, действует одинаковое давление. Доказательство этого свойства сводится к определению равенства сил, действующих на боковые грани тетраэдра (рисунок 2.2), то есть

Р_х = Р_y = Р_z = Р_n.

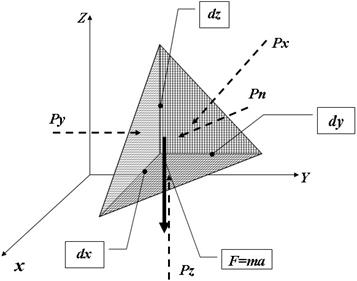
Рисунок 2.2 - Схема для доказательства свойства гидростатического давления

Доказательство этого равенства можно найти в любой учебной литературе по гидравлике.

Поверхность уровня

Поверхность, точки которой имеют одинаковые значения данной функции, называется поверхностью уровня (рисунок 2.3). К поверхности равного уровня относятся:

ü поверхности равного давления;

ü изотермические поверхности (поверхности равной температуры);

ü поверхности равной плотности и т.д.

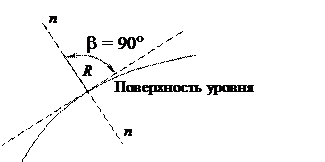
Рисунок 2.3 – Поверхность уровня

В гидравлике рассматриваются поверхности равного давления.

Принимая p = const (dp = 0) c учетом того, что для жидкости r ¹ 0 (см. рисунок 2.2), получим

.

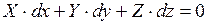Это уравнение является дифференциальным уравнением поверхности уровня (здесь X,Y,Z являются функциями координат).

Поверхности уровня обладают следующими свойствами:

Первое свойство поверхности уровня заключается в том, что две различные поверхности уровня не пересекаются между собой.

Докажем это от обратного.

Допустим, что поверхности уровня пересекаются. Тогда во всех точках линии пересечения этих поверхностей давление одновременно должно быть равно р₁ и р₂, что противоречит основной теореме гидростатики, в которой доказывается, что гидростатическое давление р одинаково по всем направлениям.Следовательно, две различные поверхности уровня не пересекаются.

Второе свойство – внешние массовые (объемные силы) направ­лены по нормали к поверхности уровня (см. рисунок 2.3).

Известно, что уравнение работы dA силы R на пути ds имеет вид

,

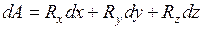где R_x, R_y и R_z – проекции силы по координатным осям Ox, Oy и Oz.

Но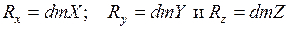

где dm – элементарная масса;

X, Y, Z – проекции ускорения силы R по тем же координатным осям.

Тогда

.

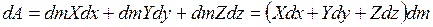Но для поверхности уровня

.

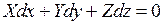Поэтому работа силы R(внешней объемной силы ) равна нулю. Следовательно, для поверхности уровня

,

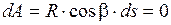где b = Ð(R,S).

Это возможно лишь при cosb = 0, т.е. внешняя сила должна быть нормальна к поверхности уровня (b = 90°).