Электрический ток. Необходимые условия существования тока.

Электрическим током называется любое упорядоченное движение электрических зарядов. Если в проводнике создать электрическое поле, то в нем свободные электрические заряды придут в движение – возникает ток, называемый током проводимости. Если в пространстве перемещается заряженное тело, то ток называется конвекционным. За направление тока принимается направление движения положительно заряженных частиц.

Для возникновения и существования тока необходимо с одной стороны, наличие свободных заряженных частиц, а с другой – наличие электрического поля в проводнике. Количественной характеристикой служит величина I называемая силой тока и определяемая зарядом, протекающим через поперечное сечение проводника в единицу времени,

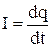. 4.1

Сила тока величина скалярная, измеряется в амперах.

Электрический ток может быть распределен по поверхности, сквозь которую он протекает, неравномерно. Более детально ток можно характеризовать с помощью вектора плотности тока 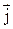. Он численно равен силе тока, протекающей через единичную площадку, перпендикулярную к направлению движения зарядов

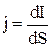. 4.2

Зная вектор плотности тока в каждой точке поверхности можно найти силу тока через эту поверхность

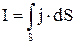. 4.3

Пусть заряд свободной частицы равен 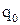, концентрация свободных зарядов равна n, скорость их упорядоченного движения 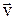. Тогда за время 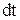через поперечное сечение проводника будет переноситься заряд 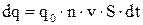. Учитывая 4.1 и 4.2, для плотности тока получим выражение:

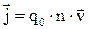. 4.4

Так как скорость 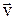является вектором, то и плотность тока также будет вектором.

2.4.3. Закон Ома для участка цепи. Дифференциальная форма закона Ома.

Г. Ом на опыте установил, что сила тока в однородном проводнике прямо пропорциональна приложенному напряжению и обратно пропорциональна его сопротивлению

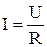. 4.5

Величина R называется электрическим сопротивлением проводника и зависит от его геометрических размеров, свойств материала, из которого он изготовлен и температуры

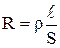, 4.6

где 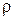- удельное сопротивление, величина численно равная сопротивлению куба вещества с ребром 1 м, при условии, что ток течет в направлении перпендикулярном граням куба.

Закон Ома можно записать в дифференциальной форме. Рассмотрим цилиндрический проводник длиной 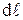и площадью поперечного сечения 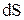. Напряжение приложенное к проводнику 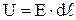, где Е – напряженность поля в проводнике. Наконец, сопротивление проводника по 4.6 равно 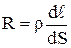. Подставляя эти значения в 4.5, получим

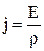. 4.7

Носители заряда движутся в направлении вектора Е и поэтому направление векторов 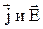совпадают. Таким образом, окончательно, можно получить:

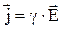, 4.8

где 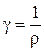- удельная проводимость вещества.

Формула 4.8 выражает закон Ома в дифференциальной форме.

3.4.3. Источники тока. Сторонние силы. ЭДС источника тока.

Если два разноименно заряженных тела соединить проводником, то в нем возникает электрический ток. Возникновение тока приводит к тому, что поле очень быстро исчезает и, следовательно, ток прекращается. Для того, чтобы поддерживать ток достаточно длительное время нужно от тела с меньшим потенциалом непрерывно отводить приносимые заряды, а к телу с большим потенциалом непрерывно их подводить. Иными словами электрическая цепь должна быть замкнутой. Но электрическое поле не может перемещать заряды по замкнутому пути и поэтому наряду с электрическими силами на перемещающиеся заряды должны действовать и силы не электростатического характера, так называемые сторонние силы.

Величину равную работе сторонних сил по перемещению единичного положительного заряда называют электродвижущей силой источника (ЭДС)

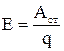. 4.9

По аналогии с электрическими силами стороннюю силу можно представить в виде:

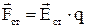, 4.10

где 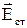- напряженность поля сторонних сил.

Тогда 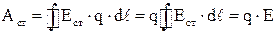и, следовательно,

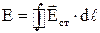. 4.11

Рассмотрим неоднородный участок цепи 1 – 2 (рис.22). На участке 1-2 на заряды будут действовать две силы: электрическая сила 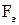и сторонняя сила 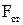и их результирующая 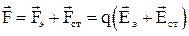. Тогда работа по перемещению заряда между точками 1 и 2 будет определяться по формуле:

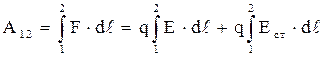. 4.12

Но 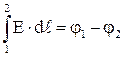, а 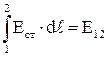, и тогда 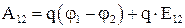. 4.13

Величину 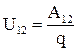называют напряжением между двумя точками электрической цепи

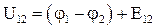. 4.14

При отсутствии источника тока 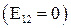напряжение 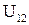совпадает с разностью потенциалов.

4.4.3. Работа и мощность постоянного тока. Закон Джоуля - Ленца.

При упорядоченном перемещении электрических зарядов электрическое поле совершает работу 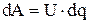. Из 4.1 найдем, что 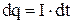и тогда 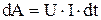. После интегрирования можно получить

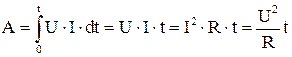. 4.15

Следовательно, для мощности тока получим:

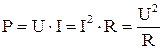. 4.16

При прохождении тока по проводнику он нагревается. Джоуль и Ленц установили, что количество теплоты, выделяющееся в проводнике, может быть найдено по формуле:

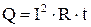. 4.17

Если сила тока изменяется во времени, то закон Джоуля-Ленца можно записать в виде:

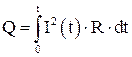. 4.18

Закон Джоуля – Ленца можно записать в дифференциальной форме. Выделим в проводнике с током I элементарный объем в форме цилиндра длиной 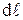и площадью поперечного сечения 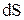. Согласно закону Джоуля – Ленца 4.17 в нем будет выделяться количество теплоты:

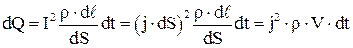. 4.19

Количество теплоты, отнесенное к единице объема и единице времени, называется удельной тепловой мощностью тока

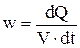. 4.20

Учитывая 4.19 выражение 4.20 примет вид

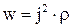. 4.21

Воспользовавшись соотношением 4.8 выражение 4.21 можно записать в виде:

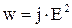. 4.22

Формулы 4.21 и 4.22 выражают закон Джоуля – Ленца в дифференциальной форме.