ГЛАВА 2. РАСЧЕТ И ХАРАКТЕРИСТИКА ПАРАМЕТРОВ СХЕМ ЗАМЕЩЕНИЯ ВОЗДУШНЫХ И КАБЕЛЬНЫХ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧ
2.1. ОБЩАЯ ХАРАКТЕРИСТИКА СХЕМ ЗАМЕЩЕНИЯ
Параметры фаз линий электропередач равномерно распределены по ее длине, т.е. линия электропередачи представляет собой цепь с равномерно распределенными параметрами. Точный расчет схемы, содержащей такую цепь, приводит к сложным вычислениям. В связи с этим при расчете линий электропередач в общем случае применяют упрощенные Т- и П-образные схемы замещения с сосредоточенными параметрами (рис. 2.1). Погрешности электрического расчета линии при Т- и П-образной схемах замещения примерно одинаковы. Они зависят от длины линии.
Допущение о сосредоточенности реально равномерно распределенных параметров по длине ЛЭП справедливо при протяженности воздушных линий (ВЛ), не превышающей 300—350 км, а для кабельных линий (КЛ) 50—60 км. Для ЛЭП большей длины применяют различные способы учета распределенности их параметров1.
Моделирование протяженных ЛЭП рассматривается в параграфе 2.5.
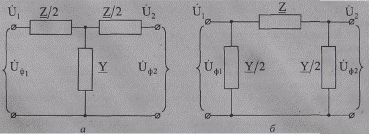
Рис. 2.1. Схема замещения ЛЭП с сосредоточенными параметрами: а — Т-образная; 6 — П-образная
Размерность схемы ЭС и, соответственно, системы моделирующих уравнений определяется числом узлов схемы. Поэтому в практических расчетах, в особенности с использованием ЭВМ, чаще используют П-образную схему замещения, имеющую одно преимущество — меньшую в 1,5 раза размерность схемы в сопоставлении с моделированием ЛЭП Т-образной схемой. Поэтому дальнейшее изложение будет вестись применительно к П-образной схеме замещения ЛЭП [24, 25].
Выделим в схемах замещения продольные элементы — сопротивления ЛЭП Z=R+jX и поперечные элементы — проводимости Y=G+jB (рис.1.1). Значения указанных параметров для ЛЭП определяются по общему выражению
П = По·L, (2.1)
где П {R0,X0,g0,b0}— значение продольного или поперечного параметра, отнесенного к 1 км линии протяженностью L, км: Иногда эти параметры именуются погонными.
Для ЛЭП конкретного исполнения и класса напряжения используют частные случаи этих схем в зависимости от физического проявления и величины (значения) соответствующего параметра. Рассмотрим кратко суть этих параметров.
Активное сопротивление обуславливает нагрев проводов (тепловые потери) и зависит от материала токоведущих проводников и их сечения. Для линий с проводами небольшого сечения, выполненных цветным металлом (алюминий, медь), активное сопротивление принимают равным омическому (сопротивлению постоянному току), поскольку проявление поверхностного эффекта при промышленных частотах 50—60 Гц незаметно (около 1 %). Для проводов большого сечения (500 мм2 и более) явление поверхностного эффекта при промышленных частотах значительно.
Активное погонное сопротивление линии определяется по формуле, Ом/км,
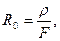 (2.2)
(2.2)
где ρ — удельное активное сопротивление материала провода, Ом-мм2/км; F— сечение фазного провода (жилы), мм2. Для технического алюминия в зависимости от его марки можно принять ρ = 29,5—31,5 Ом · мм 2/км, для меди ρ = 18,0— 19,0Ом·мм2/км.
Активное сопротивление не остается постоянным. Оно зависит от температуры провода, которая определяется температурой окружающего воздуха (среды), скоростью ветра и значением проходящего по проводу тока.
Омическое сопротивление упрощенно можно трактовать как препятствие направленному движению зарядов узлов кристаллической решетки материала проводника, совершающих колебательные движения около равновесного состояния. Интенсивность колебаний и, соответственно, омическое сопротивление возрастают с ростом температуры проводника.
Зависимость активного сопротивления от температуры провода t определяется в виде
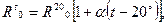 (2-3)
(2-3)
где 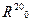 — нормативное значение сопротивления Ro, рассчитывается по формуле (2.2), при температуре проводника t = 200C; α— температурный коэффициент электрического сопротивления, Ом/град (для медных, алюминиевых и сталеалюминевых проводов α = 0,00403, для стальных α = 0,00455).
— нормативное значение сопротивления Ro, рассчитывается по формуле (2.2), при температуре проводника t = 200C; α— температурный коэффициент электрического сопротивления, Ом/град (для медных, алюминиевых и сталеалюминевых проводов α = 0,00403, для стальных α = 0,00455).
Трудность уточнения активного сопротивления линий по (2.3) заключается в том, что температура провода, зависящая от токовой нагрузки и интенсивности охлаждения, может заметно превышать температуру окружающей среды. Необходимость такого уточнения может возникнуть при расчете сезонных электрических режимов [26].
При расщеплении фазы ВЛ на n одинаковых проводов в выражении (2.2) необходимо учитывать суммарное сечение проводов фазы:
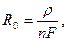 (2.4)
(2.4)
Индуктивное сопротивление обусловлено магнитным полем, возникающим вокруг и внутри проводника при протекании по нему переменного тока. В проводнике наводится ЭДС самоиндукции, направленная в соответствии с принципом Ленца, противоположно ЭДС источника
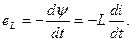
Противодействие, которое оказывает ЭДС самоиндукции изменению ЭДС источника, и обуславливает индуктивное сопротивление проводника. Чем больше изменение потокосцепления dΨ/dt, определяемое частотой тока ω=2πf (скоростью изменения тока di / dt), и величина индуктивности фазы L, зависящая от конструкции (разветвленное™) фазы и трехфазной ЛЭП в целом, тем больше индуктивное сопротивление элемента X =ωL. To есть для одной и той же линии (или просто электрической катушки) с ростом частоты питающего тока f индуктивное сопротивление увеличивается. Естественно, что при нулевой частоте (ω=2πf=0), например, в сетях постоянного тока, индуктивное сопротивление ЛЭП отсутствует.
На индуктивное сопротивление фаз многофазных ЛЭП оказывает влияние также взаимное расположение фазных проводов (жил). Кроме ЭДС самоиндукции, в каждой фазе наводится противодействующая ей ЭДС взаимоиндукции. Поэтому при симметричном расположении фаз, например, по вершинам равностороннего треугольника, результирующая противодействующая ЭДС во всех фазах одинакова, а следовательно, одинаковы пропорциональные ей индуктивные сопротивления фаз. При горизонтальном расположении фазных проводов потокосцепление фаз неодинаково, поэтому индуктивные сопротивления фазных проводов отличаются друг от друга. Для достижения симметрии (одинаковости) параметров фаз на специальных опорах выполняют транспозицию (перестановку) фазных проводов.
Индуктивное сопротивление, отнесенное к 1 км линии, определяется по эмпирической формуле, Ом/км,
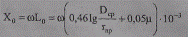 (2.5)
(2.5)
Если принять частоту тока 50 Гц, то при указанной частоте ω=2πf= 314рад/с для проводов из цветных металлов (μ = 1) получим, Ом/км,
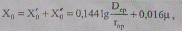 (2.6)
(2.6)
а при частоте 60 Гц соответственно (ω = 376,8 рад/с), Ом/км
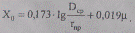 (2.7)
(2.7)
При сближении фазных проводов влияние ЭДС взаимоиндукции возрастает,
что приводит к уменьшению индуктивного сопротивления ЛЭП (табл. П 1.10 – П 1.11). Особенно заметно снижение индуктивного сопротивления (в 3—5 раз) в кабельных линиях. Разработаны компактные ВЛ высокого и сверхвысокого напряжения повышенной пропускной способности со сближенными фазами с использованием эффекта взаимного влияния цепей и сниженным на 25—30 % индуктивным сопротивлением [2, 3, 7].
Величина среднегеометрического расстояния между фазными проводами (жилами), м,
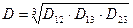 (2.8)
(2.8)
зависит от расположения фазных проводов (шин). Фазы ВЛ могут располагаться горизонтально или по вершинам треугольника, фазные шины токопроводов в горизонтальной или вертикальной плоскости, жилы трехжильного кабеля — по вершинам равностороннего треугольника. Значения Dcp и rnp должны иметь одинаковую размерность.
При отсутствии справочных данных фактический радиус многопроволочных проводов rпр можно определить по суммарной площади сечения токоведущей и стальной части провода, увеличив его с учетом скручивания на 15—20 %, т.е.
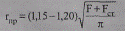 (2.9)
(2.9)
Отметим, что индуктивное сопротивление состоит из двух составляющих: внешней и внутренней. Внешнее индуктивное сопротивление X’0 определяется внешним магнитным потоком, образованным вокруг проводов, и значениями Dcp и rпр. Естественно, что с уменьшением расстояния между фазами растет влияние ЭДС взаимоиндукции и индуктивное сопротивление снижается, и наоборот. У кабельных линий с их малыми расстояниями между токоведущими жилами (на два порядка меньше, чем в ВЛ) индуктивное сопротивление значительно (в 3—5 раз) меньше, чем у воздушных. Для определения Хо кабельных линий формулы (2.5) и (2.6) не применяют, так как они не учитывают конструктивных особенностей кабелей.
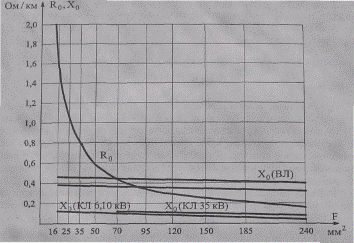
Рис. 2.2. Изменение Ro и Хо в зависимости от сечений проводов и жил кабелей из цветных металлов
Поэтому при расчетах пользуются заводскими данными об индуктивном сопротивлении кабелей [25, 27], приведенными в прил. 1 (табл. П 1.3 и П 1.4). Внутреннее индуктивное сопротивление Х’’0 определяется внутренним потоком, замыкающимся в проводах.
Для стальных проводов (см. параграф 2.4) его значение находится в зависимости от токовой нагрузки и дается в справочной литературе и табл. П 1.7 и П 1.8.
Таким образом, активное сопротивление ЛЭП зависит от материала, сечения и температуры провода. Зависимость Ro = φ(F) обратно пропорциональна сечению провода, ярко выражена при малых сечениях, когда Ro имеет большие значения, и мало заметна при больших сечениях проводов. Индуктивное сопротивление ЛЭП определяется исполнением линии, конструкцией фазы (рис. 2.2) и практически не зависит от сечения проводов (значение lg(Dcp /гпр) ≈ const).
Емкостная проводимость обусловлена емкостями между фазами, фазными проводами (жилами) и землей. В схеме замещения ЛЭП используется расчетная (рабочая) емкость плеча эквивалентной звезды, полученной из преобразования треугольника проводимостей С = Cа0 + ЗСаЬ в звезду (рис. 2.3, в).
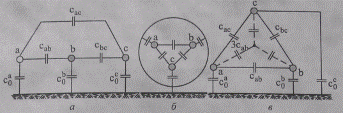
Рис. 2.3. Емкости трехфазных линий электропередачи:
а—воздушной линии; б — кабельной линии; в — преобразование треугольника емкостей в звезду
В практических расчетах рабочую емкость трехфазной ВЛ с одним проводом в фазе на единицу длины (Ф/км) определяют по формуле
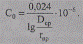 (2.10)
(2.10)
Рабочая емкость кабельных линий существенно выше емкости ВЛ, так как жилы кабеля очень близки друг к другу и заземленным металлическим оболочкам. Кроме того, диэлектрическая проницаемость кабельной изоляции значительно больше единицы — диэлектрической проницаемости воздуха. Большое разнообразие конструкций кабеля, отсутствие их геометрических размеров усложняет определение ее рабочей емкости, в связи с чем на практике пользуются данными эксплуатационных или заводских замеров (например, табл. 2.1).
Емкостная проводимость ВЛ и КЛ, См/км, определяется по общей формуле
b0=ωc0 (2.10 а)
Таблица 2.1
Рабочая емкость Со(·10-6), Ф/км, трехжильных кабелей с поясной изоляцией
| Напряжение, | Сечение жилы мм2 | ||||||||||
| кВ | |||||||||||
| До1 | 0,35 0,20 - | 0,40 0,23 - | 0,50 0,28 0,23 | 0,53 0,31 0,27 | 0,630 0,36 0,29 | 0,72 0,40 0,31 | 0,77 0,42 0,32 | 0,81 0,46 0,37 | 0,86 0,51 0,44 | 0,86 0,53 0,45 | 0,58 0,60 |
С учетом (2.10 а) для воздушной линии при частоте тока 50 Гц имеем, См/км,
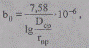 (2.11)
(2.11)
а для ВЛ с частотой питающего напряжения 60 Гц получим, См/км,
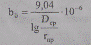 (2.12)
(2.12)
Емкостная проводимость КЛ зависит от конструкции кабеля и указывается заводом-изготовителем, но для ориентировочных расчетов она может быть оценена по формуле (2.11).
Под действием приложенного к линии напряжения через емкости линий протекают емкостные (зарядные) токи. Тогда расчетное значение емкостного тока на единицу длины, кА/км,
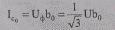 (2.13)
(2.13)
и отвечающая ему зарядная мощность трехфазной ЛЭП, Мвар/км,
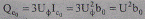 (2.14)
(2.14)
зависят от напряжения в каждой точке линии.
Значение зарядной мощности для всей ЛЭП определяется через действительные (расчетные) напряжения начала и конца линии, Мвар,
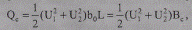 (2.15)
(2.15)
либо приближенно по номинальному напряжению линии
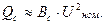 (2.16)
(2.16)
Для кабелей 6—35 кВ с бумажной изоляцией и вязкой пропиткой известны генерации реактивной мощности q0 на один километр линии (табл. П 1.4), с учетом которой общая генерация КЛ определится в виде
QCкл=q0L. (2.17)
ЛЭП с поперечной емкостной проводимостью, потребляющая из сети опережающий напряжение емкостный ток, следует рассматривать как источник реактивной (индуктивной) мощности, чаще называемой зарядной. Имея емкостной характер, зарядная мощность уменьшает индуктивную составляющую нагрузки, передаваемой по линии к потребителю.
В схемах замещения ВЛ, начиная с номинального напряжения 110 кВ, и в КЛ 35 кВ и более (рис. 2.6) следует учитывать поперечные ветви (шунты) в виде емкостных проводимостей Вс или генерируемых ими реактивных мощностей Qc.
Расстояние между фазами ЛЭП в каждом классе напряжения, особенно для ВЛ, практически одинаково, что и определяет неизменность результирующего потокосцепления фаз и емкостного эффекта линий. Поэтому для ВЛ традиционного исполнения (без глубокого расщепления фаз и специальных конструкций опор) реактивные параметры мало зависят от конструктивных характеристик линии, так как отношение расстояния между фазами и сечения (радиуса) проводов практически неизменны, что в приведенных формулах отражено логарифмической функцией.
При выполнении фаз ВЛ 35—220 кВ одиночными проводами их индуктивное сопротивление изменяется в узких пределах: Хо =(0,40-0,44) Ом/км, а емкостная
проводимость лежит в пределах bо = (2,6 - 2,8) • 10-6 См/км. Влияние изменения площади сечения (радиуса) жил кабеля на Хо более заметно, чем в ВЛ. Поэтому для КЛ имеем более широкое изменение индуктивного сопротивления: Хо ≈ (0,06-0,15) Ом/км. Для кабельных линий всех марок и сечений напряжением 0,38—10 кВ индуктивное сопротивление лежит в более узком интервале (0,06—0,10 Ом/км) и определяется из таблиц физико-технических данных кабелей.
Среднее значение зарядной мощности на 100 км для ВЛ 110кВ составляет около 3,5 Мвар, для ВЛ 220 кВ — 13,5 Мвар, для ВЛ 500 кВ — 95 Мвар. Учет этих показателей позволяет исключить значительные ошибки при расчете параметров линий или использовать указанные параметры в приближенных расчетах, например для оценки по реактивным параметрам ВЛ ее протяженности (км) в виде
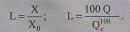 (2.18)
(2.18)
Активная проводимость обусловлена потерями активной мощности ΔР из-за несовершенства изоляции (утечки по поверхности изоляторов, токов проводимости (смещения) в материале изолятора) и ионизации воздуха вокруг проводника вследствие коронного разряда. Удельная активная проводимость определяется по общей формуле для шунта, См/км,
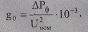 (2.19)
(2.19)
где UH0M — номинальное напряжение ЛЭП в кВ.
Потери в изоляции ВЛ незначительны, и явление коронирования в ВЛ возникает только при превышении напряженности электрического поля у поверхности провода, кВмакс/см:
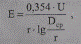 (2.19 а)
(2.19 а)
критическая величина около 17—19 кВ/см. Такие условия для коронирования возникают в ВЛ 110 кВ и более высокого напряжения.
Коронирование и, соответственно, потери активной мощности сильно зависят от напряжения ВЛ, радиуса провода, атмосферных условий и состояния поверхности провода. Чем больше рабочее напряжение и меньше радиус проводов, тем больше напряженность электрического поля. Ухудшение атмосферных условий (высокая влажность воздуха, мокрый снег, изморозь на поверхности проводов), заусенцы, царапины также способствуют росту напряженности электрического поля и, соответственно, потерь активной мощности на коронирование. Коронный разряд вызывает помехи на радио- и телевизионный прием, коррозию поверхности проводов ВЛ.
Для снижения потерь на корону до экономически приемлемого уровня правилами устройства электроустановок (ПУЭ) [12] установлены минимальные сечения (диаметры) проводов. Например, для ВЛ 110 кВ — АС 70 (11,8 мм), для ВЛ 220 кВ — АС 240 (21,6 мм).
Потери мощности на коронирование учитывают при моделировании ВЛ с номинальным напряжением 330 кВ и более (рис. 2.5)2.
2 В технико-экономических расчетах, связанных с учетом стоимости потерь электроэнергии, потери на коронирование следует учитывать в ВЛ начиная с напряжения 220 кВ, диэлектрические потери в КЛ — с напряжения 35 кВ.
В КЛ под влиянием наибольшей напряженности находятся слои поясной изоляции у поверхности жил кабеля. Чем выше рабочее напряжение кабеля, тем заметнее токи утечки через материал изоляции и нарушение ее диэлектрических свойств. Последние характеризуются тангенсом угла диэлектрических потерь tg5, принимаемым по данным завода-изготовителя.
Активная проводимость кабеля на единицу длины
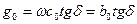 (2.20)
(2.20)
и соответствующий ток утечки в изоляции кабеля, А,
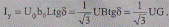 (2.21)
(2.21)
Тогда диэлектрические потери в материале изоляции КЛ, МВт,
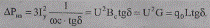 (2.22)
(2.22)
Их следует учитывать для КЛ с номинальным напряжением 110 кВ и выше.
2.2. ВОЗДУШНЫЕ ЛЭП С РАСЩЕПЛЕННЫМИ ФАЗАМИ
Если каждая фаза выполнена двумя и более проводами, то такая конструкция фазы считается расщепленной. В линиях традиционного исполнения с номинальным напряжением 330 кВ фазы расщеплены на два провода, в линиях 500 кВ — на три провода, в линиях 750 кВ — на четыре-пять проводов. В Красноярской энергосистеме эксплуатируется ВЛ 220 кВ Дивногорск — Красноярск с расщеплением фазы на два провода. Существуют экспериментальные ВЛ [2, 7] повышенной пропускной способности с 6—8 и более проводами в фазе.
Основным назначением расщепления фаз является увеличение пропускной способности и снижение (ограничение) коронирования ВЛ до экономически приемлемого уровня. Увеличение пропускной способности достигается при неизменном номинальном напряжении и сечении путем снижения индуктивного сопротивления ЛЭП. Так, при выполнении фазы n одинаковыми проводами погонное активное сопротивление фазы уменьшается в n раз, т. е.
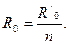
Однако для ВЛ указанных номинальных напряжений характерны соотношения между параметрами Ro«Xo. Поэтому увеличение пропускной способности достигается в основном снижением индуктивного сопротивления. При n проводах в фазе увеличивается эквивалентный радиус расщепления конструкции фазы (рис. 2.4):
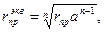 (2-23)
(2-23)
где а — расстояние между проводами в фазе, равное 40—60 см.
Анализ зависимости (2.23) показывает, что эквивалентный радиус фазы изменяется в диапазоне от 9,3 см (при n = 2) до 65 см (при n = 10) и мало зависит от сечения провода. Основным фактором, определяющим изменение 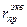 ,является количество проводов в фазе [2, 7, 8]. Так как эквивалентный радиус расщепленной фазы намного больше действительного радиуса провода нерасщепленной фазы (
,является количество проводов в фазе [2, 7, 8]. Так как эквивалентный радиус расщепленной фазы намного больше действительного радиуса провода нерасщепленной фазы ( 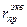 »rпр), то индуктивное сопротивление такой ВЛ, определяемое по преобразованной формуле вида (1.6), Ом/км, уменьшается:
»rпр), то индуктивное сопротивление такой ВЛ, определяемое по преобразованной формуле вида (1.6), Ом/км, уменьшается:
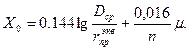 (2.24)
(2.24)
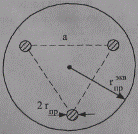
Рис. 2.4. К определению радиуса конструкции расщепленной фазы
Снижение Хо достигаемое, в основном, за счет уменьшения внешнего сопротивления Х'о,относительно невелико. Например, при расщеплении фазы воздушной линии 500 кВ на три провода — до 0,29—0,30 Ом/км, т. е. примерно на треть. Соответственно с уменьшением сопротивления Z =(Ro + jX0)L = ZejΨ увеличивается пропускная способность (идеальный предел) линии:
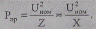 (2.25)
(2.25)
Естественно, что с увеличением эквивалентного радиуса фазы 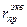 снижается напряженность электрического поля вокруг фазы и, следовательно, потери мощности на коронирование. Тем не менее, суммарные значения этих потерь для ВЛ высокого и сверхвысокого напряжения (220 кВ и более) составляют заметные величины, учет которых необходим при анализе режимов линий указанных классов напряжений (рис. 2.5).
снижается напряженность электрического поля вокруг фазы и, следовательно, потери мощности на коронирование. Тем не менее, суммарные значения этих потерь для ВЛ высокого и сверхвысокого напряжения (220 кВ и более) составляют заметные величины, учет которых необходим при анализе режимов линий указанных классов напряжений (рис. 2.5).
Расщепление фазы на несколько проводов увеличивает емкость ВЛ и соответственно емкостную проводимость:
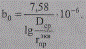 (2.26)
(2.26)
Например, при расщеплении фазы ВЛ 220 кВ на два провода проводимость
возрастает с 2,7·10-6 до 3,5·10-6 См/км. Тогда зарядная мощность ВЛ 220 кВ средней протяженности, например 200 км, составляет
Qc = b0LU2н; = 3,5 10-6 · 200 ·2202= 33,88 Мвар,
что соизмеримо с передаваемыми мощностями по ВЛ данного класса напряжения, в частности, с натуральной мощностью линии

(2.27)
Характерные данные и соотношения для параметров ЛЭП различного класса напряжения приведены в табл. 2.2.
Таблица 2.2
Конструктивные и схемно-режимные параметры воздушных линий
| Uh,kB | 0,22 — 0,38 | 6—10 | |||||||||
| D,m | 0,4 — 0,5 | 0,7 — 0,9 | 2,5 — 3,0 | 4,0 — 4,5 | 5,5 — 6,0 | 7,0 — 7,5 | 8,5 — 9,0 | 10,0 — 12,0 | |||
| *nиз,шт | 3 — 4 | 6 — 7 | 9—10 | 12—14 | 19 — 22 | 31 — 34 | |||||
| Длина пролета, м | 35 — 45 | 60 — 80 | 150 — 200 | 170 — 250 | 200 — 250 | 250 — 300 | 300 — 400 | 350 — 450 | |||
| Х0, Ом/км | 0,29 — 0,35 | 0,33 — 0,37 | 0,40 — 0,41 | 0,41—0,43 | 0,42 — 0,44 | 0,42 — 0,44 | 0,32 | 0,29 | |||
| bо·10-6 См /км | 2,6 — 2,8 | 3,4 — 3,5 | 3,6 — 3,9 | ||||||||
| Qc·10-2 Мвар/ км | — | — | — | 3 — 4 | 6 — 7 | 12—13 | 40 — 42 | 90 — 95 | |||
| **ΔРо кВт/км | — | — | — | — | — | 1 —2 | 4 — 5 | 8—10 | |||
*nиз- количество изоляторов; ** ΔР0 - потери на коронирование при хорошей погоде
2.3. СХЕМЫ ЗАМЕЩЕНИЯ ЛИНИЙ ЭЛЕКТРОПЕРЕДАЧ
Выше приведена характеристика отдельных элементов схем замещения линий. В соответствии с их физическим проявлением при моделировании электрических сетей используют схемы ВЛ, КЛ и шинопроводов, представленные на рис.2.5 - 2.7. Приведем некоторые обобщающие пояснения к этим схемам.
При расчете симметричных установившихся режимов ЭС схему замещения составляют для одной фазы, т. е. продольные ее параметры, сопротивления Z = R + jX изображают и вычисляют для одного фазного провода (жилы), а при расщеплении фазы — с учетом количества проводов в фазе и эквивалентного радиуса фазной конструкции ВЛ.
Емкостная проводимость Вс, как отмечено в параграфе 2.1, учитывает проводимости (емкости) между фазами, между фазами и землей и отражает генерацию зарядной мощности всей трехфазной конструкции линии:
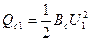 и
и 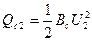
Активная проводимость линии G, изображаемая в виде шунта между фазой (жилой) и точкой нулевого потенциала схемы (землей), включает суммарные потери активной мощности на корону (или в изоляции) трех фаз:
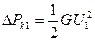 и
и 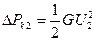 (2.28)
(2.28)
Поперечные проводимости (шунты) Y = G + jB в схемах замещения можно не изображать, а заменять мощностями этих шунтов (рис. 2.5, би рис. 2.6, б). Например, вместо активной проводимости показывают потери активной мощности в ВЛ
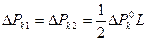 (2.29)
(2.29)
или в изоляции КЛ
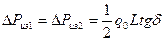 (2.30)
(2.30)
Взамен емкостной проводимости указывают генерацию зарядной мощности
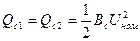 (2.30 а)
(2.30 а)
Указанный учет поперечных ветвей ЛЭП нагрузками упрощает оценку электрических режимов, выполняемых вручную. Такие схемы замещения линий именуют расчетными (рис. 2.5, б и рис. 2.6, б).
В ЛЭП напряжением до 220 кВ при определенных условиях можно не учитывать те или иные параметры, если их влияние на работу сети несущественно. В связи с этим схемы замещения линий, показанные на рис. 2.1, в ряде случаев могут быть упрощены.
В ВЛ напряжением до 220 кВ потери мощности на корону, а в КЛ напряжением до 35 кВ диэлектрические потери незначительны. Поэтому в расчетах электрических режимов ими пренебрегают и соответственно принимают равной нулю активную проводимость (рис. 2.6). Учет активной проводимости необходим для ВЛ напряжением 220 кВ и для КЛ напряжением 110 кВ и выше в расчетах, требующих вычисления потерь электроэнергии, а для ВЛ напряжением 330 кВ и выше также при расчете электрических режимов (рис. 2.5).
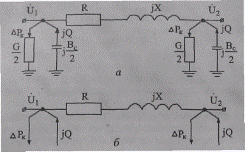
Рис. 2.5. Схема замещения ВЛ 330(220)—500 кВ и КЛ 110—500 кВ:
а — полная с поперечными проводимостями; б — расчетная
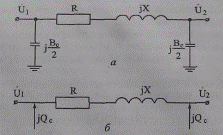
Рис. 2.6. Схема замещения ВЛ 110—220 кВ и КЛ 35 кВ:
а — с емкостными проводимостями, б — с зарядной мощностью вместо проводимостей
Необходимость учета емкости и зарядной мощности линии зависит от соизмеряемости зарядной и нагрузочной мощности. В местных сетях небольшой протяженности при номинальных напряжениях до 35 кВ зарядные токи и мощности значительно меньше нагрузочных. Поэтому в КЛ емкостную проводимость учитывают только при напряжениях 20 и 35 кВ, а в ВЛ ею можно пренебречь.
В районных сетях (110 кВ и выше) со значительными протяженностями (40—50 км и больше) зарядные мощности могут оказаться соизмеримыми с нагрузочными и подлежат обязательному учету либо непосредственно (рис. 2.6, б), либо введением емкостных проводимостей (рис. 2.6, а).
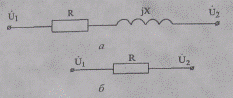
Рис. 2.7. Схема замещения: а — ВЛ 0,38—35 кВ и КЛ 0,38—20 кВ;
б — КЛ 0,38—10 кВ малых сечений
В проводах ВЛ при малых сечениях (16—35 мм2) преобладают активные сопротивления, а при больших сечениях (240 мм2 и более в районных сетях напряжением 220 кВ и выше) свойства сетей определяются их индуктивностями. Активные и индуктивные сопротивления проводов средних сечений (50—185 мм2) близки друг к другу. В КЛ напряжением до 10 кВ небольших сечений (50 мм2 и менее) определяющим является активное сопротивление, и в таком случае индуктивные сопротивления могут не учитываться (рис. 2.7, б).
Необходимость учета индуктивных сопротивлений зависит также от доли реактивной составляющей тока в общей электрической нагрузке. При анализе электрических режимов с низкими коэффициентами мощности (cosφ<0,8) индуктивные сопротивления КЛ необходимо учитывать. В противном случае возможны ошибки, приводящие к уменьшению действительной величины потери напряжения (см. гл. 5).
Схемы замещения ЛЭП постоянного тока могут рассматриваться как частный случай схем замещения ЛЭП переменного тока при X = 0 и b = 0.
2.4. ЛЭП СО СТАЛЬНЫМИ ПРОВОДАМИ
Основное достоинство стальных проводов — их высокие механические свойства. В частности, временное сопротивление на разрыв стальных проводов достигает 600—700 МПа (60—70 кг/мм2) и более. Поэтому стальные провода применяют при выполнении больших переходов через естественные препятствия (широкие реки, горные ущелья
и т. п.).
Однако сталь обладает значительно более высоким электрическим сопротивлением (удельное сопротивление ρ достигает величины 130 Ом·мм2/км) по сравнению с медью и алюминием, которое зависит от сорта стали, способа изготовления провода и от величины тока, протекающего по проводу. Поэтому передача больших мощностей на значительные расстояния затруднена вследствие больших потерь напряжения и электроэнергии.
При передаче по распределительным сетям 6, 10 кВ небольших мощностей (до нескольких сотен кВт), в слабо загруженных сетях до 1000 В монтируют ВЛ со стальными проводами. Кроме того, провода из стали (тросы) используют как элементы повторного заземления низковольтных сетей и устройств грозозащиты высоковольтных ВЛ.
Стальные провода изготавливают из оцинкованных проволок. Без оцинковки срок службы стальных проводов мал, провода ржавеют и становятся непригодными для работы на воздушных линиях электропередачи [11].
Сталь — это ферромагнитный материал, и поэтому стальные провода обладают большой внутренней индуктивностью. Активные сопротивления стальных проводов, так же как и реактивные, зависят от величины протекающего в них тока. При токах, близких к нулю, когда магнитный поток в проводе очень мал, активное и омическое сопротивления проводов практически одинаковы. Разница между этими сопротивлениями тем больше, чем больше магнитная проницаемость стали и диаметр провода. Стальные провода на линиях переменного тока подвергаются постоянному перемагничиванию, что связано с затратами энергии, возрастающими с увеличением тока. Кроме того, растут потери на вихревые токи и резко проявляется поверхностный эффект. Названные потери активной мощности учитывают соответствующими составляющими активного сопротивления стальных проводов:
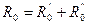
где R'o— сопротивление постоянному току (омическое),
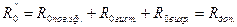
Сталь обладает большей магнитной проницаемостью (μ> 1), чем цветные металлы (медь и алюминий). Активное сопротивление переменному току ЛЭП со стальными проводами выше активного сопротивления ЛЭП того же сечения из меди или алюминия. Величина дополнительных потерь зависит от магнитного потока Ф в сечении провода, а магнитный поток определяется магнитной проницаемостью материала провода р. и напряженностью магнитного поля Н:
Ф = BF = μHF,
где В — магнитная индукция, a F — площадь поперечного сечения провода.
Напряженность магнитного поля пропорциональна току в проводе (H~I), a магнитная индукция определяется как током, так и степенью насыщения стали. Поэтому при малых значениях тока магнитный поток, а значит, и дополнительное сопротивление провода растут пропорционально его значению. При некоторой величине тока магнитная индукция становится практически постоянной величиной (насыщение стали) и сопротивление стабилизируется. При дальнейшем увеличении протекающего тока сопротивление начинает уменьшаться вследствие уменьшения магнитной проницаемости стали. Кривые изменения активного сопротивления стальных однопроволочных и многопроволочных проводов от тока нагрузки представлены на рис. 2.8 (кривая 1).
Активное сопротивление стальных проводов зависит от многих факторов (химического состава стали, токовой нагрузки и др.), является очень сложной функцией и его трудно выразить математической формулой. Для определения активных сопротивлений стальных проводов используют табличные данные (прил. 1, табл. П 1.7, П 1.8), составленные на основании измерений для разных марок и сечений проводов в зависимости от величины тока.
Индуктивное сопротивление стального провода также определяется двумя составляющими: внешним индуктивным сопротивлением 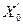 и внутренним индуктивным сопротивлением
и внутренним индуктивным сопротивлением 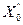 , Ом/км:
, Ом/км:
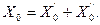
Внешнее индуктивное сопротивление, Ом/км, обусловлено внешним магнитным потоком, зависит от геометрических размеров линии и рассчитывается по формуле
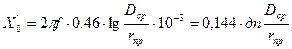
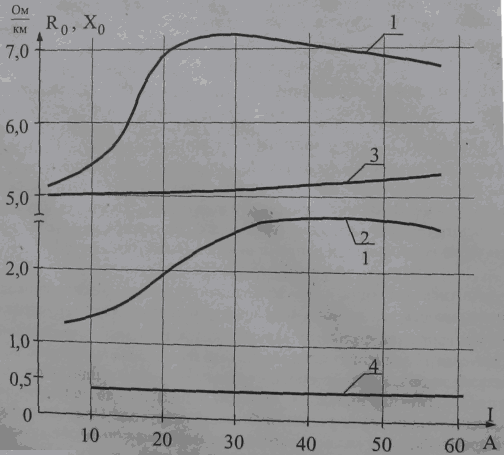
Рис.2.8. Активные (1) и индуктивные (2) сопротивления стальных проводов;
сопротивление постоянному току (3) и индуктивное сопротивление алюминиевых проводов (4)
Внутреннее индуктивное сопротивление обусловлено магнитным потоком, замыкающимся внутри провода, и определяется магнитной проницаемостью, которая, в свою очередь, зависит не только от конструкции и химического состава стали провода, но и от тока, протекающего в проводе:
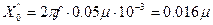
Для определения внутреннего индуктивного сопротивления пользуются экспериментальными данными (прил. 1, табл. П 1.7—П 1.8), внешнее индуктивное сопротивление определяется по формуле (2.31).
Внутреннее индуктивное сопротивление стальных проводов по своей величине значительно превышает внешнее индуктивное сопротивление и значительно больше, чем у проводов из цветных металлов. У линии передачи с проводами из цветного металла индуктивное сопротивление в основном обусловлено внешним магнитным потоком. Например, у трехфазной линии с проводами А 50 при среднегеометрическом расстоянии между ними Dcp=l,5 мдоля внутреннего индуктивного сопротивления Х'ов полном Хо составляет всего 4,1 %. Для ВЛ со стальными проводами ПМС 50 при токе 25 А она составляет 58 %, т. е. в 14 раз больше.
На рис. 1.8 показаны для провода ПС 25 кривые изменения активного (кривая 1) и реактивного (кривая 2) сопротивлений в зависимости от величины переменного тока. Для сравнения слабовыраженная кривая 3 показывает изменение сопротивления провода постоянному току, а прямая 4 — индуктивного сопротивления для алюминиевых проводов.
Активные и реактивные сопротивления однопроволочного провода быстро растут с увеличением его диаметра. Поэтому в электрических сетях однопроволочные провода применяют с диаметром не более 5 мм. Провода с сечением 25 мм и выше выполняют многопроволочными.
Многопроволочные провода имеют значительно лучшие электрические характеристики, чем однопроволочные, и почти не зависящие от сечения провода. В многопроволочных проводах, благодаря воздушным промежуткам между отдельными проволоками, из которых свит провод, сопротивление магнитному потоку резко возрастает. Магнитный поток внутри провода уменьшается — уменьшаются активное и реактивное сопротивления провода [11]. В целом удельные активное и реактивное сопротивления стальных проводов в несколько раз превышают аналогичные величины проводов из цветного металла. Это означает, что в таких ЛЭП с увеличением тока нагрузки увеличивается сопротивление стального провода, значительно выше потери напряжения и, соответственно, снижается пропускная способность электропередачи. Вследствие этих причин применение стальных проводов ограничено.
2.5. МОДЕЛИРОВАНИЕ ПРОТЯЖЕННЫХ ЛИНИЙ
Рассмотренное выше моделирование линий электропередачи схемой замещенияс сосредоточенными параметрами, допустимое для воздушных линий длиной до 300—350 км и кабельных линий — 50—60 км, вносит в расчетные параметры более протяженных (длинных) линий ощутимые погрешности, возрастающие с ростом длины ЛЭП.
Однородная ЛЭП представляет собой электрическую цепь с равномерно распределенными параметрами: с сопротивлением Z0=R0+jX0 и проводимостью Yo=g0+jb0, неизменными по длине цепи (рис. 2.9, а). Такое представление линий справедливо при условии полной электростатической и электромагнитной симметрии фаз, что в реальных условиях обеспечивается их транспозицией [10, 11]. Ток и напряжение в линии непре
Дата добавления: 2021-02-19; просмотров: 1757;











