Решение задачи. Определить погонные параметры кабельной линии длиной 5,0 км с номинальным напряжением 10 кВ

ЗАДАЧА 2.1. Требуется определить погонные параметры кабельной линии длиной 5,0 км с номинальным напряжением 10 кВ, прокладываемой в земле и выполненной ка­белем марки СБ 10—3x25, и вычислить параметры схемы замещения этой линии.

Решение

Погонные параметры кабеля СБ 10—3x25 с медными жилами сечением 25 мм² и номинальным напряжением 10 кВ находим по табл. П 1.4.

R_o =0,740 Ом/км, Х_о =0,099 Ом/км, q₀ =8,6 квар/км.

Принимая среднее значение удельного сопротивления для электротехнической меди 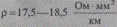рассчитываем погонное активное сопротивление кабеля по

формуле (2.2):

Используя табличные данные для всей линии, имеем:

R = 0,740-5,0 = 3,70 Ом;

Х = 0,099-5,0 = 0,50 Ом;

Q = 8,6-5,0 = 43,0 квар.

Для оценки целесообразности учета емкостной проводимости в схеме замещения

сопоставим зарядную мощность, определяемую этой проводимостью, с длительно допустимой нагрузкой.

Длительно допустимый ток по нагреву для рассматриваемого кабеля равен 120 А [27, табл. 2—5].

Этому току соответствует полная мощность:

Следовательно,

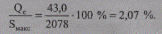
Полученная величина зарядной мощности не может оказать заметного влияния на результаты расчетов электрических режимов распределительной сети 10 кВ, хотя и со­измерима с мощностью небольших потребителей этих сетей. Поэтому можно эту мощ­ность не учитывать и исключить из схемы замещения емкостную проводимость.

Для индуктивного сопротивления имеем:

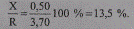
Индуктивное сопротивление представляет заметную величину, поэтому должно быть учтено в схеме замещения (рис. 2.11), содержащей продольные ак­тивное и индуктивное сопротивления.

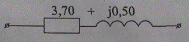
Рис. 2.11. Схема замещения кабельной линии 10 кВ

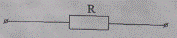
Рис. 2.12. Схема замещения кабельной линии с жилами относительно небольшого сечения

Влияние индуктивного сопротивления на потери напряжения может быть существенным в КЛ, питающей потребителей с низким коэффициентом мощно­сти (см. задачу 5.4).

При меньших сечениях кабелей, особенно с алюминиевыми жилами, вели­чина индуктивного сопротивления не превышает 10%, поэтому может не учиты­ваться. В таких условиях кабельная линия представляется схемой замещения, со­держащей только активное сопротивление (рис. 2.12).

ЗАДАЧА 2.2

В связи с реконструкцией распределительной сети на участке длиной 10,0 км планируется замена воздушной линии с номинальным напряжением 6 кВ, вы­полненной проводом А 50, на ВЛ 10 кВ с проводом АС 50/8. Демонтируемая ВЛ 6 кВ сооружена на одностоечных цельных деревянных опорах с расположением проводов по вершинам равнобедренного треугольника (рис. 2.13, а), новая ВЛ 10 кВ спроектирована на одностоечных деревянных опорах с железобетонными приставками и металлическими траверсами, с расположением проводов по вер­шинам равностороннего треугольника (рис. 2.13, б).

Требуется сопоставить погонные параметры ВЛ 6 кВ и 10 кВ и их допусти­мые мощности.

Решение

Определим параметры схемы замещения линий, руководствуясь физиче­скими характеристиками проводов и данными конструкции ВЛ. Расчетные па­раметры сопоставим с табличными.

Примем среднее значение удельного активного сопротивления для алюми­ниевой проволоки ρ=30 Ом*мм²/км из диапазона 29,0—31,5 с. Тогда погонное активное сопротивление приближенно можно определить по формуле

Это значение равнопригодно для проводов А 50 и АС 50/8, так как сопро­тивление стального троса (ρ=130 Ом*мм²/км) значительно больше алюминие­вой части провода, несущей подавляющую токовую нагрузку. Для меньших сече­ний, например А 25 и АС 25, различие R_o более ощутимо.

Уточним значение R_o по известной марке электротехнической проволоки (табл. П 1.9). Например, для проволоки марки АПТ (полутвердая) имеем ρ=29,3

Ом*мм²/км.

Рис 2.13. Промежуточные одностоечные опоры ВЛ на напряжение 6—10 кВ (размеры в метрах)

Отметим, что фактическая площадь сечения многопроволочных проводов составляет около 98—99 % от номинальной [11, 19, 25, 27, 29]. В данном случае для проводов А 50 и АС 50/8 имеем F_факт=48,2мм². Тогда с учетом увеличения фактической длины многопроволочных проводов на 2—3 % из-за скрутки и уд­линения на 0,1—0,2 % вследствие провеса имеем

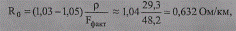
что незначительно отличается от расчетного значения, полученного по усреднен­ным и номинальным данным.

Из сопоставления расчетного значения R_o= 0,600 Ом/км с табличными значениями различных источников [9, 11, 19, 25, 27, 29], лежащих в пределах Ro=0,592 - 0,65, видно, что изменение расчетного значения Ro находится в пределах погрешности исходных данных о ВЛ, а его величина может быть принята в каче­стве фактического значения погонного активного сопротивления.

Определим реактивные параметры ВЛ.

Среднегеометрическое расстояние между фазами для ВЛ 6 кВ (рис. 2.13, а)

для ВЛ 10кВ(рис. 2.13, б)

Не используя справочных данных, фактический радиус многопроволочных проводов можно определить непосредственно по суммарной площади алюминие­вой и стальной части проводов, увеличив ее (из-за скрутки многопроволочных проводов) на 10—15 %, для АС 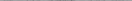50/8 получим

что соответствует фактическим данным провода

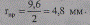
Для провода А 50 имеем

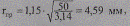
а фактические данные г_пр =4,5 мм (табл. П 1.9).

С учетом найденных расчетных значений D_cp и г_пр, определим погонные индуктивные сопротивления:

для ВЛ 6 кВ

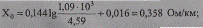
для ВЛ 10 кВ

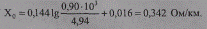
С достаточной точностью для обеих ВЛ можно принять Х_о= 0,35 Ом/км.

Из сопоставления этого результата с табличными значениями для наиболее часто используемых сечений алюминиевых и сталеалюминевых проводов сечени­ем 35, 50,70 мм² для различных конструкций ВЛ 6 и 10 кВ (D_cp = 1 м) [11, 24, 25, 27, 29], видно, что реактивное сопротивление линии Хо можно рассматривать как константу, характерное значение которой можно принять около 0,35—0,36 Ом/км, не выполняя расчетов, требующих часто оперативно недоступных данных о конструкции конкретной ВЛ, а главное, не дающих для практики значимых уточнений результатов.

Дадим оценку емкостной проводимости линий.

Для ВЛ 6 кВ имеем

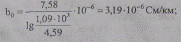
для ВЛ 10 кВ

Примем среднее значение b_о≈3,27*10^-6 См/км . Найденная емкостная про­водимость в 86/3,35=25,7 раза меньше емкостной проводимости кабельной ли­нии того же номинального напряжения (задача 2.1).

Зарядная мощность ВЛ будет также в 25,7 раза меньше зарядной мощности кабельной линии того же класса напряжения, влияние которой на режим этой ли­нии оценивается как несущественное. Следовательно, в схеме замещения воздуш­ных линий этим влиянием с еще большим основанием можно пренебречь. Этот вывод с достаточным основанием может быть распространен на ВЛ до 35 кВ включительно.

Индуктивное сопротивление как в данном случае

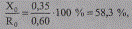
так и для всего диапазона сечений проводов (25—95 мм²), применяемых для ВЛ 6,10 кВ, соизмеримо с активным сопротивлением

поэтому оно должно быть учтено в схеме замещения, которая представляется в рассматриваемых условиях (рис. 2.14) продольными активным и индуктивным сопротивлениями:

Z = (0,60 + j0.35)*10,0 = 6,00 + j3,50 Ом.

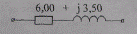
Рис. 2.14. Схема замещения ВЛ 6—10 кВ

Рассматриваемые ВЛ 6 кВ и 10 кВ характеризуются практически одинако­выми параметрами схемы замещения и предельным током по условиям нагрева, равным 210—215 А, определяемый по табл. П 1.9. Этому току соответствует пол­ная мощность для ВЛ 6 кВ S_max=√3*6,0* 210*10^-3 =2,18 МВА, а для ВЛ 10 кВ S_max= √3*10,0* 210*10^-3 =3,64 МВА.

Таким образом, в данном случае перевод ВЛ с 6 кВ на 10 кВ при неизмен­ном сечении проводов увеличивает на две трети предельную мощность электро­передачи.

ЗАДАЧА 2.3

Определить потребность в проводе АС 50/8 для монтажа (реконструкции) ВЛ 10 кВ протяженностью 5,0 км.

Решение

Потребность проводникового материала определяется в виде общего веса и суммарной протяженности проводов трех фаз на основе оценки (приближенного рас­чета) по расчетным (каталожным) данным или по расчетам физико-геометрических характеристик провода.

1. Найдем расчетный вес сталеалюминевого провода АС 50/8 по табл. П 1.9, он составляет G_o = 196 кг/км. Тогда общий вес проводов трех фаз

С учетом провеса, затрат провода на монтажные концы и вязки, расход провода увеличивается на 2—3%. В итоге суммарная протяженность провода

с общим весом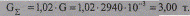

2. Определим вес провода на основе физико-геометрических характеристик. Объем алюминиевой части проводов фаз

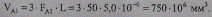
Плотность (объемный вес) алюминия по табл. П 1.1 составляет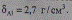

Определим вес фаз:

Объем стального троса

Вес стального троса (δ_ст =7,9 г/cm³ ) составит

Общий вес проводов фаз

Действительная длина проводов фаз возрастает из-за их провеса f (рис. 2.15), с учетом которого протяженность провода L в пролете ВЛ определяется уравнением параболы вида [11, с. 326].

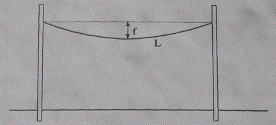
Рис. 2.15. Кривая провеса проводов

Приняв для ВЛ 10 кВ среднее расстояние между опорами около 70 м и мак­симальную стрелу провеса f до1,5 м, определим

что незначительно превышает длину пролета

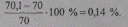
Более заметно увеличение расхода провода на монтажные концы и вязки, с учетом которых общий вес провода составит

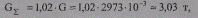
что практически совпадает с предыдущей оценкой.

ЗАДАЧА 2.4

Определить активное и индуктивное сопротивления ВЛ длиной 2,0 км с но­минальным напряжением 10 кВ, выполненной стальными проводами марки ПС 70, при токах нагрузки I, = 30 А и 1₂ = 150 А.

Провода расположены на одностоечных опорах по вершинам равностороннего треугольника, расстояние между проводами 1,0 м, диаметр провода d =11,5 мм.

Решение

Активное сопротивление Ro и внутреннее индуктивное сопротивление Х^”₀, соответствующие указанным токовым нагрузкам, определим по справочным дан­ным табл. П 1.8.

Внешнее индуктивное сопротивление Х'_о, зависящее от конструкции ВЛ, определяется по формуле (2.31).

При заданном расположении фазных проводов D_cp = D = 1,0 м получим

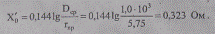
Расчет сопротивлений сведем в табл. 2.3.

Таблица 2.3 Изменение сопротивлений в зависимости от тока нагрузки

Проанализировав полученные результаты, можно сделать вывод: увеличе­ние токовой нагрузки в 5 раз сопровождается ростом сопротивления проводов ли­нии в 5,21/3,75= 1,39 раз.

ЗАДАЧА 2.5

Электроснабжение предприятия осуществляется по кабельной и воздушной ли­ниям напряжением 35 кВ (рис. 2.16), выполненных соответственно кабелем ОАБ 35×3×70 и проводом АС 70/11. Протяженность каждой линии составляет 10,0 км.

Определить и сопоставить параметры схем замещения кабельной и воздуш­ной линий электропередачи.

Рис. 2.16. Принципиальная схема электроснабжения

Решение

Из справочных данных табл. П 1.4 имеем следующие удельные (погонные) параметры для кабельной линии:

R_o =0,443 Ом/км, Х_о =0,137 Ом/км, q_o=86 квар/км.

Для воздушной линии по табл. П 1.14 имеем:

R_o= 0,428 Ом/км, Х_о= 0,432 Ом/км.

Определим параметры кабельной линии. Полное сопротивление

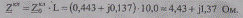
Удельную (погонную) емкостную проводимость рассчитаем по известному значению мощности q₀, квар/км при номинальном напряжении q_o=U²_ном*b₀ Отсюда погонная проводимость

и полная емкостная проводимость

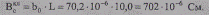
Результирующие параметры воздушной линии.

Полное сопротивление

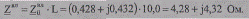
Удельную емкостную проводимость можно определить, используя данные D_ср для ВЛ 35 кВ по табл. П 1.3 для расположения проводов треугольником:

Полная емкостная проводимость

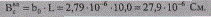
Сопротивления двух параллельно работающих линий характеризуются вы­сокой степенью неоднородности:

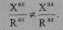
Определим параметры эквивалентной схемы замещения параллельно вклю­ченных линий (ВЛ и КЛ). С учетом одинаковой протяженности линий имеем

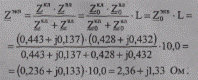
Эквивалентная проводимость линий

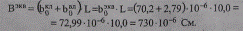
Проводимость В_с кабельной линии значительно превышает проводимость воздушной линии, что позволяет в итоге принять эквивалентное значение равным

Волновое сопротивление линий:

кабельной

воздушной

Натуральная мощность линий:

кабельной

воздушной

Оценим необходимость учета емкостной проводимости в схеме замещения ВЛ 35 кВ, сопоставив с проводимостью КЛ 35 кВ:

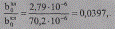
т. е. менее 4 % проводимости кабеля. Естественно, что в таком же соотношении находятся и зарядные токи (мощности) рассматриваемых линий. Ввиду незначи­тельности, значения зарядных (емкостных) мощностей ВЛ 35 кВ в справочных данных не приводятся. Так, значение емкостного тока воздушной линии 35 кВ

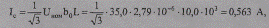
генерируемая линией зарядная мощность

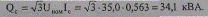
Для кабельной линии зарядную мощность можно определить по справоч­ным данным:

откуда емкостный ток

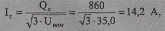
что больше аналогичных величин для ВЛ 35 кВ более чем в 25 раз. При сопоставлении зарядной мощности с натуральной имеем:

для КЛ 35 кВ

для ВЛ 35 кВ

Экономическая мощность кабельной и воздушной линии различается менее заметно, чем натуральная, и составляет для кабеля Р_э= 6,4 МВт [6, табл. 7.28].

Предельная экономическая нагрузка на одну цепь для ВЛ с проводом АС 70 рав­на I_э =75 А [6, табл.7.9]. Откуда

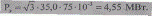
Следовательно,

для КЛ 35 кВ

для ВЛ 35 кВ

Таким образом, влияние емкостной проводимости и, соответственно, заряд­ной мощности на общее потокораспределение ВЛ 35 кВ незначительно и не пре­восходит ошибок исходных данных. Доля зарядной мощности КЛ 35 кВ в общей загрузке весьма ощутима. Такая мощность должна быть учтена в расчете режима линии. Поэтому схема замещения рассматриваемой электропередачи содержит емкостную проводимость только для кабельной линии (рис. 2.17).

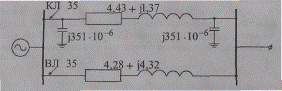
Рис. 2.17. Исходная схема замещения кабельной и воздушной линий 35 кВ

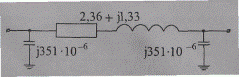
Рис. 2.18. Эквивалентная схема замещения кабельной и воздушной линий 35 кВ

Следовательно, и в эквивалентной схеме замещения линий (рис. 2.18) поперечная ветвь моделируется только проводимостью кабеля.

ЗАДАЧА 2.6

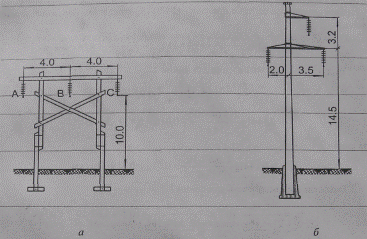
Электроснабжение района осуществляется по двум воздушным линиям 110 кВ с проводами марки АС 120/19. Одна линия выполнена на деревянных П-образных опорах с горизонтальным расположением проводов и расстоянием между проводами 4,0 м, другая линия смонтирована на унифицированных железобетонных опорах с расположением проводов по вершинам равнобедренного треугольника со сторонами 5,5; 3,2; 5,5 м (рис. 2.19).

Требуется сопоставить погонные параметры воздушных линий и опреде­лить эквивалентные параметры схемы замещения двух цепей длиной 100 км.

\

Рис. 2.19. Промежуточные опоры одноцепных линий напряжением 110 кВ:

а — деревянная, б — унифицированная железобетонная

Решение

Среднегеометрические расстояния между проводами линий составляют:

для первой линии (рис. 2.19, а) D_cр = 1,26·4,0 = 5,04 м,

для второй линии (рис .2.19, б) D_cp = 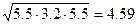м

По табл. П 1.9 и П 1.11 для значений D_cp= 5,0 м и D_cp= 4,5 м находим для провода марки АС 120/19 искомые параметры.

Для линии 1

R_o =0,270 Ом/км, Х_о =0,423 Ом/км, b₀=2,6910^-6 См/км;

для линии 2

R_o =0,270 Ом/км, Х_о =0,416 Ом/км, b₀=2,7410^-6 См/км.

Эти же параметры вычислим приближенно.

Активное сопротивление

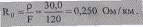
Уточним активное сопротивление. С учетом увеличения фактической длины из-за скрутки многопроволочных проводов и удлинения провода вследствие провиса до 5 %

Зная суммарное сечение провода АС 120/19, определяем наружный диаметр провода:

Индуктивное сопротивление для линии 1

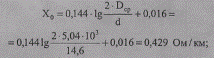
для линии 2

Емкостная проводимость для линии 1

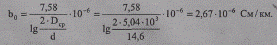
Емкостная проводимость для линии 2

Сопоставив погонные параметры при различном расположении фазных проводов на опорах с табличными значениями, отметим, что отличие составляет менее 2—3 % и не превышает погрешности исходных данных. Поэтому в практи­ческом инженерном анализе режимных показателей электрических сетей можно не учитывать исполнение ВЛ и принимать погонные параметры, характерные для данного класса напряжения.

Результирующие параметры схем замещения линии длиной 100,0 км опре­делим по выражению (2.1).

R₁ = R₂ = 0,270 • 100 = 27,0 Ом;

Х₁= 0,423 • 100 = 42,3 Ом;

Х₂ =0,416 • 100 = 41,6 Ом;

В₁ =2,69*10^-6 • 100 = 269*10^{-6 См;}

В₂=2,74*10^-6 • 100 = 274*10^{-6 См.}

Определим параметры эквивалентной схемы замещения (рис.2.20):

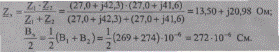
Суммарная емкостная проводимость линий определяет зарядную мощность

Сопоставим Q_c с натуральной мощностью двух ВЛ 110 кВ. Волновое сопротивление

где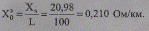

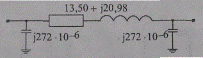
Рис. 2.20. Эквивалентная схема замещения двух ВЛ 110 кВ

Натуральная мощность

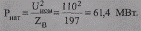
Зарядная мощность

соизмерима с натуральной мощностью и должна быть учтена при анализе режима ли­нии. Поэтому схема замещения рассматриваемой электропередачи должна включать активное и реактивное сопротивления и емкостную проводимость (рис. 2.20).

ЗАДАЧА 2.7

Определить, как изменятся погонные параметры и пропускная способность ли­нии электропередачи 220 кВ при горизонтальном расположении проводов и междуфазном расстоянии 7,0 м, если вместо провода АС 600/72 в каждой фазе подвесить два провода АС 300/48 с расстоянием между ними а_ср = 40 см (рис. 2.21).

Решение

1. Определяем среднегеометрическое расстояние между фазными проводами:

D_cp = 1,26 • D = 1,26 • 7,0 = 8,82 м.

По табл. П 1.9 и П 1.12 находим диаметр провода АС 600/72 2r_пр= 33,1 мм и погонные параметры нерасщепленной фазы R_o =0,055 Ом/км; Х_о =0,40 Ом/км;

b_о =2,8•10^-6 Ом/км.

Эти же параметры оценим аналитически.

Активное погонное сопротивление провода

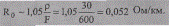
Индуктивное погонное сопротивление фазы

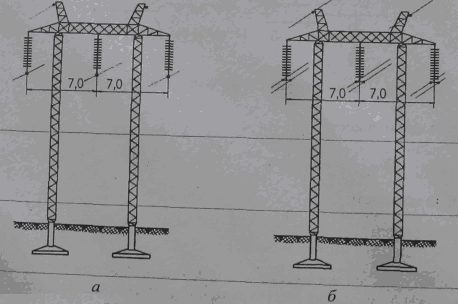
Риа 2.21. Промежуточные металлические опоры ВЛ 220 кВ-с нерасщепленной фазой (а) и с расщепленной фазой (б)

Полное погонное сопротивление провода

Z₀=R₀₊jX₀ =0,052 + j0,409 = 0,412 Ом/км

Погонная емкостная проводимость этого провода

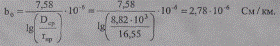
Волновое сопротивление линии

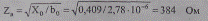
и ее натуральная мощность:

2. Рассчитываем погонные параметры фазы, расщепленной на два провода АС 300/48 (диаметр провода 2г_пр = 24,2 мм): активное сопротивление

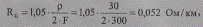
индуктивное сопротивление

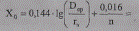
где эквивалентный радиус провода

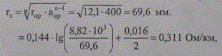
Полное удельное сопротивление

Емкостная проводимость

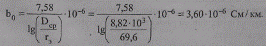
Полученные погонные параметры незначительно отличаются от значений, принятых по справочным данным табл. П 1.9иП 1.12:

R_o=0,054 Ом/км, Х_о=0,30 Ом/км, b_о=3,7-10^-6См/км.

Волновое сопротивление с расщепленной фазой

и натуральная мощность

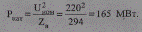
3. Сопоставим параметры линий. При расщеплении фазы на два провода по­гонное индуктивное сопротивление составит

т. е. на 24,0 % меньше, а погонная емкостная проводимость будет

т. е. увеличится на 29,5 %.

Расщепление фазы позволяет увеличить идеальный предел ВЛ 220 кВ по

передаваемой мощности:

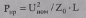
в соотношении

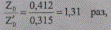
и натуральную мощность ВЛ 220 кВ в соотношении

Таким образом, расщепление фазы на два провода позволяет, не увеличивая суммарное сечение проводов, увеличить пропускную способность ВЛ 220 кВ примерно на одну треть.

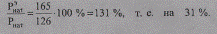
ЗАДАЧА 2.8

Определить параметры одноцепной воздушной линии напряжением 500 кВ, длиной 600 км, выполненной проводом марки АС 500/64.

Линия выполнена проводом марки АС 500/64 с расщеплением фазы на 3 провода. Расстояние между центрами расщепленных фаз по горизонтали 12,0 м, расщепленные провода расположены по вершинам равностороннего треугольника со стороной 40 см.

Линию представить:

1. Цепочной схемой замещения (рис. 2.9, а и 2.10, 6).

2. П-образной схемой замещения (рис. 2.9, в).

3. Пассивным четырехполюсником (рис. 2.9, б).

Решение

1. Определим параметры цепочной схемы замещения. Среднегеометрическое рас­стояние между центрами расщепленных фаз D_cp = 1,26·D = 1,26·12,0 = 15,12 м.

Из табл. П 1.9 находим диаметр провода 30,2 мм, погонное активное сопро­тивление

R₀ = 0,065 Ом/км.

Эквивалентный радиус расщепленной фазы

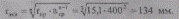
Погонные активное, индуктивное сопротивления и емкостная проводимость с учетом расщепления:

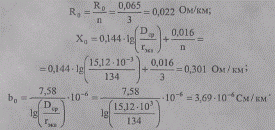
Протяженную ВЛ 500 кВ представляем цепочной схемой замещения с дву­мя звеньями (участками) длиной по 300 км, при которой отказ от учета распреде­ленности параметров не вызывает значительной погрешности в расчетах. Пара­метры каждого звена, моделируемого эквивалентной П-образной схемой замеще­ния, определим в виде

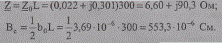
Потери активной мощности на корону по участкам схемы представим в ви­де нагрузки между участками. Приняв потери активной мощности при хорошей погоде около 10 кВт/км, получим нагрузки звеньев на корону:

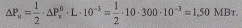
С учетом параметров каждого звена составим цепочную схему замещения в виде рис. 2.22.

2. Представление электропередачи П-образной схемой замещения.

При длине ВЛ свыше 300—350 км, необходим учет ее равномерной распределен­ности параметров. Удобно использовать поправочные коэффициенты (2.46):

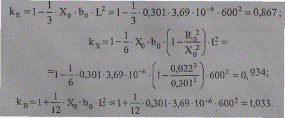
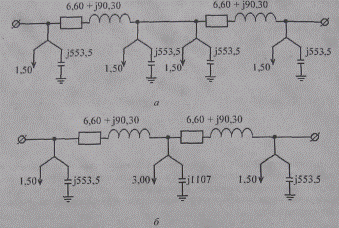
Рис. 2.22. Цепочная схема замещения ВЛ 500 кВ исходная (о), эквивалентная (б)

Тогда сосредоточенные параметры схемы замещения уточним по выражениям (2.47)

R = R₀Lk_R= 0,022·600·0,867 = 11,44 Ом;

X = X₀Lk_x =0,301·600·0,934 = 168,68 Ом;

B = B₀Lk_b =3,69·10^-6·600·1,033 = 2,29·10^{-3 См.}

Полные сопротивления и проводимости:

Z = R + jX = 11,44 + jl 68,68 = 169,07e^j86,12 Ом;

Y = jB = 2,29·10^-3e^j90 См,

используемые в П-образной или Т-образной схемах замещения ЛЭП.

3. Представление ЛЭП пассивным четырехполюсником с постоянными ко­эффициентами А, В, С, D.

Определим постоянные четырехполюсника по выражениям (2.38) и (2.41) на основании найденных параметров П-образной схемы замещения

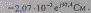
Постоянные четырехполюсника можно рассчитать и по уравнениям (2.36). Для этого необходимо определить волновые параметры линии. Волновое сопротивление

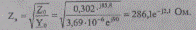
Коэффициент распространения электромагнитной волны вдоль линии

Отсюда коэффициент затухания β₀ =0,0387·10^-3 1/км, коэффициент фазы

α₀ =1,055·10^-3рад/км

Для удобства вычисления переведем радианы в градусы:

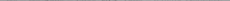
Натуральная мощность

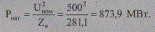
Гиперболические функции комплексного переменного:

Для линий до 1000 км можно принять, что 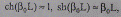тогда

Расхождение в значении констант, найденных двумя способами, находится в пределах погрешности исходных данных (< 3 %).