Выбор хранимых данных

Информационный фонд системы управления должен как минимум обеспечить получение выходных наборов данных из входных с помощью алгоритмов обработки и корректировки. Это возможно, если создана корректная инфологичесая модель предметной области. ИЛМ позволяет построить каноническую схему информационной базы, от нее перейти к логической схеме (даталогическая модель) и далее к физическому уровню реализации. Инфологической (концептуальной) моделью ПО называется такое ее описание, где не ориентируются на возможные программные и технические средства. Принципы построения ИЛМ известны. Однако для построения информационной базы одной ИЛМ недостаточно.

Необходимо провести анализ информационных потоков для установления связи между элементами данных. Нужно оценить их группировки в наборах входных, промежуточных и выходных данных, исключить избыточные связи и элементы данных. Получаемая в результате такого анализа безызбыточная структура называется канонической структурой информационной базы. Она является одной из форм представления ИЛМ. Для анализа информационных потоков в системе исходными являются данные о парных взаимосвязях, или отношениях (т.е.: есть отношения или нет отношений) между элементами или наборами элементов. Информационные элементы - различные типы входных, промежуточных и выходных данных, которые образуют соответствующие наборы:

1. N₁ - наборы входных элементов данных

2. N₂ - наборы промежуточных элементов данных

3. N₃ - наборы выходных элементов данных.

Формализовано связи (то есть парные отношения) между наборами информационных элементов представляются в виде матрицы смежности В. Матрица смежности - это квадратная бинарная матрица, которая проиндексирована по обеим осям множествам информационных элементов.

D={d₁, d₂, ...ds}, где s - число информационных элементов. Запишем матрицу В:

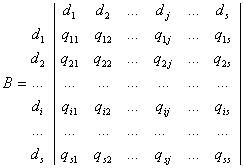
- qij=1, если между di и dj отношения существуют;

- qij=0, если не существуют;

- i= 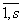; j= .

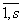В позиции ij матрицы смежности записывают 1(q_ij=1), если между информационными элементами d_j и d_i существует отношение R₀. R₀ таково, что для получения значения информационного элемента d_j необходимо обращение к элементу d_i. Наличие такого отношения между d_i и d_j обозначают: d_j R₀ d_i.Этому соответствует d_ji =1. Отсутствие отношения d_j R₀ d_i соответствует d_ji =0. При этом каждый информационный элемент недостижим из самого себя d_i= R₀ d_j (i= )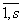

В соответствии с матрицей смежности существует информационный граф:G=(D;R₀) Множеством вершин графаG является множество D информационных элементов. Каждая дуга графа (d_i,d_j) соответствует условию d_g R₀d_i, то есть записи 1 в позиции ig матрицы В.

Пусть задано множество D из четырех наборов информационных элементов: D={d₁, d₂, d₃, d₄}. Пусть В имеет вид:

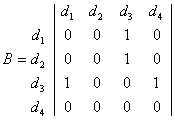
Из матрицы смежности видно:

1. для вычисления элемента d₃ необходимо обращение к элементамd₁ и d₂.

2. для получения элемента d₄ - обращаться только к d₃

3. элемент d₂ не зависит ни от одного из элементов матрицы.

В этом простейшем случае информационный граф соответствует рисунку:

При таком несложном варианте мы уже получили структуру информационных связей. Но если элементов существенно больше, воспринимать и анализировать такой граф крайне сложно, так как он неупорядочен. Граф составлен на основе ИЛМ, которая не гарантирует точности и неизбыточности.

Для формального выделения входных, промежуточных и выходных элементов, для определения последовательности операций обработки информационных элементов, для детального анализа взаимосвязей на основе графа G=(D, R₀) строят следующую матрицу - матрицу достижимости М. М достижимости - это квадратная матрица, проиндексированная по обеим осям множеством информационных элементов D. Запись=1 в каждой позиции (ij) соответствует наличию для каждой пары (d_i, d_j) смыслового отношения достижимости R. Существует ряд условий для построения матрицы М:

1. элемент d_j достижим из элемента d_i (то есть выполняется условие d_iRd_j), если на графе G=(D, R₀) существует направленный путь от вершины d_j к вершине d_i.

2. если d_iRd_j, то отношение достижимости между элементами d_i и d_j отсутствует и в позиции (ij) матрицы М записывают 0.

Разберемся, что дает нам структура матрицы М:

Запись "1" в j-том столбце соответствует информационному элементу d_i, который необходим для получения значений d_j. Они (записи) образуют множество элементов предшествования А(d_i) для данного элемента d_j.

Записи "1" в i-той строке матрицы М соответствуют всем элементам d_j, достижимым из рассматриваемого элемента d_i и образующим множество достижимостей R(d_i) этого элемента.

Отсюда можно сделать очень полезные выводы:

1. информационные элементы, строки которых в матрице М не содержат единиц (1), то есть нулевые строки, являются выходными информационными элементами.

2. информационные элементы, соответствующие нулевым столбцам матрицы М, являются выходными.

3. информационные элементы, не имеющие нулевой строки или столбца, являются промежуточными.

Для рассмотренного примера с простым графом с 4 элементами матрица достижимости М может быть записана:

М=

Отличие матрицы смежности В и достижимости М:

В матрице М учитывается смысловое отношение R между информационными элементами, а в матрице В учитывается только непосредственное R₀ - наличие отношений без учета их характера.

Информационный граф системы G_s(R) структурируется по уровням N₁, N₂, N₃. Он позволяет определить информационные входы и выходы системы, выделить основные этапы обработки данных, их последовательность, циклы обработки. При этом удаляются избыточные, лишние дуги графа и элементы , что наглядно видно на графе.

Выводы:

1. Граф, полученный после структуризации, определяет каноническую структуру информационной базы.

2. Каноническая структура задает логически неизбыточную информационную базу.

3. Выделение наборов данных по уровням объединяет логические записи и упорядочивает их в памяти.

От канонической структуры при описании процесса хранения переходят к логической структуре информационной базы. Логический уровень процедур хранения, актуализации и извлечения определяется моделями баз данных. Модели баз данных основаны на том, что структуры данных обладают устойчивостью. Взаимосвязи между информационными элементами могут быть типизированы основными видами:

- Один к одному.

- Один к многим.

- Многие к многим.

Применение одного из видов взаимосвязей определило три основные модели данных в БД .

Разработка модели процесса накопления данных должна выполняться в соответствии с предложенными этапами, что позволит эффективно реализовать один из важнейших информационных процессов в рамках ИТ:

1. Создание канонической структуры на основе инфологической модели предметной области и модели выбора хранимых данных.

2. Формализованное описание БД на основе трех моделей: модели хранения данных (структура БД), модели актуализации данных и модели извлечения данных.

3. На основе указанных моделей создаются алгоритмы и программы.

4. Создание физической модели происходит с помощью совокупности программ, реализуемых и используемых на ЭВМ .

Таким образом можно определить все этапы и все составляющие процесса накопления.