Модель процесса обработки

Внутримашинная обработка информации - это последовательно-параллельное во времени решение вычислительных задач. Такие процедуры возможны при наличии плана организации вычислительного процесса с учетом ресурсов данной ЭВМ. Источник вычислительных задач по мере необходимости обращается с запросом в ВС-вычислительную систему.

Организация вычислительного процесса - это определение последовательности решения задач и реализации вычислений. Последовательность определяется исходя из информационной взаимосвязи задач. Т.е. когда результаты решения одной задачи используются как исходные данные для решения последующей. Процесс решения задается вычислительным алгоритмом. В вычислительной системе можно выделить систему диспетчирования СД, отвечающую за организацию вычислительного процесса и саму ЭВМ, обрабатывающую информацию.

Каждая вычислительная задача может быть рассмотрена как заявка на обслуживание. Последовательность задач во времени создает поток заявок. Этот поток заявок можно формализовать (представить в виде математической модели) некоторым законом распределения времени обслуживания.

В теории массового обслуживания время обслуживания - это время, затраченное на обслуживание одной заявки конкретным обслуживающим прибором. В нашем случае этим прибором является ЭВМ.

В общем случае время обслуживания характеризуется определенным законом распределения:

F(t)=P(t_обс<t),
где P(t_обс<t) - вероятность того, что время обслуживания меньше t.

Время обслуживания реальной заявки на ЭВМ определяется числом операций, содержащихся в программе. Выясним, какими параметрами мы можем описать систему обслуживания задач в информационном процессе.

1. Состояние системы массового обслуживания в некоторый момент времени t определяется числом находящихся в ней заявок N(t). N(t) - это случайная величина.

Во времени N(t) отображает процесс с дискретными состояниями. Вероятность нахождения системы в состоянии "K" (K ¹N).

P_k(t)=P[N(t)=k] (17)

Рассмотрим последовательность переходов системы из одного состояния в другое состояние. Для этого выберем интервал U: t₁<U<t₂.

Тогда: 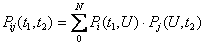, j£N; i³0,
где N- максимальное число заявок.

Можно составить систему таких уравнений для определения вероятностей P_k(t). Таким образом мы сможем описать все возможные переходы системы массового обслуживания. Но это только одна небольшая часть необходимых знаний о процессе обработки.

2. Время обслуживания системы - это следующий необходимый параметр. Время обслуживания тоже является случайной величиной и может быть определено разными законами распределения. Например, экспоненциальным законом времени обслуживания простейшего потока заявок. (Простейший - это стационарный поток без учета последствия).

Обозначим основной параметр потока l - интенсивность заявок, пусть - l = const. Простейший поток (стационарный без последствия) описывается распределением Пуассона:

Вероятность возникновения K заявок за время t составит:

,
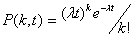где l - количество заявок за единицу времени, поток заявок.

Среднее число заявок за время t:

,
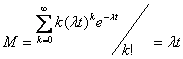М - это матожидание числа заявок за время t.

Т.о. в простейшем случае стационарного потока заявок без последействия не составит труда по описанным параметрам определить основные свойства вычислительного процесса.

В распределенной системе, если обслуживающих проборов, т.е. ЭВМ будет несколько, равных S, то тогда составим систему из S уравнений.

Но если процесс не стационарный и обслуживание последовательно-параллельное, все усложняется и для обслуживания заявок необходимо создавать целую структуру планирования вычислительного процесса.