Кристаллическая решётка

Кристаллическое строение твёрдых тел

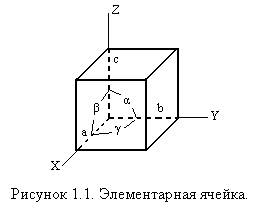
Структура твёрдого тела, состоящего из громадного количества атомов или молекул всегда упорядочена и регулярна. Это вызвано тем, что между отдельными частицами всегда существует взаимодействие, проявляющееся в наличии сил отталкивания и сил притяжения. Поскольку любая система стремится занять состояние, при котором она обладает минимумом энергии, то в твёрдом теле этот минимум достигается при равенстве сил отталкивания и притяжения, что достигается при вполне определённом расстоянии между каждой из частиц с соседними. В результате такого упорядочения частиц твёрдого тела его структура представляет собой кристаллическую решётку. Наиболее характерны периодические решётки, которые можно получить параллельным перемещением (трансляцией) частицы по трём осям в пространстве (трансляционные решётки Бравэ). При этом частица перемещается по оси Х на a, 2а, 3а,…, по оси Y – на b, 2b, 3b, …, по оси Z – на с, 2с, 3с,… Положение любой частицы определяется вектором r= ma+nb+pc, где a, b, c – основные векторы трансляции, m, n,р – целые числа.

Минимальный элемент пространства, образованный векторами трансляции a,b,c называется элементарной ячейкой. Элементарные ячейки (рис.1.1) все одинаковые, а в вершинах таких ячеек расположены одинаковые атомы или молекулы, поэтому все вершины эквивалентны друг другу и называются узлами ячейки. Основные векторы трансляции называются осевыми единицами в случае, если они являются единицам длины (т.е. все расстояния измеряются в осевых единицах, а не в абсолютных единицах длины – м, см, мм и т.д). Осевые единицы a, b, c вместе с углами между осями системы координат α, β, γ называются параметрами ячейки, таким образом, элементарная ячейка задаётся шестью параметрами – тремя линейными (a, b, c) и тремя угловыми (α, β, γ). Ещё следует отметить два обстоятельства – во первых, поскольку все ячейки эквивалентны, то начало координат может совпадать с любым произвольно выбранным узлом, а во – вторых, поскольку углы между осями являются параметрами ячейки, то системы координат могут быть самыми разными и прямоугольная является лишь частным случаем. Образование каким – либо элементом или соединением определённой пространственной решётки в основном зависит от размеров атомов и электронной конфигурации их внешних оболочек. Геометрически возможны лишь четырнадцать различных пространственных решёток, являющихся основой семи кристаллических систем: триклинная (a ≠ b ≠ c; α ≠ β ≠ γ ≠ 90º); моноклинная(a ≠ b ≠ c; α = γ =90º, β ≠ 90º); ромбическая(a ≠ b ≠ c; α = β = γ =90º); тетрагональная (a = b ≠ c; α = β = γ =90º); тригональная (a = b = c; α = β = γ ≠ 90º); гексагональная (a = b ≠ c; α = β = 90º, γ = 120º) и кубическая (a = b = c; α = β = γ = 90º).

Кристаллические тела, имеющие одинаковую геометрическую структуру могут отличаться по многим свойствам, что связано с наличием различных видов симметрии. Всего насчитывается 32 класса симметрии и 230 пространственных групп кристаллических решёток.

Твёрдые тела могут быть в виде отдельных крупных кристаллов (монокристаллы) или состоять из большого числа мелких кристаллов – зёрен (поликристаллы). В поликристаллах в пределах каждого зерна атомы составляют регулярную решётку, а на переходах от одного зерна к другому регулярность расположения частиц нарушается. В связи с этим большинство поликристаллических тел не обладают анизотропными свойствами в отличие от монокристаллов для которых как раз характерна анизотропия многих свойств. Промежуточным между монокристаллическим и поликристаллическим является блочное строение твёрдого тела, когда поликристаллы или монокристаллы соединяются в относительно крупные блоки. Так как многим твёрдым телам присуща анизотропия многих свойств (в том числе электрических и магнитных), то для описания этих свойств необходимо указывать расположение узлов, кристаллографических направлений и плоскостей. Для этого в кристаллографии введены понятия о индексах узлов, направлений и плоскостей.

Положение любого узла определяется заданием координат x, y, z; x = ma; y = nb; z = pc (a,b.c - параметры решётки; m, n, p – целые положительные или отрицательные числа). Если a,b.c - осевые единицы, то [[m n p]] – индексы узла (заключаются в двойные квадратные скобки).

Направления в кристалле (прямая, проведённая из начала координат) определяются индексами направлений, которые однозначно задаются индексами первого встреченного узла на этом направлении, т.е. индексы направлений задаются теми же числами [m n p], что и индексы узла, но для их различия индексы направления заключаются в одиночные квадратные скобки. Знак чисел m, n, p определяется относительно выбранного начала системы координат.

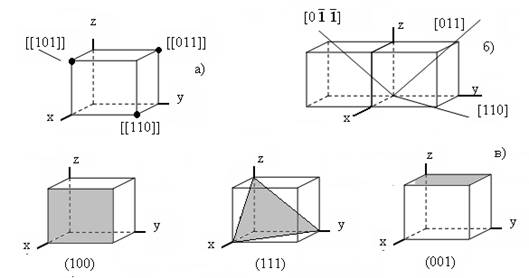
Рисунок 1.2. Индексы узлов (а), направлений (б) и плоскостей (в).

Плоскости в кристалле задаются индексами Миллера, суть которых можно определить следующим образом. Пусть некая плоскость в кристалле отсекает на осях выбранной системы координат отрезки m, n, p. Уравнение этой плоскости можно записать в виде x/m + y/n + z/p = 1. Приводя к общему знаменателю и освобождаясь от него, получим hx + ky + lz = D, где h, k, l – индексы Миллера (индексы плоскости). Обозначаются индексы плоскости в круглых скобках – (h k l). Очевидно, что h = np, k = mz, l = mn, D = mnp. Например, пусть m = 3; n = 2; p = 1. Уравнение плоскости x/3 + y/2 + z = 1; Приводим к общему знаменателю 2x + 3y + 6z = 6. Отсюда h = 2, k = 3, l = 6 и индексы Миллера для этой плоскости (2 3 6). Индексы Миллера обозначают совокупность параллельных плоскостей (в том числе и с отрицательными значениями индексов), так как параллельные плоскости имеют кратные координаты m, n, p.- 2m, 2n, 2p – 3m, 3n, 3p и т.д. и поэтому обозначаются одинаковыми индексами. Кристаллографически и физически эквивалентные плоскости обозначаются в фигурных скобках {h k l}, а физически эквивалентные направления – в угловых <m n p>. Индексы узлов, направлений и плоскостей позволяют определить целый ряд дополнительных параметров кристаллической структуры твёрдого тела. Это период идентичности – расстояние между одинаковыми (идентичными) атомами вдоль данного направления. Период идентичности зависит от всех параметров элементарной ячейки (a, b, c, α, β, γ). Для простой кубической решётки он легко вычисляется по очевидной формуле:

I = 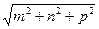. Другим параметром является межплоскостное расстояние так же зависящее от параметров ячейки. Для той же кубической решётки межплоскостное расстояние определяется по формуле:

.

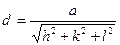Поскольку для других типов решёток осевые единицы и углы между ними не равны между собой, то формулы для вычисления периода идентичности и межплоскостных расстояний более сложные.