Дифракционная решетка

Дифракционная решетка представляет собой пространственную структуру, период которой соизмерим с длиной световой волны. Дифракционные решетки делят на пропускательные и отражательные. Простейшая пропускательная решетка представляет собой систему щелей в непрозрачном экране. Щели в такой решетке отстоят друг от друга на одном и том же расстоянии (рис. 10.4).

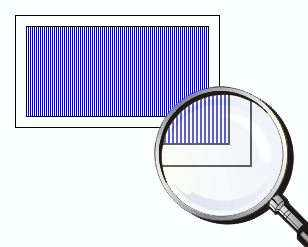
Дифракционная решетка

Рис.10.4

Расстояние d между серединами соседних щелей называется периодом решетки.

Отражательные решетки изготавливают путем нанесения штрихов на плоское или вогнутое зеркало или на металл.

Дифракционная решетка была изобретена в 1821г Фраунгофером. С 70х г.г. прошлого столетия была разработана новая технология изготовления дифракционных решеток, основанная на интерференции лазерного излучения. В результате интерференции двух лазерных пучков (см. рис 10.5), создается периодическое распределение интенсивности света в пространстве, которое записывается на специальном светочувствительном материале. Такого рода дифракционные решетки называются голографическими. Такие решетки делают для видимой и ультрафиолетовой областей спектра. Число штрихов,, нанесенных на один миллиметр, составляет от 600 до 6000.

рис.10.5

Период голографической решетки определяется следующим образом

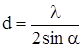
Период такой дифракционной решетки зависит от длины волны лазерного излучения и угла a между лазерными пучками, направленными на фотопластинку.

В спектральных приборах высокого класса вместо призм применяются дифракционные решетки. У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с 50 – 100 штрихами на миллиметр, нанесенными на поверхность прозрачной пленки. В качестве дифракционной решетки может быть использован кусочек компакт-диска или даже осколок граммофонной пластинки. Остановимся на пропускательной решетке и выясним характер дифракционной картины, получающейся на экране при падении на решетку плоской световой волны. На решетку направляется параллельный пучок исследуемого света. Наблюдение ведется в фокальной плоскости линзы, установленной за решеткой (рис. 10.6). Картины от всех щелей придутся на одно и тоже место на экране (независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку наблюдения не были когерентными, результирующая картина от N щелей, отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в N раз. Однако колебания от различных щелей являются в большей или меньшей степени когерентными; поэтому результирующая интенсивность будет отлична от NI_j (I_j— интенсивность, создаваемая одной щелью). Чтобы найти распределение интенсивности, даваемое дифракционной решеткой, найдем фазовые соотношения между колебаниями от различных щелей.

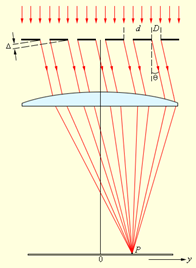
Рисунок 10.6 Дифракция света на решетке.

В каждой точке P на экране в фокальной плоскости линзы соберутся лучи, которые до линзы были параллельны между собой и распространялись под определенным углом θ к направлению падающей волны. Колебание в точке P является результатом интерференции вторичных волн, проходящих в эту точку от разных щелей (см опыт Юнга с учетом дифракции). Если угол дифракции равен нулю, то лучи, идущие от разных щелей соберутся в главном фокусе линзы. Они не имеют разности хода, следовательно, будут друг друга усиливать. В главном фокусе линзы формируется центральный максимум. Согласно рисунку 9.6, амплитуда волн, приходящих в точку Р от одной щели равна нулю, если выполняется условие (10.8). Так как все щели в этом случае в точке Р возбудят колебания с амплитудой равной нулю, то и результирующая амплитуда будет равна нулю. Поэтому условие минимумов для одной щели является и условием минимумов для дифракционной решетки:

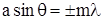(10.10)

это условие носит название условия главных минимумов. Для того, чтобы в точке P наблюдался интерференционный максимум, разность хода Δ между волнами, испущенными соседними щелями, должна быть равна целому числу длин волн:

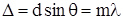(10.11)

Здесь d – период решетки, m – целое число, которое называется порядком дифракционного максимума. В тех точках экрана, для которых это условие (10.11)выполнено, разность фаз кратна 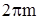и в этих точках располагаются так называемые главные максимумы дифракционной картины. Вследствие чего, амплитуда колебаний в соответствующей точке экрана равна 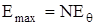, а интенсивность 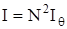. Таким образом, интенсивность главных максимумов в дифракционной картине от дифракционной решетки в N² раз больше интенсивности максимумов при дифракции от одной щели.