Броуновское движение

Молекулярно-кинетические свойства коллоидных систем можно исследовать, наблюдая броуновское движение, диффузию и осмос.

Броуновское движение проявляется в хаотическом и непрерывном движении частиц дисперсной фазы под действием ударов молекул дисперсионной среды (жидкости или газа), находящихся в состоянии интенсивного молекулярно-теплового движения. Оно наблюдается у любых мельчайших частиц и тем интенсивнее, чем выше температура и меньше масса частицы и плотность дисперсионной среды. Если крупные частицы перемещаются незначительно, то частицы коллоидной дисперсности, проявляя как поступательное, так и вращательное и колебательное броуновское движение, перемещаются в самых разных направлениях. Наблюдаемая траектория движения представляет собой ломаную линию совершенно неопределенной конфигурации (рис. 23.1). Перемещение частиц фиксируют, например, с помощью кинематографической микросъемки при наблюдении под микроскопом.

Крупные частицы при столкновении с молекулами окружающей среды получают импульсы, взаимно компенсирующие друг друга. Если же размеры частиц невелики, то

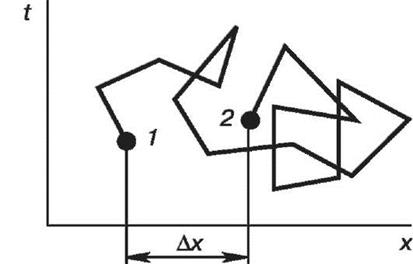Рис.Схема перемещения частицы при броуновском движении: Лх - величина смещения от точки 1 до точки 2; t - время

статистически всегда возможно, что за определенный интервал времени число ударов молекул или их интенсивность с одной стороны будут большими, чем с другой, в результате чего результирующая сила вызовет смещение частицы. Количественной мерой перемещения при броуновском движении является величина среднего смещения (или сдвига)

частицы ∆x за некоторый промежуток времени t. Смещением или сдвигом называют расстояние между проекциями начальной 1 и конечной 2 точек траектории на оси смещения х. Смещение одинаково вероятно как слева направо, так и в противоположном направлении, поэтому при вычислении среднего смещения за большой промежуток времени Ax может быть равно нулю. В связи с этим вычисляют среднюю квадратичную величину всех смещений без учета направления движения:

где n - число смещений (число отрезков ломаной линии); ∆xi - отдельные проекции смещения частиц на ось х. Согласно статистической теории броуновского движения, созданной А. Эйнштейном и М. Смолуховским в 1905-1906 годах на основании постулата о совершенной хаотичности движения, для сферических частиц среднее значение квадрата смещения ∆x²за время t равно:

где R - универсальная газовая постоянная; T - абсолютная температура; η - вязкость среды, r - радиус частиц; N_A- постоянная Авогадро; t - время.

Уравнение Эйнштейна-Смолуховского (23.2) подтверждает тот факт, что частицы перемещаются тем быстрее, чем выше температура, меньше размер частиц и вязкость среды. В частности, с увеличение размера частиц, прежде всего, прекращается поступательное броуновское движении, затем исчезает вращательное движение и остается только колебательное.

При изучении броуновского движения было открыто явление флуктуации в распределении частиц, что явилось важным шагом в развитии статистических методов исследования.

Диффузия

Диффузией называют самопроизвольное движение частиц среды, приводящее к переносу вещества и выравниванию концентраций или установления равновесного распределения концентраций частиц данного сорта в данной среде.

Диффузия свойственна как молекулярным, так и коллоидным растворам, и может осуществляться за счет броуновского движения. Броуновское движение хаотично и беспорядочно, но если в системе имеются участки с различной концентрацией частиц, то суммарное число смещений будет всегда больше со стороны участка с высокой концентрацией и высоким химическим потенциалом в сторону участка более разбавленного и с меньшим химическим потенциалом. На рис. 23.2 представлена схема процесса диффузии и изменение концентрационных профилей при перемещении частиц из объема с исходной концентрацией с (рис. 23.2, кривая 1, t = 0) в объем чистой дисперсионной среды. Кривые изменения концентрации в направлении х показывают распределение частиц в системе в различные моменты времени t. Естественно, что наибольшие изменения концентрации dc/dx наблюдаются вблизи начальной границы раздела АВ. По окончании определенного времени (рис. 23.2 , кривая 5, t =∞) в системе устанавливается равновесие, характеризуемое равенством химического потенциала и концентрации частиц по всему объему системы.