Свойства выборочного коэффициента корреляции
1. Коэффициент корреляции является безразмерной величиной и его значение не зависит от единиц измерения признаков 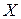 и
и 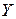 . Коэффициент линейной корреляции принимает значения на отрезке от (-1) до (+1), т.е.
. Коэффициент линейной корреляции принимает значения на отрезке от (-1) до (+1), т.е.
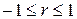 . (6.2)
. (6.2)
2. Направление взаимосвязи. Если 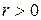 , то корреляционная связь между переменными положительная: большему значению одной переменной соответствует в среднем большее значение другой переменной. Если
, то корреляционная связь между переменными положительная: большему значению одной переменной соответствует в среднем большее значение другой переменной. Если 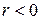 , то корреляционная связь между переменными отрицательная: большему значению одной переменной соответствует в среднем меньшее значение другой переменной.
, то корреляционная связь между переменными отрицательная: большему значению одной переменной соответствует в среднем меньшее значение другой переменной.
3. Форма связи. По форме зависимость признаков может быть линейной или нелинейной. Если коэффициент линейной корреляции Пирсона по модулю близок к 1, то это соответствует высокому уровню линейной связи между переменными.
4. Теснота связи. В зависимости от того, насколько 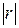 приближается к 1, различают сильную, умеренную и слабую связь.
приближается к 1, различают сильную, умеренную и слабую связь.
Если коэффициент корреляции по абсолютной величине больше 0,95, то принято считать, что между переменными существует тесная линейная зависимость.
Если величина 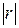 лежит в диапазоне от 0,7 до 0,95, то говорят о сильной линейной связимежду переменными.
лежит в диапазоне от 0,7 до 0,95, то говорят о сильной линейной связимежду переменными.
Если 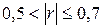 , говорят о средней линейной связи.
, говорят о средней линейной связи.
Если 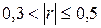 , говорят об умеренной линейной связи.
, говорят об умеренной линейной связи.
Если 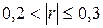 , говорят о слабой линейной связи.
, говорят о слабой линейной связи.
При 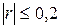 считают, что линейная связь очень слабая или линейную взаимосвязь между переменными выявить не удалось.
считают, что линейная связь очень слабая или линейную взаимосвязь между переменными выявить не удалось.
При значении коэффициента корреляции, очень близком к 0, линейная связь между двумя выборками отсутствует, но может быть нелинейная форма корреляционной связи.
Дата добавления: 2016-11-26; просмотров: 2919;











