Тема 5. Ротационные реометры
Совокупность объектов реологических исследований охватывает широкий диапазон агрегатных состояний материалов, начиная от твёрдых тел и кончая маловязкими жидкостями. Это, а также разнообразие целей реологических исследований, требует применения исключительного разнообразия приборов, как по принципу действия, так и по конструктивным особенностям.
Принцип ротационных реометров с измерительными ячейками типа коаксиальных цилиндров, конус-плоскость и плоскость-плоскость позволяет конструировать разнообразные реометры.
В реометрах применяются два основных варианта геометрии измерительных систем, которые позволяют:
А – задавать напряжение и определять полученную в результате величину скорости сдвига; эти приборы называют “реометрами с контролируемым напряжением, или CS-реометрами”;
Б – задавать скорость сдвига и определять полученное в результате этого напряжение сдвига; эти приборы называют “реометрами с контролируемой скоростью сдвига, или CR-реометрами”.
Некоторые современные реометры могут работать в обоих режимах испытаний. Но они обладают другим дополнительным техническим отличием, а именно: они снабжены измерительными системами Серле (1) или Куэтта (2) (рис. 16).
А 1 — CS-реометр, основанный на принципе Серле, с измерительными ячейками типа коаксиальные цилиндры, конус-плоскость и плоскость-плоскость.Принцип Серле заключается в том, что внешний цилиндр (стакан) неподвижен и в нем можно задавать определенную температуру с помощью рубашки или внешней термостатирующей бани, в которых циркулирует теплоноситель, подаваемый из термостата.
Внутренний цилиндр, ротор, вращается специальным мотором М. Момент вращения на валу мотора может быть предварительно задан: он линейно зависит от поданной электроэнергии. Сопротивление образца, помещенного внутри измерительной ячейки, крутящему моменту или напряжению сдвига позволяет ротору вращаться только при такой скорости (скорости сдвига), которая обратно пропорциональна вязкости данного образца.
Принцип Серле в данном контексте означает, что крутящий момент передается непосредственно на вал ротора, скорость вращения которого подлежит измерению. Измерительные системы устроены таким образом, что крутящий момент может быть пересчитан в напряжение сдвига, а частота вращения ротора - в скорость сдвига.
Измерительные системы могут быть модифицированы таким образом, что наружный цилиндр заменяется на стационарную нижнюю плоскость, а внутренний цилиндр - на вращающиеся конус или плоскость. Измерение вязкости заключается в предварительном задании вращающего момента, измерении полученной частоты вращения ротора, оценки по этим данным напряжения и скорости сдвига, после чего рассчитывают соответствующую вязкость.
Б1 - CR-реометры, основанные на принципе Серле, с измерительными системами типа коаксиальные цилиндры, конус-плоскость или плоскость-плоскость. Внутренний цилиндр (ротор) вращается двигателем М с постоянной или изменяющейся по программе скоростью, в то время как внешний цилиндр (стакан) неподвижен. Стакан снабжен рубашкой для точного термостатирования измеряемого образца. Движение внутреннего цилиндра приводит к течению жидкости, находящейся в кольцевом зазоре между внутренним и внешним цилиндрами. Сопротивление жидкости, которая подвергается сдвигу между неподвижной и движущейся поверхностями измерительной системы, приводит к возникновению на внутреннем цилиндре крутящего момента, связанного с вязкостью жидкости и направленного против крутящего момента двигателя. Индикатор крутящего момента (обычно это пружина, которая закручивается под влиянием приложенного крутящего момента) расположен между валом двигателя и валом внутреннего цилиндра. Угол закручивания пружины является прямой мерой вязкости образца. Принцип Серле и в этом случае означает, что как привод ротора, так и датчик крутящего момента связаны с одной и той же осью ротора.
Возможность легкого изменения геометрии измерительных систем (коаксиальный цилиндр, конус-плоскость или плоскость-плоскость) позволяет использовать этот тип реометра для измерения средних или очень высоких значений вязкости жидкостей. При пользовании реометром типа Серле возникает проблема с измерениями вязкости низковязких жидкостей при высоких скоростях сдвига, так как при этих условиях ламинарное течение может переходить в турбулентное, что приводит к неправильным результатам.
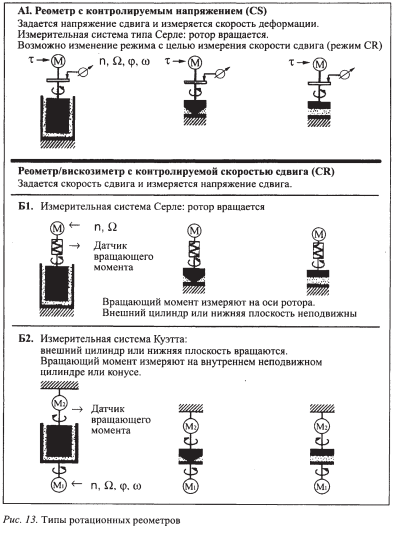 Рис. 16. Типы ротационных реометров
Рис. 16. Типы ротационных реометров
Б2 - CR-реометры, основанные на принципе Куэтта, с измерительными узлами типа коаксиальные цилиндры, конус-плоскость или плоскость—плоскость. В этом случае в отличие от предыдущего внешний цилиндр вращается с определенной скоростью двигателем Ml. Термостатирование внешнего цилиндра технически сложно и достаточно дорого. Вращение внешнего цилиндра вызывает течение жидкости в кольцевом зазоре. Из-за сопротивления жидкости, подвергаемой сдвигу, крутящий момент, пропорциональный вязкости жидкости, передается на внутренний цилиндр и также должен вызвать его вращение. Этот крутящий момент определяют, измеряя противодействующий крутящий момент, необходимый для того, чтобы внутренний цилиндр оставался неподвижным.
В конструкции куэттовского типа движущее усилие прикладывают к внешнему цилиндру, а крутящий момент, связанный с вязкостью, измеряют на валу внутреннего цилиндра – другого элемента измерительной системы.
В данном случае вместо пружины, как отмечено в разделе В1, датчиком крутящего момента служит двигатель М2, соединенный с валом внутреннего цилиндра или конуса. С помощью этого двигателя создается контролируемый крутящий момент, равный по величине, но противоположный по направлению наведенному и препятствующий вращению внутреннего цилиндра, конуса или верхней плоскости. При таком компенсационном методе измерений мощность, потребляемая вспомогательным двигателем М2, является величиной, связанной с вязкостью.
В измерительных системах куэттовского типа сохраняется ламинарный режим течения даже в том случае, когда низковязкие жидкости испытывают при высоких скоростях сдвига. Именно в этой области они превосходят CR-реометры типа Серле.
Сравнение CS- и CR-реометров
Конструкция CS-реометров позволяет расширить измеряемую область скорости сдвига до 10-4 или даже до 10-6 с-1, при которой могут быть достоверно определены крутящий момент (а значит, напряжение сдвига) и, соответственно, вязкость. Самая низкая скорость сдвига CS-реометров распространяется на много десятичных порядков ниже области, доступной CR-реометрам (рис. 17).
а) Большинство CS-реометров сконструированы таким образом, чтобы обеспечить наиболее высокую чувствительность и выявить различия между подобными образцами при очень низких скоростях сдвига, при которых более простые вискозиметры не могут дать удовлетворительных результатов.
10-6 10-4 10-2 100 102 105
Скорость сдвига (1/с)
Рис. 17. Диапазоны скоростей сдвига при различных режимах измерений.
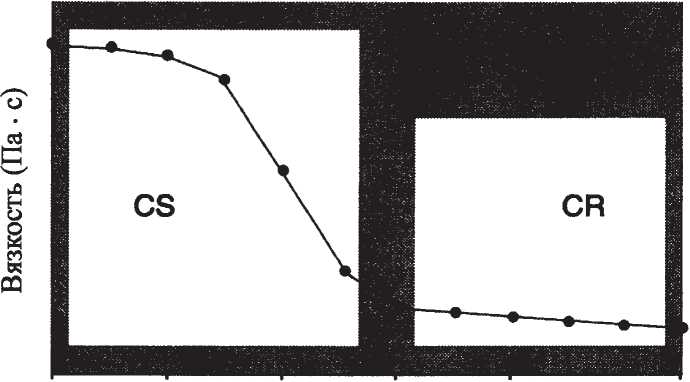
Различные типы полимерных расплавов, различающиеся молекулярной структурой, дают кривые зависимости вязкости от скорости сдвига, которые располагаются гораздо ближе друг к другу при высоких скоростях (рис.18).
Анализ этих трех кривых приводит к заключению, что измерения не только для расплавов ПММА, но и для других подобных между собой полимерных расплавов предпочтительнее проводить при низких скоростях сдвига, чтобы эффективнее выявить различия между ними.
Это соображение подтверждается как значением отношения вязкостей (полимер N1 –η1,полимер N3 –η3), так и значением их разности при высоких (1000 с-1) и низких (1 с-1) скоростях сдвига:
при  = 1000 с-1
= 1000 с-1 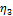 /
/ 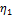 =500/200 = 2,5
=500/200 = 2,5
при  = 1 с-1
= 1 с-1 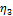 /
/ 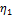 =57000/1800=31,6
=57000/1800=31,6
при  = 1 с-1
= 1 с-1 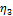 -
- 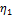 = 57 000 -1800 = 55 200
= 57 000 -1800 = 55 200
при  = 1000с-1
= 1000с-1 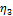 -
- 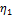 = 500-200 = 300
= 500-200 = 300
Аналогично можно привести значения отношения и разности напряжений сдвига при низких и высоких скоростях сдвига:
при  = 1
= 1 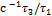 =45 000/1700 = 26,4
=45 000/1700 = 26,4
при  = 1000 с-1
= 1000 с-1 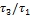 =45000/200000 = 2,25
=45000/200000 = 2,25
при  = 1 с-1
= 1 с-1 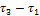 = 45000-1800 = 43 200
= 45000-1800 = 43 200
при  = 1000 с-1
= 1000 с-1 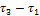 = 45 0000 - 20 000 = 25 0000
= 45 0000 - 20 000 = 25 0000
Разность напряжений сдвига значительно выше при высоких скоростях сдвига, чем при низких, и отсюда можно заключить, что разрешение измерений вязкости выше в области высоких скоростей сдвига.
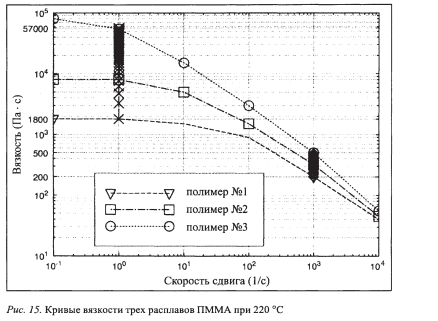
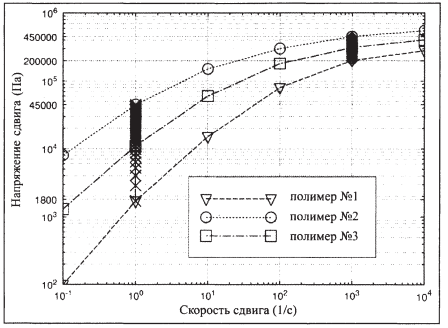
Рис. 18. Кривые вязкости и течения трех расплавов полиметилметакрилата.
б) CS-реометры превосходят CR-реометры при испытаниях жидкостей, характер течения которых сильно отличается от ньютоновского.
Поведение многих полимерных расплавов и дисперсий существенно отличается от ньютоновского, т.е. рост скорости сдвига не приводит к пропорциональному увеличению напряжения сдвига, как это имеет место в случае ньютоновских жидкостей. Например, если для ньютоновской жидкости увеличение скорости сдвига на три десятичных порядка приводит к такому же возрастанию напряжения сдвига (рис. 19), то для неньютоновской жидкости (например, расплава ПММА) при возрастании γ на три порядка τ возрастает всего лишь на порядок – от 45000до 450000Па.
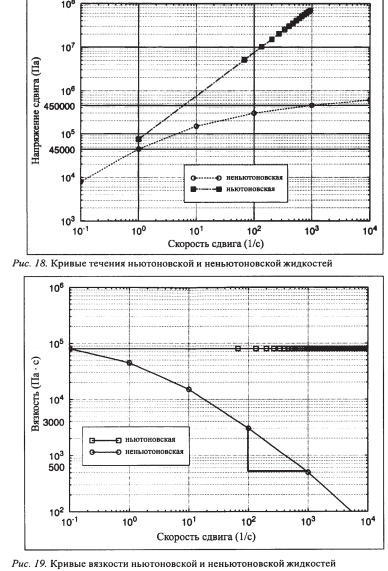

Рис. 19. Кривая течения и вязкости ньютоновской и неньютоновской жидкости.
Зависимость вязкости ньютоновской жидкости от скорости сдвига представляет собой прямую, параллельную оси абсцисс, т. е. вязкость не зависит от скорости сдвига, в то время как вязкость расплава ПММА снижается от 3000 до 500 Па с при увеличении скорости сдвига на десятичный порядок.
в) CS-реометры превосходят CR-реометры при испытаниях образцов определенного реологического поведения, а именно таких, которые проявляют характер течения, свойственный как твердому, так и вязкому телу в зависимости от скорости сдвига и сдвиговой предыстории.
На схематической кривой течения материала, обладающего пределом текучести, снятой с помощью CS-реометра (рис. 20), показано возрастание напряжения вдоль оси ординат (при скорости сдвига, равной нулю). При достижении предела текучести кривая течения резко отклоняется от оси ординат и далее монотонно возрастает с увеличением скорости сдвига.
Реальная картина в случае CS-реометра выглядит следующим образом. Прикладывая к образцу контролируемое напряжение сдвига, мы не можем измерить какую-либо реальную скорость сдвига до тех пор, пока напряжение не увеличится настолько, чтобы преодолеть сопротивление образца, который ведет себя как твердое тело. Образец “схватывает” ротор и удерживает его в неподвижном положении. После превышения предела текучести ротор начинает вращаться и его отклонение очень точно фиксируется особо чувствительным датчиком деформации (рис. 20, черные точки). Таким образом, реализуется возможность правильного определения характера течения дисперсий, отличающихся малыми значениями пределов текучести.
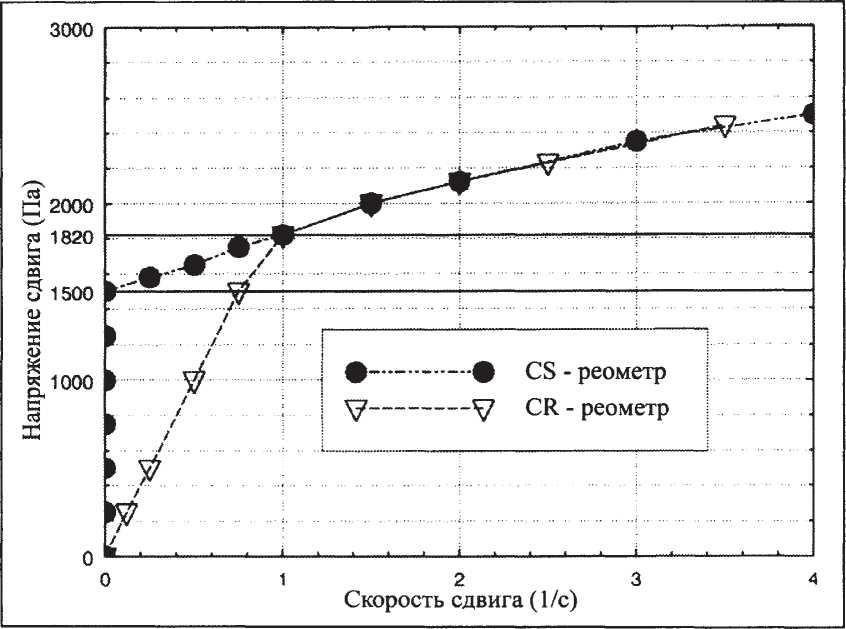
Рис. 20. Сравнение CS- и CR-реометров при измерении предела текучести.
Принцип действия большинства CR-реометров, обычно технически менее сложных и более дешевых, чем CS-реометры, иной.
Электрический двигатель, связанный с тахометром-генератором, задает скорость вращения ротора. Вращение передается на внутренний цилиндр – ротор, который в случае системы коаксиальных цилиндров погружен в измеряемый образец. Торсионный датчик угла поворота ротора (мягкая пружина, работающая на скручивание, у которой полному диапазону крутящего момента соответствует отклонение примерно в 90°) расположен между ротором и двигателем. Вращение ротора в жидкости создает заданный градиент скорости сдвига; в то же время из-за сопротивления образца сдвигу возникает противодействующий крутящий момент, пропорциональный вязкости, который, соответственно, закручивает торсионный датчик.
Это значит, что при испытании образца, обладающего пределом текучести, двигатель начинает медленно вращаться и его скорость определяется тахометром-генератором в виде электрического сигнала. Но ротор, будучи окружен твердообразным образцом, удерживается в состоянии, обусловленном только моментом скручивания пружины. В вискозиметрах с мягкой пружиной в области измерений ниже предела текучести действительные скорости двигателя и ротора существенно различаются. Кривая течения в координатах напряжение сдвига - скорость сдвига имеет вид наклонной прямой. Угол этого наклона соответствует “коэффициенту пружины”, т.е. ее упругости, но никоим образом не отражает свойств материала. В начале кривой течения регистрируемая скорость сдвига не явяется фактической скоростью сдвига в слое образца, а только отражает сигнал вращения двигателя и тахометра-генератора (рис. 20, треугольные точки). С увеличением скорости вращения двигателя напряжение внутри образца, подвергаемого сдвигу, возрастает, и наступает момент, когда оно превышает предел текучести образца. С этого момента ротор действительно начинает вращаться и скорость его вращения почти моментально достигает скорости вращения двигателя. С началом реального течения образца кривая течения круто изменяет свой наклон, и с этого момента увеличение скорости вращения двигателя и ротора становится идентичным и может быть использовано для расчета соответствующей скорости сдвига. Напряжение сдвига в точке резкого изменения наклона кривой течения определяют как предел текучести исследуемого образца.
Таким образом, CS- реометры по сравнению с CR-реометрами/вискозиметрами дают возможность более широкого и глубокого проникновения во внутреннюю структуру полимеров и позволяют измерять характеристики, имеющие существенное значение при их переработке.
Рассмотрим достоинства и недостатки различных типов измерительных систем.
Измерительная система типа коаксиальных цилиндров.
Проверенная временем, простая и надежная конструкция, имеющая тем не менее по крайней мере 2 недостатка. Во-первых, измерительная система требует достаточно большого объема исследуемого образца. А во вторых, при данной конструкции существует ошибка при определении скорости сдвига.
Уравнение скорости сдвига в случае коаксиальных цилиндров аппроксимируют простым уравнением
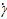 =
= 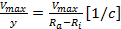
Это справедливо в случае модели параллельных плоскостей и ньютоновских жидкостей. После изгиба этих плоскостей и придания им формы стакана и ротора градиент скорости поперек зазора у = Ra – Rii становится нелинейным. Если просто разделить Vмакс на у, чтобы рассчитать соответствующую скорость сдвига не только для условий вблизи поверхности ротора, но и для любой точки между Ra и Ri то нужно учесть погрешность, зависящую от размера зазора. Эта погрешность представлена на рис. 21 в виде двух затушеванных областей между предполагаемым линейным и реальным нелинейным градиентами скорости поперек зазора. Градиент скорости станет еще более нелинейным, если перейти от ньютоновской жидкости к неньютоновской.
Данная погрешность может быть сведена к минимуму уменьшением размера зазора, что приводит к линеаризации градиента скорости поперек зазора.
Для определения углового размера зазора вместо разности радиусов Ra – Ri обычно используют отношение радиусов:
δ = Ra/Ri
Это отношение в реальных измерительных системах ротационного реометра всегда больше 1,00. Отношение 1,00 было бы возможным, только если бы оба радиуса были одинаковы, а зазор сократился бы до нуля. С точки зрения реологии, чем ближе это отношение к 1,00, тем лучше. Отношение 1,10 при одинаковой частоте вращения ротора п уже приводит к скорости сдвига, почти на порядок меньшей, чем при Ra/Ri= 1,01, а соответствующие значения вязкости различаются на 37%. Ввиду того что отношение радиусов имеет существенное значение для точности измерений вязкости неньютоновских жидкостей, в международном стандарте Германии введены такие ограничения:
1,0 ≤δ ≤1,10.
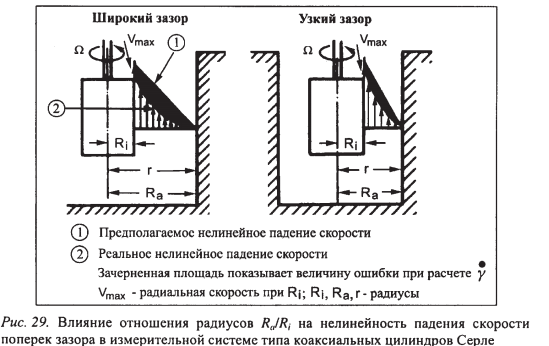
Рис. 21. Влияние отношения радиусов на нелинейность падения скорости поперек зазора.
Измерительные системы конус – плоскость. Применение конуса с малым углом дает прекрасное качество результата испытаний. Измерительные системы конус-плоскость изготавливают в основном с углом конуса a = 0,0174 рад (1°). При этом необходимо учитывать возможность возникновения больших ошибок в результатах измерений в тех случаях, когда контакт между конусом и плоскостью либо плохо установлен, либо не поддерживается стабильным, а также при неконтролируемом изменении температуры образца при высокой скорости сдвига.
Эти измерительные системы часто выбирают в тех случаях, когда затруднена очистка поверхности измерительного узла после проведения испытаний. При необходимости очень большого количества измерений в день, например при контроле качества дисперсий с высоким содержанием пигмента, очистка стакана и ротора цилиндрической измерительной системы гораздо труднее и требует больше времени, чем очистка легко доступной системы конус-плоскость.
Важным аргументом в пользу выбора этой измерительной системы часто является то, что в данном случае, как правило, количество образца, необходимое для измерений, гораздо меньше того, которое требуется для большинства цилиндрических измерительных систем. Это имеет значение, когда образец либо очень ценный, либо его очень мало, всего несколько капель. Объем образца зависит от угла конуса и его радиуса
| Диаметр, мм | 17,5 | |||
| Угол конуса, град | ||||
| Объем, см3 | 0,02 | 0,2 |
Измерительные системы конус-плоскость применяются в основном при высоких скоростях сдвига, вплоть до  = 104 с-1.
= 104 с-1.
Однако, измерительные системы конус-плоскость в большей мере, чем цилиндрические измерительные системы, подвержены влиянию нормальных напряжений, которые возникают в результате упругих реакций вязкоупругих образцов, подвергаемых сдвигу. Эти нормальные напряжения способны вытягивать элементы объема испытуемого образца из углового зазора и поднимать их вверх по внешнему краю конуса. Это серьезное нарушение режима измерения вязкости.
Измерительные системы типа плоскость-плоскость. Эти системы в какой-то мере альтернативны измерительным системам конус-плоскость. Они требуют несколько большего объема образца, чем системы конус-плоскость с таким же радиусом конуса, но все же их объем составляет малую долю от объема нормальных измерительных систем типа коаксиальных цилиндров. Для них не существует проблемы с образцами, содержащими крупные агрегаты наполнителя. Сдвиговый зазор этих измерительных систем легко наполнять образцом, обладающим высоким пределом текучести, так как при установке конечного размера зазора между пластинами не происходит сколько-нибудь значительного радиального сжимающего течения в образце до начала его испытания.
Измерительные системы типа плоскость-плоскость широко применяют в современных CS-реометрах для испытания большинства образцов, обладающих вязкоупругими свойствами. В то время как измерительная система конус-плоскость с малым углом конуса очень подходит для измерения вязкости неньютоновских жидкостей, система плоскость-плоскость с широким измерительным зазором (примерно 2 мм) является идеальной для измерения упругости твердообразных и вязкоупругих жидкостей.
Дата добавления: 2016-11-04; просмотров: 7055;











