Проведем простой опыт для доказательства того, что ток, получаемый от электростанций, действительно переменный (постоянно меняющий свое направление).

Включим в сеть обыч­ную электрическую лампочку и осторожно поднесем к ней постоянный магнит так, чтобы нить лампочки была пер­пендикулярна к линии его магнитного поля. Мы увидим, что при этом нить лампочки расплывается в широкую полоску. Это показывает, что нить в поле магнита быстро колеблется, отклоняясь, то в одну сторону, то в другую. Но мы знаем, что в постоянном магнитном поле ток опре­деленного направления отклоняется в одну сторону. Сле­довательно, наш опыт показывает, что ток в нити лам­почки меняет свое направление много раз в секунду.

Этот простой опыт, хотя показывает нам, что ток в сети – переменный, но не дает еще возможности проследить за законом изменения мгновенных значений силы тока, т.е. изучить его форму. Если бы мы в своем первоначальном опыте вращали рамку достаточно медленно, то увидели бы, что стрелка гальванометра во внешней цепи рамки отклоняется то в одну сторону, то в другую. Учитывая эти отклонения, мы могли бы составить представление о форме тока, но переменный технический ток меняет направление настолько часто, что обычные гальванометры не успевают следить за его изменениями. Поэтому нужны более чувствительные приборы, которые получили название осциллографы. Осциллографы – это приборы, предназначенные для исследования быстропеременных токов и напряжений. Опыт, проведенный с использованием осциллографа, показывает, что для технического тока кривая, изображающая форму переменного тока, действительно очень близка к синусоиде. Такой же вид имеют и кривые, изображающие форму технического переменного напряжения.

1.5. Рассмотрим теперь индуктивность катушки. При самоиндукции, как и при всяком процессе индукции, индуцированная в ка­тушке э. д. с. пропорциональна скорости изменения маг­нитного потока через витки катушки. Магнитный же поток пропорционален силе тока в цепи.

Если в некоторый момент t₁сила тока в цепи равна i₁, то магнитный поток Ф₁ будет пропорционален i₁, т.е.

Ф₁ = Li_1,

где L — коэффициент пропорциональности, зависящий от числа витков, размеров и формы катушки и, следовательно, имеющий различные значения для различных катушек. Пусть через небольшой промежуток времени, к моменту t₂, сила тока в цепи стала равной i₂ и, следовательно, в этот момент магнитный поток

Ф₂ = Li₂.

Таким образом, за время t₂—t₁ магнитный поток изме­нился на Ф₂—Ф₁ = L(i₂—i₁).Обозначив, как и прежде, небольшие разности Ф₂—Ф₁, i₂—i₁, t₂—t₁ соответственно через DФ, Di, Dt,найдем э. д. с. индукции с помощью соотношения

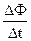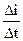x₁ = = L . (1)

Характеризующий катушку множитель L называется индуктивностью катушки. Если катушка такова, что при изменении тока на Di=l А в течение времени Dt=1 с в цепи возникает э. д. с. x = 1 В, то индуктивность подоб­ной катушки принимают за единицу для измерения ин­дуктивности. Эта единица получила название генри (Гн) в честь американского физика Джозефа Генри (1797— 1878). Таким образом, если измерять индуктивность катушки в генри, ток в амперах, а время в секундах, то э. д. с. самоиндукции выразится с помощью формулы (1)в вольтах. Если, например, индуктивность катушки равна 5 Гн и ток в ней изменяется на 1 А за 0,02 с, то сред­няя индуцированная э. д. с.

x₁ = 5 Гн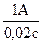^. = 250 В.

Расчеты и эксперимент дают, что индуктивность очень длинной катушки (соленоида) определяется формулой

L = mm_{0 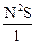,} (2)

где N — число витков, S — площадь сечения, l — длина катушки, m— относительная магнитная проницаемость среды, заполняющей катушку. Таким образом, индуктив­ность катушки тем больше, чем больше площадь ее сече­ния, ибо это условие увеличивает магнитный поток через катушку при одном и том же токе в ней. Если вставить в катушку железный сердечник, индуктивность ее сильно возрастает, так как относительная магнитная проницаемость железа очень велика. В соответствии с формулой (2)

m₀ = ,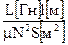

откуда следует, что m₀ может быть выражена в генри на метр (Гн/м) . Напомним, что m и N — безразмерные величины.

Явление индукции, а следовательно, и самоиндукции происходит не только в катушках, но и в проводниках любой формы, в том числе и в прямолинейных проводниках. Поэтому любой проводник характери­зуется определенным значением индуктивности. Однако для большин­ства проводников, не имеющие формы катушки, индуктивность настоль­ко мала, что обычно на самоиндукцию в таких проводниках можно не обращать внимания. Только при очень быстрых изменениях тока, когда отношение Di/Dt становится очень большим, приходится считаться с э.д.с. самоиндукции, возникающей даже в таких линейных провод­никах.